Лекция 2.9.1 «Неопределенный интеграл»
Учебные вопросы:
1. Первообразная функция и неопределенный интеграл
2. Основные методы интегрирования
1. Первообразная функция и неопределённый интеграл
Функция F (x) называется первообразной функцией для функции f (x) на промежутке Х, если в каждой точке х этого промежутка
F' (х)= f (x).
Например, F (x)=  является первообразной для функции f (x)= x 2, поскольку
является первообразной для функции f (x)= x 2, поскольку  .
.
Теорема. Если F 1(x) и F 2(x) – первообразные для функции f (x) в некотором промежутке Х, то найдётся такое число С, что
F 2(x)= F 1(x)+ C.
Следовательно, если F (x) – первообразная для f (x), то выражение вида F (x)+ C, где С – произвольное число, задаёт все возможные первообразные для f (x).
Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределённым интегралом от функции f(x) и обозначается

где  – символ интеграла, f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение.
– символ интеграла, f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение.
Таким образом,

где F (x) – некоторая первообразная для f (x), C – произвольная  постоянная.
постоянная. 
Пример. 
Операция нахождения неопределённого интеграла от некоторой функции называется интегрированием этой функции.
Основные свойства неопределённого интеграла:
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е.
 .
.
2. Дифференциал неопределённого интеграла равен подынтегральному выражению, т.е.
 .
.
3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
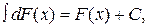
где С – произвольное число.
4. Постоянный множитель можно выносить за знак интеграла, т.е.

где  – некоторое число.
– некоторое число.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
 .
.
Основные табличные интегралы
(интегралы от основных элементарных функций):
 (1)
(1)
 (2)
(2)
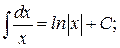 (3)
(3)
 (4)
(4)
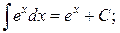 (5)
(5)
 (6)
(6)
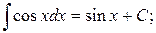 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
 (11)
(11)
Примеры:
1) 
2) 
Основные методы интегрирования
Метод замены переменной
Метод описывается формулой:

где  – функция, дифференцируемая на рассматриваемом промежутке.
– функция, дифференцируемая на рассматриваемом промежутке.
Пример.

Теорема. Пусть F (x) – некоторая первообразная для функции  Тогда
Тогда

где  и
и  – некоторые числа,
– некоторые числа,  .
.
Пример.

Интегрирование по частям
Пусть 
 – дифференцируемые функции. По свойству дифференциала
– дифференцируемые функции. По свойству дифференциала  или
или  Интегрируя левую и правую части последнего равенства, получим:
Интегрируя левую и правую части последнего равенства, получим:

Эта формула называется формулой интегрирования по частям для неопределённого интеграла. Здесь подынтегральное выражение разбивается на два сомножителя –  и
и  При этом дифференцирование может существенно упростить один из сомножителей. Если при этом интегрирование не слишком усложнит другой сомножитель, то можно упростить процесс интегрирования.
При этом дифференцирование может существенно упростить один из сомножителей. Если при этом интегрирование не слишком усложнит другой сомножитель, то можно упростить процесс интегрирования.
Пример.

В некоторых случаях интегрировать по частям приходится более одного раза.
Пример.
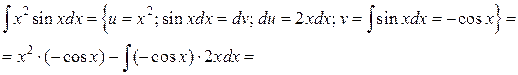

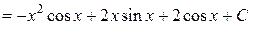 .
.
Интегрирование по частям применяется к следующим типам интегралов:
1) 
Здесь формулу применяют  раз; в первом применении
раз; в первом применении 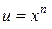 , остальные сомножители принимаются за
, остальные сомножители принимаются за  , пока степень переменной
, пока степень переменной 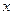 не станет равной нулю.
не станет равной нулю.
2) 
Здесь принимают  , остальные сомножители задают выражение для
, остальные сомножители задают выражение для  .
.
Пример.



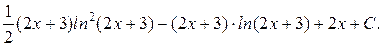
Лекция 2.9.2 «Определенный интеграл»
Учебные вопросы:
1. Определенный интеграл, его свойства и вычисление
2. Геометрические приложения определенного интеграла
3. Приближенное вычисление определенных и интегралов




