1. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры.
2. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая).
3. Предел последовательности при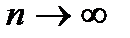 
и предел функции при 
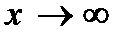. Признаки существования предела (с доказательством теоремы о пределе промежуточной функции).
4. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать).
5. Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми.
6. Второй замечательный предел, число е. Понятие о натуральных логарифмах.
7. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры.
8. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке.
9. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).
10. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
11. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции.
12. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
13. Достаточные признаки монотонности функции (один из них доказать).
14. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).
15. Достаточные признаки существования экстремума (доказать одну из теорем).
16. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимптоты. Примеры.
17. Общая схема исследования функций и построения их графиков. Пример.
18. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия.
19. Понятие об эмпирических формулах и методе наименьших квадратов. Подбор параметров линейной функции (вывод системы нормальных уравнений).
20. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.
21. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать).
22. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
23. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
24. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
25. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона–Лейбница.
26. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).
27. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
Задачи для самоподготовки
Ниже приводятся номера рекомендуемых задач с решениями и для самостоятельного выполнения по учебникам[1] [1 или 6], практикумам [2 или 7], учебнику [3] или учебникам [4 и 5], рассматриваемых в качестве основной литературы.
Студентам рекомендуется в первую очередь разобрать большинство (часть) задач с решениями (их номера выделены жирным шрифтом). Задачи для самостоятельного выполнения (их номера набраны обычным шифром) решать выборочно (в зависимости от лимита времени – например, каждую вторую задачу из списка задач по теме, или каждую третью, и т.д.).
Кроме того, уровень усвоения материала можно проверить по приводимым в практикуме [2 или 7], учебниках [3] или [4 и 5] тематическим и итоговым контрольным заданиям и тестам, решая задания в соответствии с учебно – программным материалом по каждой теме.
| Тема | Номер задач | |||
| По учебнику [1] или [6] | По практикуму [2] или [7] | По учебнику [3] | По учебнику [4]- часть 1 По учебнику [5]- часть 2 | |
| Ч а с т ь 1. Л И Н Е Й Н А Я А Л Г Е Б Р А | ||||
| РАЗДЕЛ I. Элементы матричного анализа | ||||
| 1. Матрицы и определители | 1.1 – 1.13 | 1.1 – 1.5, 1.24 – 1.27, 1.51 – –1.53 | 1.1 – 1.6, 1.8 – 1.15; 1.37 – 1.39, 1.68 – 1.70 | [4], 1.1 – 1.6, 1.8 – 1.15; 1.37 – 1.39, 1.68 – 1.70 |
| 1.14 –1.20,1.22– – 1.29 | 1.6 – 1.23, 1.29 – 1.50, 1.54 – –1.65, 1.77 – 1.84 | 1.16 –1.29, 1.40 –1.48, 1.51– – 1.57, 1.60 – 1.67, 1.71 – 1.87 | [4], 1.16 –1.29, 1.40 –1.48, 1.51– – 1.57, 1.60 – 1.67, 1.71 –1.87 | |
| 2.Системы линейных уравнений | 2.1 – 2.7, 2.10 | 2.1 – 2.4, 2.29, 2.35, 2.36 | 2.1 – 2.5, 2.8 – 2.11 | [4], 2.1 – 2.5, 2.8 – 2.11 |
| 2.11, 2.12, 2.15– 2.19, 2.21 –2.26 | 2.6 – 2.32 (четные), 2.38 – –2.48 (четные), 2.67 – 2.70, 2.72, 2.74 | 2.14 – 2.42 (четные), 2.46 – –2.49, 2.52 – 2.58 (четные), 2.62–2.77 | [4], 2.14 – 2.42 (четные), 2.46 – –2.49, 2.52 – 2.58 (четные), 2.67–2.73 | |
| 3. Векторные пространства | 3.1 – 3.3 | 3.1, 3.2, 3.24 – 3.26а, 3.29 | 3.1 – 3.3, 3.7– 3.12, 3.14– 3.17, 3.37, 3.38, 3.42 | [4], 3.1 – 3.3, 3.12– –3.16, 3.20–3.23, 3.43, 3.44, 3.69 |
| 3.14 –3.20, 3.22, 3.24, 3.26 – 3.36 | 3.5 – 3.9, 3.11, 3.14, 3.37–3.43, 3.52, 3.53, 3.130, 3.131, 3.133, 3.137a, 3.138 | 3.18, 3.19, 3.22, 3.26, 3.27, 3.30, 3.50−3.55a, 3.56, 3.57, 3.65, 3.66 | [4], 3.24, 3.25, 3.28, 3.32, 3.33, 3.36, 3.55–3.59а, 3.60, 3.61, 3.75, 3.76 | |
| РАЗДЕЛ II. Элементы аналитической геометрии | ||||
| 4. Элементы аналитической геометрии | 4.2, 4.3, 4.5 | 4.1 – 4.5, 4.7. 4.87,4.88 | 4.2, 4.3, 4.5, 4.7 – 4.11, 4.18, 4.108, 4.109 | [4], 4.2, 4.3, 4.5, 4.7 – 4.11, 4.18, 4.108, 4.109 |
| 4.15 – 4.19, 4.21 –4.24, | 4.23 – 4.26, 4.28 – 4.31, 4.34 – –4.43 | 4.36 – 4.38, 4.40 – –4.43, 4.45– 4.55, 4.114, 4.115,.117, 4.119 – 4.123 | [4], 4.36 – 4.38, 4.40 –4.43, 4.45–4.55, 4.114, 4.115, 4.117,4.119–.123 | |
| Ч а с т ь 2. М А Т Е М А Т И Ч Е С К И Й А Н А Л И З | ||||
| РАЗДЕЛ III. Введение в анализ | ||||
| 5.Функции | 5.1, 5.5 – 5.7 | 5.1, 5.4, 5.6, 5.7а | 5.1, 5.2, 5.6 – 5.8, 5.12, 5.15 | [5], 1.1, 1.2, 1.6 – 1.8, 1.12, 1.15 |
| 5.12 – 5.16, 5.22 – 5.26, 5.36, 5.37 | 5.16 – 5.19, 5.23 – 5.31, 5.46, 5.47 | [5], 1.16 – 1.19, 1.23 – 1.31, 1.46, 1.47 | ||
| 6. Пределы и непре-рывность | 6.1 – 6.3, 6.5, 6.6, 6.8 – 6.11, 6.13, 6.14 | 6.1 – 6.6, 6.12 – 6.17, 6.45, 6.46, 6.68, 6.69, 6.97 – 6.99, 6.168, 6.169 | 6.1 – 6.3, 6.5, 6.6, 6.8 – – 6.11, 6.81, 6.155 | [5], 2.1 – 2.3, 2.5, 2.6, 2.8 – – 2.11, 2.81, 2.155 |
| 6.18, 6.20 –6.27, 6.33–6.36, 6.38– 6.41 | 6.7 – 6.9, 6.11, 6.18 – 6.23, 6.25 – 6.27,6.30 –– 6.34, 6.36– – 6.39, 6.43, 6.44, 6.47 – 6.67, 6.70 – 6.96, 6.100 – 6.120, 6.170 – 6.175 | 6.12 – 6.79, 6.110 – 6.132, 6.146 – 6.153, 6.156 – – 6.165 | [5], 2.12 – 2.79, 2.110 – 2.132, 2.146 – 2.153, 2.156 – – 2.165 | |
| РАЗДЕЛ IV. Дифференциальное исчисление | ||||
| 7. Производная | 7.1 – 7.8, 7.10, 7.13, 7.15 – 7.17 | 7.1, 7.2, 7.13, 7.15, 7.109, 7.110 | 7.1 – 7.8, 7.10, 7.19 – 7.22, 7.25, 7.105, 7.106 | [5], 3.1 – 3.8, 3.10, 3.19 – 3.22, 3.25, 3.105, 3.106 |
| 7.20 – 7.29,7.35, 7.42, 7.43, 7.46– 7.49 | 7.3, 7.5 – 7.8, 7.9, 7.10, 7.21, 7.25, 7.26, 7.28 – 7.31, 7.34 – –7.37, 7.41, 7.42 – 7.46, 7.48, 7.53, 7.54, 7.113 – 7.115, 7.122 – 7.127 | 7.26–7.51, 7.64, 7.65, 7.90 – –7.100, 7.107–7.115, 7.117– – 7.119 | [5], 3.26–3.51, 3.64, 3.65, 3.90 – –3.100, 3.107–3.115, 3.117– – 3.119 | |
| 8. Приложение производной | 8.1– 8.3,8.4–8.7, 8.9, 8.11 – 8.15, 8.17 | 8.1, 8.9, 8.10, 8.13, 8.14, 8.35, 8.36, 8.38 – 8.40, 8.94 – 8.97 | 8.1 – 8.8, 8.10, 8.12 – 8.17, 8.25, 8.26, 8.28 – 8.30, 8.51, 8.52, 8.54 – 8.56, 8.110 – –8.113 | [5], 4.1 – 4.8, 4.10, 4.12 – 4.17, 4.25, 4.26, 4.28 – 4.30, 4.51, 4.52, 4.54 – 4.56, 4.110 – –4.113 |
| 8.19–8.34, 8.41– 8.53 | 8.4 – 8.6, 8.15 – 8.22, 8.25, 8.27 – 8.30, 8.41, 8.52, 8.55 – –8.57,8.69 – 8.71, 8.75 – 8.77, 8.100 – 8.102, 8.105, 8.106, 8.108 – 8.118, 8.120, 8.121, 8.123, 8.124 | 8.20–8.23, 8.31 – 8.38, 8.41, 8.43–8.46,8.57–8.73, 8.75, 8.77 – 8.79, 8.81, 8.82,8.84 – –8.87, 8.89, 8.91– 8.94, 8.116 – 8.118, 8.121, 8.122, 8.124 – 8.134, 8.136, 8.137, 8.139, 8.140 | [5], 4.20–4.23, 4.31 – 4.38, 4.41, 4.43–4.46,4.57–4.73, 4.75, 4.77 – 4.79, 4.81, 4.82,4.84 – –4.87, 4.89, 4.91– 4.94, 4.116 – 4.118, 4.121, 4.122, 4.124 – 4.134, 4.136, 4.137, 4.139, 4.140 | |
| 9. Дифференциал функции | 9.1, 9.3, 9.5 | 9.1, 9.2, 9.6 | 7.12 – 7.14, 7.16, 7.120 | [5], 3.12 – 3.14, 3.16, 3.120 |
| 9.6 – 9.12 | 9.7 – 9.12, 9.13 – 9.17 | 7.122 – 7.125, 7.127, 7.128, 7.130, 7.132, 7.134 – 7.138, 7.140, 7.141 | 3.122 – 3.125, 3.127, 3.128, 3.130, 3.132, 3.134 – 3.138, 3.140, 3.141 | |
| 10. Функция нескольких переменных | 15.7, 15.9, 15.13 | 15.1 – 15.3, 15.27, 15.88 – –15.90 | 9.1, 9.2, 9.6 – 9.9, 9.13 – – 9.15, 9.40, 9.41, 9.69 – – 9.71, 9.101 – 9.103 | [5], 5.1, 5.2, 5.6 – 5.9, 5.13 – – 5.15, 5.40, 5.41, 5.69 – – 5.71, 5.101 – 5.103 |
| 15.23 – 15.32, 15.39, 15.40 | 15.6 –15.11,15.14–15.19, 15.31, 15.33–15.36, 15.38, 15.91 – 15.98 | 9.19 – 9.24, 9.44–9.51, 9.75– – 9.78, 9.80 – 9.88, 9.104 – – 9.109 | [5], 5.19 – 5.24, 5.44–5.51, 5.75– – 5.78, 5.80 – 5.88, 5.104 – – 5.109 | |
| РАЗДЕЛ V. Интегральное исчисление и дифференциальные уравнения | ||||
| 11. Неопределенный интеграл | 10.1–10.4,10.6 – – 10.11, 10.13, 10.14, 10.18а, 10.23, 10.24а, 10.25 – 10.27 | 10.1, 10.19, 10.20, 10.73, 10.105, 10.106, 10.132 | 10.1 – 10.4, 10.6 – 10.8, 10.10, 10.12 – 10.14, 10.19, 10.41, 10.42, 10.95, 10.155 | [5], 6.1 – 6.4, 6.6 – 6.8, 6.10, 6.12 – 6.14, 6.19, 6.41, 6.42, 6.95, 6.155 |
| 10.33 – 10.39, 10.41 – 10.45, 10.47 – 10.54, 10.56 – 10.59, 10.61, 10.63 – – 10.65, 10.68 – – 10.70 | 10.2 – 10.4, 10.6 – 10.10, 10.13 – 10.15, 10.18, 10.21, 10.22, 10.24, 10.25, 10.28 – – 10.34,10.37,10.38,10.42– –10.56, 10.58 – 10.65, 10.75 – 10.81, 10.84, 10.85, 10.92, 10.93, 10.96, 10.103, 10.104, 10.107, 10.116,10.117, 10.133, 10.135 –10.136, 10.138, 10.140, 10.141 | 10.20 – 10.22, 10.24 – 10.32, 10.35 – 10.37, 10.43, 10.44, 10.46,10.47,10.50–10.56, 10.59, 10.60, 10.64 – 10.78, 10.80–10.87,10.97 – 10.107, 10.114,10.115,10.118,10.125 – 10.126, 10.156 – 10.161, 10.163 – 10.167 | [5], 6.20 – 6.22, 6.24 – 6.32, 6.35 – 6.37, 6.43, 6.44, 6.46,6.47,6.50–6.56, 6.59, 6.60, 6.64 – 6.78, 6.80–[5], [5], 6.87,6.97 – 6.107, 6.114,6.115,6.118,6.125, 6.126, 6.156 – 6.161, 6.163 – 6.167 | |
| 12. Определенный интеграл | 11.1–11.7,11.10, 11.11, 11.18 ––11.22 | 11.1, 11.30, 11.73, 11.91 | 11.1 – 11.7,11.13, 11.14, 11.16, 11.23, 11.55, 11.112, 11.136 | [5], 7.1 – 7.7, 7.13, 7.14, 7.16, 7.23, 7.55, 7.112, 7.136 |
| 11.25 – 11.30, 11.32 – 11.35, 11.37 – 11.39, 11.41 – 11.52, 11.57, 11.59 | 11.2 – 11.12, 11.14, 11.21, 11.22, 11.25, 11.26, 11.27, 11.29, 11.36 – 11.41, 11.43 – –11.45, 11.47 – 11.51, 11.75, 11.76 – 11.78, 11.81, 11.82, 11.92, 11.93 – 11.95 | 11.24 – 11.38, 11.40, 11.47, 11.48, 11.51 – 11.53, 11.55а, 11.61 – 11.66, 11.68 – 11.80, 11.82 – 11.86, 11.114 – –11.124, 11.126, 11.127, 11.133, 11.137 – 11.140 | [5], 7.24 – 7.38, 7.40, 7.47, 7.48, 7.51 – 7.53, 7.55а, 7.61 – 7.66, 7.68 – 7.80, 7.82 – 7.86, 7.114 – 7.124, 7.126, 7.127, 7.133, 7.137 – 7.140 |
