Теорема Ролля* и Лагранжа. Правило Лопиталя (без вывода). Признаки возрастания и убывания функции. Экстремум функции. Необходимые и достаточные признаки экстремума (второй достаточный признак – без доказательства). Наибольшее и наименьшее значения функции на отрезке; их нахождение; решение задач. Исследование функции (область определения, четность и нечетность, интервалы монотонности и точки экстремума, поведение функции при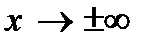 
и в точках разрыва, вертикальные, горизонтальные и наклонные асимптоты, точки пересечения графика с осями координат) и построение ее графика. Квадратичная функция y = ax2 + bx + c и ее график. Дробно-линейная функция y = (ax + b)/(cx + d) и ее график ([1 или 6, § 8.1 – 8.5, 8.7 – 8.9]; [2 или 7, § 8.1 – 8.3, 8.5], или [3, § 8.1 – 8.5, 8.7, 8.8, 8.10 – 8.12, 8.14], или [5, §4.1 – 4.5, 4.7, 4.8, 4.10 – 4.12, 4.14])
Одно из простейших приложений производной – раскрытие неопределенностей вида [0/0] или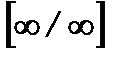 
с помощью правила Лопиталя ([1, или 6, или 3, § 8.2]). Обратите внимание на то, что согласно формуле (8.3) предел отношения двух бесконечно малых или двух бесконечно больших функций равен пределу отношения их производных, а не пределу производной частного этих функций.
Теоремы дифференциального исчисления являются обоснованием такой важной области приложения производных, как исследование функций. Студенты должны знать формулировки этих теорем, четко различая в них условие и заключение.
В учебнике приведена схема исследования функции для нахождения ее характерных точек и особенностей, по которым можно построить ее график ([1, или 6, или 3, § 8.8]). Выполнение пункта 60 этой схемы, связанного с нахождением интервалов выпуклости функции и точек перегиба, не обязательно.
Тема 9. Дифференциал функции
Понятие дифференциала функции. Геометрический смысл дифференциала. Свойства дифференциала. Инвариантность формы дифференциала первого порядка. ([1или 6, § 9.1, 9.2]; [2 или 7, гл. 9]; [3, § 7.7 – 7.9, 7.13] или [5, §3.7 – 3.9, 3.13]).
Дифференциал функции y = f (x) – главная, линейная (относительно приращения Δ x аргумента) часть приращения функции – равен произведению производной на дифференциал независимой переменной, т.е. dy =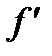 
(x) dx. Геометрический смысл дифференциала рассмотрен в ([1 или 6, § 9.1] или [3, § 7.4]).
Операция нахождения дифференциала сводится к нахождению производной и также называется дифференцированием функции.
Важное свойство дифференциала первого порядка – инвариантность его формы (или формулы). Это означает, что дифференциал функции
y = f (u) есть dy =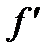 
(u) du и не зависит от того, является ли u независимой переменной или функцией. Свойство инвариантности формы дифференциала используется далее в интегральном исчислении.
