Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла (с доказательством). Таблица основных интегралов. Интегрирование методом разложения, замены переменной и по частям. Понятие о «неберущихся» интегралах ([1 или 6, § 10.1 – 10.5, 10.8]; [2 или 6, § 10.1 – 10.3, 10.5], или [3, § 10.1 – 10.6, 10.9 – 10.11], или [5, §6.1 – 6.6, 6.9 – 6.11]).
Следует обратить внимание на то, что интегрирование вводится как операция, обратная дифференцированию, но в отличие от последнего приводит к неоднозначному результату: для любой непрерывной функции f (x) имеется бесконечное множество первообразных. Они отличаются друг от друга лишь на постоянное слагаемое.
Доказательства основных свойств неопределенного интеграла получены исходя из определения первообразной. Правильность интегрирования можно проверить дифференцированием; этот прием следует использовать для проверки решения соответствующих примеров в контрольной работе.
Под непосредственным интегрированием понимают нахождение неопределенного интеграла путем преобразования его к табличному с помощью основных правил интегрирования и тождественных преобразований подынтегральной функции.
Обратите внимание на свойство, связанное с линейным преобразованием аргумента ([1 или 6, формула (10.17)] или [3, формула (10.19)]), так как это простейшее из свойств, которое часто применяется при непосредственном интегрировании. Используя его, можно свести к табличным ряд интегралов.
Метод подстановки, или метод замены переменной, – один из основных приемов интегрирования функций. Следует обратить внимание на то, что можно использовать подстановки двух видов:
а) переменная интегрирования x заменяется функцией переменной t:
 а
а  ‒
‒
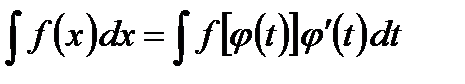 ;
;
б) новая переменная t вводится как функция переменной интегрирования x: 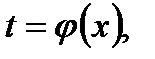
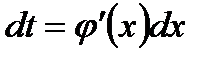 ‒
‒
 .
.
Последнюю подстановку удобно применять, если подынтегральное выражение содержит дифференциал (производную) функции  с точностью до постоянного множителя.
с точностью до постоянного множителя.
Если интеграл, полученный после замены переменной, стал «проще» данного (преобразован в табличный или приводящийся к табличному), то цель подстановки достигнута.
После интегрирования функции по переменной t необходимо вернуться к прежней переменной x, выразив t через x по формуле, применявшейся при подстановке.
Примеры различных подстановок даны в ([1, или 6, или 3, § 10.3, 10.6]).
Практическое применение формулы интегрирования по частям ([1 или 6, или 3, § 10.4]), если оно целесообразно, связано с проблемой правильного разбиения подынтегрального выражения на сомножители u и dv. Отметим, что формулу интегрирования по частям, как правило, удобно применять, если подынтегральная функция является произведением многочлена на показательную или логарифмическую функцию ([1 или 6, примеры 10.10 – 10.13]; [3, примеры 10.8, 10.9]).






