Функцияның туындысы. Анықтама. Функция өсімшесі  -тің аргумент өсімшесі
-тің аргумент өсімшесі  -ке катынасының
-ке катынасының  нөлге ұмтылғандағы шегі бар болса, онда оны
нөлге ұмтылғандағы шегі бар болса, онда оны  функциясының х0 нүктедегі туындысы деп атайды, яғни
функциясының х0 нүктедегі туындысы деп атайды, яғни  .
.
Функцияның қандайда бір аралықтың кез келген нүктесінде туындысы болса, онда оны осы аралықта дифференциалданады дейді.  функциясының
функциясының 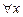 нүктедегі туындысы мынандай символдармен белгіленеді:
нүктедегі туындысы мынандай символдармен белгіленеді:  .
.
Егер аргумент х-ке әртүрлі мәндер берсек, онда  -те әртүрлі мәндер қабылдайды, сондықтан функция туындысын х-тің функциясы деп карастыруға болады.
-те әртүрлі мәндер қабылдайды, сондықтан функция туындысын х-тің функциясы деп карастыруға болады.
Туындының геометриялық мағынасы:  функциясының х0 нүктедегі туындысы функцияның графигіне
функциясының х0 нүктедегі туындысы функцияның графигіне  нүктеде жүргізілген жанаманың бұрыштық коэффициентіне тең, яғни
нүктеде жүргізілген жанаманың бұрыштық коэффициентіне тең, яғни  ,
,  ,
,  .
.  функциясының графигіне оның
функциясының графигіне оның  нүктесінде жүргізілген жанаманың теңдеуі:
нүктесінде жүргізілген жанаманың теңдеуі:  , ал оған осы нүктеде перпендикуляр болатын түзу (нормаль) теңдеуі:
, ал оған осы нүктеде перпендикуляр болатын түзу (нормаль) теңдеуі:  болады.
болады.
Туындының физикалык мағынасы:  функциясының х0 нүктедегі туындысы осы нүктедегі функцияның х аргументіне қатысты өзгеру жылдамдығын анықтайды.
функциясының х0 нүктедегі туындысы осы нүктедегі функцияның х аргументіне қатысты өзгеру жылдамдығын анықтайды.
Теорема (функция туындысының бар болуының кажетті шарты). Егер  функциясы х=х0 нүктеде дифференциалданатын болса, онда ол осы нүктеде үзіліссіз.
функциясы х=х0 нүктеде дифференциалданатын болса, онда ол осы нүктеде үзіліссіз.
Мысалы, 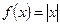 функциясы
функциясы  нүктеде үзіліссіз болғанмен де оның осы нүктеде туындысы жоқ. Өйткені,
нүктеде үзіліссіз болғанмен де оның осы нүктеде туындысы жоқ. Өйткені,  ,
, 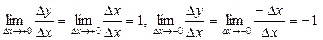 . Яғни
. Яғни  нүктеде оң және сол жақты шектер тең емес.
нүктеде оң және сол жақты шектер тең емес.
Туындының анықтамасын пайдаланып элементар функциялардың туындылар кестесі жасалған:
1. 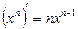 , ,  2.
2.  3.
3.  4.
4.  5.
5. 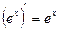 6.
6. 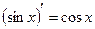 7.
7. 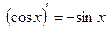 8.
8.  9.
9. 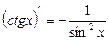
| 10. 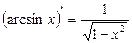 11.
11.  12.
12. 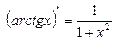 13.
13.  14.
14.  15.
15.  16.
16.  17.
17. 
|
Теорема. Егер 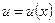 ,
,  функциялары
функциялары  сегментінде дифференциалданса және С -тұрақты шама болса, онда төмендегідей негізгі дифференциалдау ережелері орындалады:
сегментінде дифференциалданса және С -тұрақты шама болса, онда төмендегідей негізгі дифференциалдау ережелері орындалады:
1.Тұрақты шаманың туындысы 0-ге тең:  2.
2. 
3. 
 4.
4. 
5.  6.
6. 

Күрделі функцияның туындысы. Анықтама. Егер  , ал
, ал  , яғни
, яғни  -тің мәндерінің жиыны
-тің мәндерінің жиыны  функциясының анықталу облысының ішкі жиыны болса, онда
функциясының анықталу облысының ішкі жиыны болса, онда  айнымалы х бойынша күрделі функция болып саналады. Мұндағы
айнымалы х бойынша күрделі функция болып саналады. Мұндағы 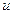 аралық аргумент деп аталады.
аралық аргумент деп аталады.  және
және  функцияларының суперпозициясы немесе функцияның функциясы деп аталады.
функцияларының суперпозициясы немесе функцияның функциясы деп аталады.
 -күрделі функцияның туындысы сол функцияның аралық аргумент бойынша алынған туындысын аралық аргументтің туындысына көбейткенге тең болады, яғни
-күрделі функцияның туындысы сол функцияның аралық аргумент бойынша алынған туындысын аралық аргументтің туындысына көбейткенге тең болады, яғни
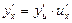 немесе
немесе 
Егер күрделі функция  екі
екі 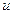 және
және  аралық аргументтері бойынша жасалса:
аралық аргументтері бойынша жасалса:  ,
,  ,
,  , яғни
, яғни  , онда оның туындысы:
, онда оның туындысы:  .
.
Мысал. 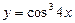 ,
, 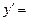 ?
?
Шешуі: 
Айқындалмаған функцияның туындысы. 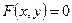 теңдеулерімен берілген, яғни х аргументі мен у функциясының арасындағы байланыс у -ке қатысты шешіле бермейтін түрде берілген функцияны айқындалмаған функция деп атайды. Оның туындысын табу үшін у -ті х -тің функциясы деп қарастырып, теңдеуден х бойынша туынды аламыз да, шыққан теңдеуден
теңдеулерімен берілген, яғни х аргументі мен у функциясының арасындағы байланыс у -ке қатысты шешіле бермейтін түрде берілген функцияны айқындалмаған функция деп атайды. Оның туындысын табу үшін у -ті х -тің функциясы деп қарастырып, теңдеуден х бойынша туынды аламыз да, шыққан теңдеуден  -ты табамыз.
-ты табамыз.
Параметрлік түрде берілген функцияның туындысы. х аргументі мен у функциясының арасындағы байланыс  -параметріне қатысты теңдеулермен берілсе:
-параметріне қатысты теңдеулермен берілсе:  ,
, 
 , онда функция параметрлік түрде берілген функция деп аталады. Бұл теңдеуді х0у жазықтығында қозғалып бара жатқан нүкте координаталарының
, онда функция параметрлік түрде берілген функция деп аталады. Бұл теңдеуді х0у жазықтығында қозғалып бара жатқан нүкте координаталарының  уақытына тәуелділігі деп қарастыруға болады, яғни
уақытына тәуелділігі деп қарастыруға болады, яғни  функциясының графигі қозғалмалы нүктенің траекториясын көрсетеді.
функциясының графигі қозғалмалы нүктенің траекториясын көрсетеді.
 ,
, 
 функцияларының
функцияларының  параметрі бойынша туындылары бар және
параметрі бойынша туындылары бар және  болсын. Сонда, бірінші туындысы:
болсын. Сонда, бірінші туындысы:  , ал екінші туындысы:
, ал екінші туындысы: 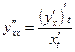 формулаларымен табылады.
формулаларымен табылады.
Мысал. 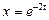 ,
,  .
.  ,
,  =?
=?
Шешуі.  ,
, 
 .
.  .
.
Кері функцияның туындысы. Егер  сегментінде
сегментінде  үзіліссіз, бірсарынды және нөлге тең емес туындысы бар функция болса, онда оның
үзіліссіз, бірсарынды және нөлге тең емес туындысы бар функция болса, онда оның 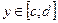 сегментінде
сегментінде 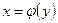 керіфункциясы үзіліссіз, бірсарынды және туындысы:
керіфункциясы үзіліссіз, бірсарынды және туындысы:  немесе
немесе  бар болады. Сонымен, кері функцияның туындысы тура функция туындысының кері шамасына тең болады.
бар болады. Сонымен, кері функцияның туындысы тура функция туындысының кері шамасына тең болады.
Мысал.  ,
,  ,
,  =? Шешуі:
=? Шешуі:  ,
,  ,
,
 ,
,  .
. 
Логарифмдік дифференциалдау әдісі.  түріндегі функцияны дәрежелі-көрсеткіштік функция дейміз. Мысалы,
түріндегі функцияны дәрежелі-көрсеткіштік функция дейміз. Мысалы, 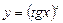 ,
,  ,
,  және т.б. Мұндай түрдегі функцияның туындысын табу үшін логарифмдік дифференциалдау әдісін қолданамыз. Ол үшін
және т.б. Мұндай түрдегі функцияның туындысын табу үшін логарифмдік дифференциалдау әдісін қолданамыз. Ол үшін 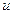 және
және 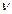 функцияларының х нүктесінде туындысы бар және
функцияларының х нүктесінде туындысы бар және 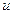 функциясы х-тің белгілі бір маңайында оң деп ұйғарамыз. Сосын, теңдіктің екі жағын да логарифмдеп, логарифм қасиеттерін пайдалансақ:
функциясы х-тің белгілі бір маңайында оң деп ұйғарамыз. Сосын, теңдіктің екі жағын да логарифмдеп, логарифм қасиеттерін пайдалансақ:  болады. Бұл теңдіктен күрделі функцияның туындысын табу ережесін колданып туынды табамыз:
болады. Бұл теңдіктен күрделі функцияның туындысын табу ережесін колданып туынды табамыз:  . Осы теңдеуден у'- тітапсақ, мынадай теңдікті аламыз:
. Осы теңдеуден у'- тітапсақ, мынадай теңдікті аламыз:
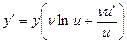 . Сонымен,
. Сонымен, 
Немесе, негізгі логарифмдік теңбе-теңдікті: 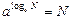 пайдаланып, дәрежелі-көрсеткіштік функцияны мынадай күрделі көрсеткіштік фукцияға келтіреміз де:
пайдаланып, дәрежелі-көрсеткіштік функцияны мынадай күрделі көрсеткіштік фукцияға келтіреміз де: 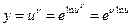 , осы күрделі функциядан туынды табамыз.
, осы күрделі функциядан туынды табамыз.
1-мысал.  функциясының туындысын табу керек.
функциясының туындысын табу керек.
Шешуі: 1-тәсіл: 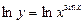 ,
,  .
.
 Яғни,
Яғни, 
2-тәсіл. 

Сонымен қатар, логарифмдік дифференциалдау әдісі функцияның туындысын табуды жеңілдету үшін де қолданылады.
Функцияның дифференциалы.  функциясының х нүктесінде туындысы бар болсын, яғни
функциясының х нүктесінде туындысы бар болсын, яғни  . Бұдан,
. Бұдан,  , мұндағы
, мұндағы  жоғарғы ретті шексіз аз функция, сондықтан
жоғарғы ретті шексіз аз функция, сондықтан 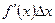 функция өсімшесінің басты бөлігі деп аталады.
функция өсімшесінің басты бөлігі деп аталады.
Анықтама.  функциясының х нүктесіндегі дифференциалы деп функция өсімшесінің басты бөлігін айтады және оны
функциясының х нүктесіндегі дифференциалы деп функция өсімшесінің басты бөлігін айтады және оны  немесе
немесе 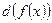 деп белгілейді:
деп белгілейді: 
 ,
,  . Ендеше,
. Ендеше, 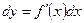 , бұдан
, бұдан  .
.
Теорема.  функциясының х нүктесінде дифференциалы болу үшін оның туындысының бар болуы қажетті және жеткілікті.
функциясының х нүктесінде дифференциалы болу үшін оның туындысының бар болуы қажетті және жеткілікті.
Дифференциалдың геометриялық мағынасы:  функциясының х нүктесінде дифференциалы функция графигіне сол нүктеде жүргізілген жанама ординатасының өсімшесіне тең болады.
функциясының х нүктесінде дифференциалы функция графигіне сол нүктеде жүргізілген жанама ординатасының өсімшесіне тең болады.  , сондықтан
, сондықтан 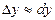 немесе
немесе 
 . Бұл теңдік функцияның жуық мәндерін табу үшін қолданылады.
. Бұл теңдік функцияның жуық мәндерін табу үшін қолданылады.
Дифференциал табу ережелері туынды табу ережелерінен шығады:
1.  , 2.
, 2. 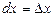 , егер х-тәуелсіз айнымалы болса;
, егер х-тәуелсіз айнымалы болса;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6. 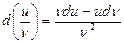 ,
, 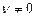
7.  . Бұл ереже дифференциал түрінің инварианттылығы деп аталады.
. Бұл ереже дифференциал түрінің инварианттылығы деп аталады.
Мысал.  функциясының дифференциалын табыңыз.
функциясының дифференциалын табыңыз.
Шешуі: 






