Екінші ретті қисықтар. Екінші дәрежелі алгебралық теңдеулермен өрнектелетін қисықтарды екінші ретті қисықтар деп атайды. 1) Шеңбер. Анықтама. Центр деп аталатын берілген нүктеден бірдей қашықтықта жататын нүктелердің геометриялық орнын шеңбер деп атайды.
шартынан центрі 
нүктесі, радиусы 
болатын шеңбердің теңдеуін аламыз: 
, яғни 
. Егер 
болса, онда:
.
2) Эллипс. Анықтама. Координат өстерінің бірінде берілген фокустар деп аталатын екі нүктеден ара қашықтықтарының қосындысы әрқашанда тұрақты шама болатын нүктелердің геометриялық орындарын эллипс дейміз (1-сурет).
1-сурет 2-сурет 3-сурет
Анықтама бойынша: 
-фокустары. 
-фокальдық радиустар. 
. Бұдан 
деп белгілесек, эллипстің ықшам теңдеуі шығады: 
, 
.
Эллипс формасы 
қатынасымен анықталады, бұл қатынас эксцентриситет деп аталады, яғни 
. 
. 
; 
. 
түзулері – директрисалары.
- үлкен өс,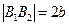 
-кіші өс.
Егер 
болса, онда оның үлкен өсі- 
, кіші өсі- 
, 
фокустары ОУ өсінде жатады. 
болады.
3) Гипербола. Анықтама.Координат өстерінің бірінде берілген фокустар деп аталатын екі нүктеден арақашықтықтарының айырымы әрқашанда тұрақты шама болатын нүктелердің геометриялық орындарын гипербола дейміз. (Тұрақты шама фокустардың арақашықтығынан кіші, 
) (2-сурет).
Анықтама бойынша: 
немесе 
, яғни 
. Осы теңдеуге түрлендіру жасасақ, 
, 
. -нақты өс, - жорамал өс. - эксцентриситеті, 
, өйткені 
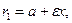
. Фокальдық радиустары: оң тармақ үшін: 
. Сол тармақ үшін: 
. 
.
- нақты өсі ОУ, жорамал өсі ОХ болатын гипербола. 
.
Анықтама. Координат жүйесінің бас нүктесінен өтетін және гипербола тармақтарымен шексіз алыстағы нүктелерде кездесетін түзуді асимптота дейді: 
.
4) Парабола. Анықтама.Фокус депаталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын жазықтықтағы нүктелердің геометриялық орындарын парабола деп атайды (3-сурет).
Анықтама бойынша: 
. 
; Бұдан: 
. 
= 
. 
. Парабола түрлері: 
болғанда, 
аралығында өзгереді, ОХ - симметрия өсі, төбесі - 
нүктесі, 
- фокусы, 
түзуі-директрисасы. 
теңдеулері төбесі координат жүйесінің бас нүктесі болатын, 
өсіне қарағанда симметриялы параболаларды анықтайды.
Екінші ретті қисықтардың ортақ қасиеті: олардың қай-қайсысының да бір кез келген нүктесінің берілген нүкте (фокус) мен берілген түзуден (директриса) қашықтықтарының қатынасы тұрақты шама және ол эксцентриситетке тең болады: 
.
Жазықтықтағы екінші ретті қисықтың жалпы теңдеуі мына түрде беріледі:
Мұндағы 
- тұрақты шамалар және 
коэффициенттері бір мезгілде нөлге тең емес.
Координат жүйесін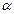 
бұрышқа бұру арқылы екінші ретті қисықтың бес мүшелі теңдеуін алуға болады: 
Бұл теңдеу: 1) 
болғанда эллипсті (нақты, жорамал немесе нүктеге айналатын); 2) 
болғанда шеңберді (нақты, жорамал немесе нүктеге айналатын); 3)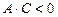 
болғанда гиперболаны немесе қиылысатын түзулер жұбын; 4) 
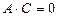болғанда параболаны немесе параллель түзулер жұбын анықтайды.
Егер кейбір түрлендіру (мысалы, толық квадратқа келтіру) жалпы теңдеуді мына түрге өрнектесе: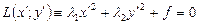 
онда соңғы теңдеу қисықтың ықшам (канонды) теңдеуі деп аталады, мұндағы 
- кез келген сандар.
Мысал. Берілген теңдеу қандай қисықты анықтайды: 
?
Шешуі. Түрлендіру жасаймыз: 
; 
Координат өстерін бас нүктесі 
болатындай параллель көшіреміз: 
. Бұдан: 
. Сонда жаңа өстерге байланысты қисықтың теңдеуі мына түрге келеді: 
. Бұл эллипстің канонды теңдеуі, оның жарты өстері: 
.
Екінші ретті беттер. Кеңістікте екінші ретті беттер екінші дәрежелі алгебралық теңдеулермен анықталады, яғни олардың жалпы теңдеуі: 
, мұндағы коээфициенттері бір мезгілде нөлге тең емес, 
-тұрақты шамалар, 
беттің кез келген нүктесінің координаттары. Осы шамалардың әртүрлі мәндеріне сәйкес бұл теңдеу әртүрлі беттерді анықтайды. Бұл теңдеу, сонымен қатар, екі жазықтықтың жиынын, нүктені, түзуді анықтауы да немесе ешқандай геометриялық кескінді анықтамауы да мүмкін (бос жиын немесе «жалған» бетті).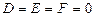 
болғанда жалпы теңдеуден: 
толық квадратқа келтіру, координат өстерін параллель көшіру арқылы беттің әртүрлі ықшам (канонды) теңдеулері алынады.
1. Сфера беті. Анықтама. Кеңістікте берілген нүктеден бірдей қашықтықта орналасқан нүктелердің геометриялық орнын сфералық немесе шар беті деп атайды. 
, мұндағы 
-сфера центрінің координаттары, ал -оның радиусы. Егер 
болса, онда: 
. 
-тың таңбасы оң болса, сфералық бет нақты, егер теріс болса жорамал, ал 
болса, теңдеу бір ғана нүктені анықтайтын болады.
2. Цилиндрлік беттер. Анықтама. Берілген 
сызығын қиятын және берілген 
түзуіне параллель түзулерден тұратын бетті цилиндрлік бет деп атайды. Мұндағы сызығы цилиндрдің бағыттаушысы, ал түзуіне параллель түзулер оның жасаушысы деп аталады.
Цилиндр қималарының түріне қарай төртке бөлінеді: дөңгелек, эллипстік, гиперболалық және параболалық. Олар декарт координаталар жүйесінде мынандай теңдеулермен беріледі: 
(4-сурет), 
(6-сурет), (5-сурет).
3. Конустық беттер. Анықтама. Берілген 
нүктеден өтіп берілген сызығымен қиылысатын түзулерден тұратын бетті конустық бет немесе конус деп атайды. Мұндағы берілген нүкте конустың төбесі, сызығы бағыттаушысы, ал бетті құрайтын түзулерді оның жасаушысы деп атайды.
- координат жүйесінің бас нүктесінен өтіп, ОZ өсіне симметриялы болатын екінші ретті конустың теңдеуі (9-сурет).
4. Айналу беттері. Анықтама. Берілген сызығы тағайындалған 
өсі бойымен айналу нәтижесінде пайда болған бетті айналу беті деп атайды. Айналатын сызықтың түріне байланысты бет те әртүрлі болады. Мысалы, егер шеңбер өзінің диаметрінен айналса, сфералық бет, ал координат бас нүктесінен өтетін түзу 
өсін айналса, дөңгелек конус пайда болады.
Берілген сызығының қайсыбір өсті айналуынан шығатын беттің теңдеуін алу үшін мынандай ереже бар: сызығының теңдеулерінің (кеңістіктегі сызық екі беттің қиылысуы ретінде анықталатын болғандықтан) екіншісінде айналу өсіне сәйкес координатты өзгеріссіз қалдырып, ал екінші координатты айналу өсінен басқа қалған екі өске сәйкес координаттардың квадраттарының қосындысының квадрат түбіріне ауыстыру керек. Мысалы, 
жазықтығында жатқан сызығы 
теңдеуімен берілсе және ол өсін айналса, онда айналудан шыққан бет теңдеуі: 
болады. Осы ереже арқылы екінші ретті қисықтардың айналуынан шығатын беттердің теңдеулерін аламыз.
1) Эллипсоид: 
(10-сурет).
2) Бір қуысты гиперболоид: 
(11-сурет).
3) Қос қуысты гиперболоид: 
(12-сурет).
4) Эллиптикалық параболоид: 
(7-сурет).
5) Гиперболалық параболоид: 
(8-сурет).
Беттердің берілген теңдеуі бойынша оның геометриялық түрін анықтау үшін қима әдісі қолданылады. Яғни, 2-нші ретті бетті координат жазықтықтарымен немесе оларға параллель жазықтықтармен қиямыз да, қимада пайда болатын сызықтарды зерттейміз. Қимада пайда болған сызықтар осы беттің геометриялық түрін анықтайды.
4-сурет 5-сурет 6-сурет
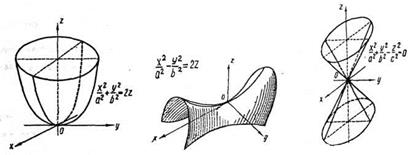
7-сурет 8-сурет 9-сурет
10-сурет 11-сурет 12-сурет
Бақылау сұрақтары:
1. Қисықтар мен беттердің реті дегеніміз не?
2. Екінші ретті қисықтарға ортақ қасиеті қандай?
3. Екінші ретті беттердің қандай түрлері бар?
Негізгі әдебиет: [4], 3 тарау, § 3.1-3.32, 5 тарау, § 5.1-5.10 (110-152, 218-252 беттер).
Қосымша әдебиет: [17], 2 тарау, § 2.11-2.16, 2.22-2.26 (85-102, 118-131 беттер).
