Бірнеше айнымалылар функциялары туралы негізгі ұғымдар. Біз осы уақытқа дейін жоғарғы математика курсында анықталу облысы мен мәндер облысы сандар өсінің кейбір ішкі жиындары болып келген бір айнымалы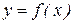 
функциясын қарастырдық. Бірақ практикада айнымалысы бір аргументтен асатын өзінің зерттеу ерекшеліктері бар функциялар кеңінен қолданылады.
Анықтама. Екі (үш) айнымалы функция деп, анықталу облысы жазықтықтағы (кеңістіктегі) кейбір ішкіжиындар қурайтын, ал мәндер облысы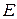 
нақты сандар осіне жататын, функцияны айтады.
Егер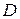 
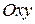жазықтығында ал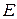 
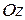өсінде жатса онда екі айнымалы функцияны мына
түрде жазамыз. Егер 
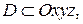ал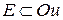 
, онда үш айнымалы функцияны мына түрде 
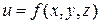жазамыз.
Анықтама. Радиусы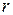 
-ге тең жазықтықтағы 
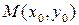(немесе кеңістіктегі 
) нүктесінің аймағы деп центрі 
нүктесіндегі радиусы 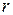-ге тең шеңберсіз дөңгелекті (немесе сфеарасыз шарды) айтады.
Мұндай аймақты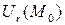 
арқылы белгілейміз. Жазықтықта 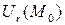мына теңсіздігімен анықталады: 
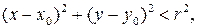ал кеңістікте
.
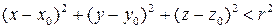Анықтама. Егер нүктесінің радиусы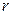 
-ге тең кез келген аймағы 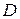жиынымен және оның толықтауыш жиынымен қиылысатын болса, онда нүктесі 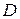жиынының шекаралық нүктесі деп аталады.
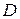жиынының барлық шекаралық нүктелері осы жиынның шекарасы деп аталады және 
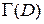деп белгіленеді.
Анықтама. 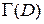шекарасын қамтитын 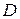жиынын жабық (тұйық) жиын деп атаймыз. Бірде – бір шекаралық нүктесін қамтымайтын 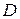жиыны ашық жиын деп аталады.
1-мысал. 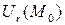аймағы өз шекарасының бірде – бір нүктесін қамтымайды – шеңберді (немесе сфераны), сондықтан 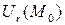– ашық жиын.
2-мысал.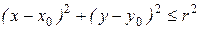 
теңсіздігімен жазықтықта берілген дөңгелек өз шекарасын – шеңберді қамтиды: 
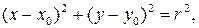сондықтан ол – жабық жиын.
3-мысал. Жазықтықтың ширегі мына теңсіздіктермен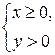 
анықталған және 
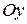өсіндегі шекаралық бөлігін қамтиды және 
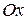осінде шекараның бөлігін қамтымайды. Бұл жиын ашық та, жабық та емес.
– сан болсын. функциясының деңгей сызығы деп, координаталары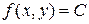 
теңдігін қанағаттандыратын 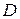анықталу облысындағы барлық 
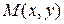нүктелер жиынын айтамыз.
Осы сияқты географиядағы биіктіктері бірдей сызықтар бейнеленеді. Олар теңіз деңгейінен жергілікті нүктенің биіктігін анықтайтын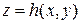 
функциясының деңгей сызықтары болады.
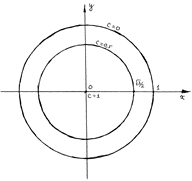
4-мысал.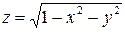 
функциясының әртүрлі деңгей сызықтарын табайық. Мұндай сызықтар 
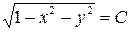теңдеуімен анықталады. 
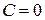болғанда 
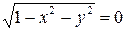аламыз;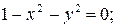 
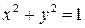. Сондықтан 
-дік деңгейде сызық центрі координаталар бас нүктесіндегі радиусы 1-ге тең шеңбер болады.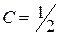 
болғанда аламыз:
; 
; 
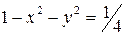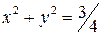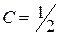. деңгейдегі сызықтық радиусы 
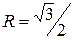-ге тең центрі координаталар бас нүктесіндегі шеңбер болады. 
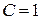болғанда 
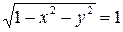теңдеуі 
нүктесін, координаталар басын анықтайды:
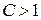және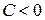 
болғанда 
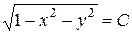шешулері болмайды, сондықтан берілген функцияның деңгейлік сызықтары жоқ. Үш айнымалы функция графигінің орнына келесі ұғымдарды пайдалануға болады. 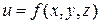функциясының деңгей сызықтары деп координаталары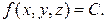 
теңдігін қанағаттандыратын 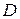анықталу облысының барлық 
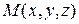нүктелер жиынын айтады.
5-мысал.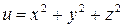 
функциясын қараймыз, 
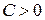болғанда деңгей беттері радиусы 
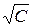-ға тең центрі координаталар басында болатын сфералар. 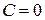болғанда деңгей беті координаталар басы болады. 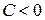бұл функцияның деңгей беттері жоқ.
Бірнеше айнымалы функцияның шегі мен үзіліссіздігі.
Жоғарыда көрсетілген екі – үш айнымалылы функциялардың ұғымдарын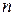 
айнымалы жағдайға жалғастырайық.. 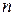айнымалының функциясы 
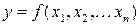деп, анықталу облысы 
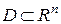- ге жататын, ал мәндер облысы нақты өсьте жататын функцияны атайды. Мұндай функциядағы әрбір 
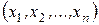айнымалылар тобы 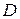-дан алынған, жалғыз 
санына сәйкес қояды. 
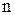санды айнымалысы бар функцияның ең жақсы берілу әдісі – аналитикалық әдіс.
Анықтама.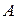 
саны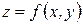 
функциясының 
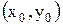нүктесіндегі шегі деп аталады, егер әрбір 
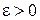үшін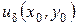 
аймағындағы барлық 
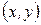үшін, осы нүктеден басқа, төмендегі теңсіздік 
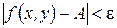орындалатындай 
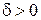саны табылса.. Егер 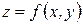функциясының 
нүктесіндегі шегі 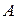болса, онда ол мына түрде белгіленеді: 
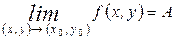. Бір айнымалы функциялар үшін қарастырылған барлық қасиеттер көп айнымалы функциялар үшін де дұрыс болады.
Анықтама. 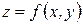функциясы нүктесінде үзіліссіз деп аталады, егер төменгі үш шарт орындалса:1)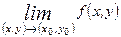 
бар болса,
2) нүктесінде функцияның мәні бар,
3) 
.
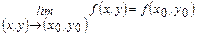Функцияның үзіліссіздігін келесі теореманың көмегімен зерттеуге болады.
Теорема. К ез келген 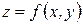элементар функция өзінің анықталу облысының барлық ішкі нүктелерінде (шеткі нүктелерінде емес) үзіліссіз болады.
6-мысал.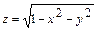 
Функциясының үзіліссіз болатын барлық нүктелерін табайық.. Бұрын айтқандай, бұл функция жабық 
дөңгелекте анықталған. Бұл дөнгелектің ішкі нүктелері функцияның ізделінді үзіліссіздік нүктелері, немесе 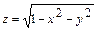функциясы ашық 
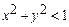дөнгелекте үзіліссіз.
Әдебиеттер: 9 нег.[232-241], 11 нег. [304-307].
Бақылау сұрақтар:
1. Екі айнымалы функцияның анықтамасын айту.
2. Бірнеше айнымалы функцияға мысал келтіру.
3. Екі айнымалы функцияның үзіліссіздігі.
4. Екі айнымалы функцияның шегі туралы ұғым.
5. Шектелген тұйық облыстағы функцияның кейбір қасиеттері туралы.
