Жиын ұғымы. Жиын туралы ұғым-математиканың ең негізгі ұғымы. Жиын деп әртүрлі заттардың жиынтығын атайды. Жиынның құрамындағы заттар оның элементтері деп аталады. Әдетте, жиынды латын алфавитінің үлкен 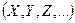 , ал оның сәйкес элементтерін – кіші
, ал оның сәйкес элементтерін – кіші  әріптерімен белгілейді. Жиынды құрайтын элементтерінің саны шектеулі де, шексіз көп болуы да мүмкін.
әріптерімен белгілейді. Жиынды құрайтын элементтерінің саны шектеулі де, шексіз көп болуы да мүмкін.  арқылы немесе
арқылы немесе  арқылы өрнектеледі. Бірде-бір элементі жоқ жиынды бос жиын деп атайды да, Æ символымен белгілейді. Егер Х жиынының барлық элементері У жиынында жатса, онда Х жиыны У жиынының жиыншасы (ішкі жиыны) немесе У жиыны Х жиынын қамтиды
арқылы өрнектеледі. Бірде-бір элементі жоқ жиынды бос жиын деп атайды да, Æ символымен белгілейді. Егер Х жиынының барлық элементері У жиынында жатса, онда Х жиыны У жиынының жиыншасы (ішкі жиыны) немесе У жиыны Х жиынын қамтиды  дейді, ал егер олар бірдей элементтерден тұрса, (яғни,
дейді, ал егер олар бірдей элементтерден тұрса, (яғни,  және
және 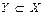 ), онда бұл жиындар тең
), онда бұл жиындар тең  дейді. Х пен У жиындарының ортақ элементтерінен тұратын
дейді. Х пен У жиындарының ортақ элементтерінен тұратын  жиынын олардың қиылысуы деп атайды да,
жиынын олардың қиылысуы деп атайды да,  символымен белгілейді. Х пен У жиындарының ең болмағанда біреуінде жататындай элементтерден тұратын
символымен белгілейді. Х пен У жиындарының ең болмағанда біреуінде жататындай элементтерден тұратын  жиынды олардың бірігуі деп атайды да,
жиынды олардың бірігуі деп атайды да, 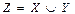 символымен белгілейді. Х, У жиындарының біреуінің екіншісінде жатпайтын элементтерінен тұратын
символымен белгілейді. Х, У жиындарының біреуінің екіншісінде жатпайтын элементтерінен тұратын  жиынды олардың айырымы деп атайды да,
жиынды олардың айырымы деп атайды да, 
 символымен белгілейді. У жиынына кірмейтін Х жиынының барлық элементтерінен тұратын
символымен белгілейді. У жиынына кірмейтін Х жиынының барлық элементтерінен тұратын  жиынды толықтауыш жиын деп атайды. Мысал.
жиынды толықтауыш жиын деп атайды. Мысал. 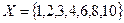 және
және  жиындары берілсін. Осы жиындардың бірігу, қиылысу, айырым және толықтауыш жиындарын табайық. Шешуі. Бірігуі-
жиындары берілсін. Осы жиындардың бірігу, қиылысу, айырым және толықтауыш жиындарын табайық. Шешуі. Бірігуі- 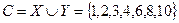 ; ал қиылысуы-
; ал қиылысуы- 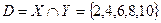 ; айырым жиыны-
; айырым жиыны-  ; ал толықтауыш жиыны -
; ал толықтауыш жиыны -  .
.
Сандар жиындары мынадай заңдылықтарға бағынады:  ;
;  . Барлық сандар жиындарының бірігу жиыны – нақты сандар жиыны, оны сандар өсі деп,
. Барлық сандар жиындарының бірігу жиыны – нақты сандар жиыны, оны сандар өсі деп,  символымен белгілейді.
символымен белгілейді.
Анықтама. Әртүрлі сандық мәндер қабылдайтын шамаларды айнымалы шамалар деп атайды.
Функция. Анықтама. Х жиынының кез келген х элементіне У жиынының кем дегенде бір у элементін сәйкес қоятын белгілі бір заңдылықты немесе ережені функция деп атайды да,  деп белгілейді. Мұндағы х -ті тәуелсіз айнымалы немесе аргумент деп, ал у айнымалысын тәуелді айнымалы немесе функция деп, х пен у -тің арасындағы байланыс функционалдық байланыс деп аталады. у -тің мәнін табу үшін х айнымалысына қолданылатын ереже
деп белгілейді. Мұндағы х -ті тәуелсіз айнымалы немесе аргумент деп, ал у айнымалысын тәуелді айнымалы немесе функция деп, х пен у -тің арасындағы байланыс функционалдық байланыс деп аталады. у -тің мәнін табу үшін х айнымалысына қолданылатын ереже 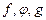 тағы басқа символдарымен белгіленеді. Мысалы,
тағы басқа символдарымен белгіленеді. Мысалы, 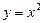 функциясындағы
функциясындағы  ережесі – квадраттау амалы. Функция мәндері өз мағынасын жоғалтпайтындай аргумент х -тің барлық нақты мәндер жиынын анықталу облысы дейді. Функцияның анықталу облысындағы қабылдайтын нақты мәндерінің жиынын оның өзгеру облысы деп атайды. Х, У жиындары нақты сандар болса, функция нақты сандық функция деп аталады.
ережесі – квадраттау амалы. Функция мәндері өз мағынасын жоғалтпайтындай аргумент х -тің барлық нақты мәндер жиынын анықталу облысы дейді. Функцияның анықталу облысындағы қабылдайтын нақты мәндерінің жиынын оның өзгеру облысы деп атайды. Х, У жиындары нақты сандар болса, функция нақты сандық функция деп аталады.
Мысалы, 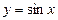 функциясының анықталу облысы
функциясының анықталу облысы  интервалы, ал өзгеру облысы
интервалы, ал өзгеру облысы  теңсіздігін қанағатандыратындай у -тің мәндері.
теңсіздігін қанағатандыратындай у -тің мәндері.
Функцияның берілу тәсілдері: аналитикалық, кестелік, графиктік. Абциссалары-тәуелсіз айнымалы, ал ординаталары-функция мәндері болып келген ХОУ жазықтығындағы  нүктелер жиынын
нүктелер жиынын  функциясының графигі дейді. Жалпы, функция бірмәнді де, көпмәнді де болып келуі мүмкін. Функцияның кейбір сипаттамаларына тоқталайық.
функциясының графигі дейді. Жалпы, функция бірмәнді де, көпмәнді де болып келуі мүмкін. Функцияның кейбір сипаттамаларына тоқталайық.
Егер барлық  үшін М саны бар болып
үшін М саны бар болып  теңсіздігі орындалса, онда
теңсіздігі орындалса, онда  функция өзінің Х -анықталу облысында шектелген деп аталады.
функция өзінің Х -анықталу облысында шектелген деп аталады.
Егер  функциясы Х жиынында жоғарыдан М (төменнен
функциясы Х жиынында жоғарыдан М (төменнен 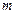 ) санымен шектелсе, онда осы
) санымен шектелсе, онда осы  санынан үлкен (кіші) барлық нақты сандар жиынының ең кіші (ең үлкен) элементін
санынан үлкен (кіші) барлық нақты сандар жиынының ең кіші (ең үлкен) элементін  функциясының сол жағындағы ең кіші жоғарғы - (ең үлкен төменгі) шекарасы немесе супремумы (инфимумы) деп атайды және оны
функциясының сол жағындағы ең кіші жоғарғы - (ең үлкен төменгі) шекарасы немесе супремумы (инфимумы) деп атайды және оны 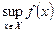
 символымен белгілейді.
символымен белгілейді.
Егер  функциясының анықталу облысындағы барлық
функциясының анықталу облысындағы барлық  үшін
үшін 
 теңдігі орындалса, онда ол жұп (тақ) функция деп аталады. Жұп функцияның графигі ОУ өсіне қатысты, тақ функция графигі бас нүктеге қатысты симметриялы болады.
теңдігі орындалса, онда ол жұп (тақ) функция деп аталады. Жұп функцияның графигі ОУ өсіне қатысты, тақ функция графигі бас нүктеге қатысты симметриялы болады.
Жұп та, тақ та емес функциялар да бар, ондай функцияларды жалпы түрдегі функциялар деп атайды. Мысалы,  ;
;  .
.
Егер  функциясының анықталу облысындағы барлық
функциясының анықталу облысындағы барлық  үшін
үшін  теңдігі орындалатындай тұрақты Т саны табылса, онда ол периодты функция деп аталады. Анықтамадағы теңдікті қанағаттандыратындай оң Т сандарының ең кішісін функцияның периоды дейді. Мысалы,
теңдігі орындалатындай тұрақты Т саны табылса, онда ол периодты функция деп аталады. Анықтамадағы теңдікті қанағаттандыратындай оң Т сандарының ең кішісін функцияның периоды дейді. Мысалы, 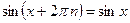 ,
,  ,
,  ;
;  -периоды
-периоды  болатын функциялар.
болатын функциялар.
Негізгі элементар функцияларға дәрежелік, көрсеткіштік, логарифмдік, тригонометриялық және кері тригонометриялық функциялар жатады. Негізгі элементар функцияларға арифметикалық төрт амал мен күрделі функция алуды шектеулі рет қолданудың нәтижесі болатын функцияны элементар функция деп атайды.
Тізбек шегі. Анықтама. Егер бір заңдылықпен, не ережемен әрбір  натурал санына сәйкес нақты бір ғана
натурал санына сәйкес нақты бір ғана 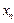 мәні анықталса, онда біз санды тізбек берілді дейміз. Санды тізбек
мәні анықталса, онда біз санды тізбек берілді дейміз. Санды тізбек  немесе
немесе  символдарымен белгіленеді;
символдарымен белгіленеді; 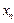 -оның жалпы мүшесі немесе
-оның жалпы мүшесі немесе  -ші мүшесі деп аталады.
-ші мүшесі деп аталады.  , сондықтан, тізбекті натурал аргументтің функциясы деп те атайды. Тізбектің геометриялық кескіні-абсцисса өсіндегі нүктелер. Санды тізбекке арифметикалық амалдар қолдана отырып, жаңа санды тізбек алуға болады.
, сондықтан, тізбекті натурал аргументтің функциясы деп те атайды. Тізбектің геометриялық кескіні-абсцисса өсіндегі нүктелер. Санды тізбекке арифметикалық амалдар қолдана отырып, жаңа санды тізбек алуға болады.
Анықтама. Егер М және 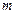 сандары бар болып,
сандары бар болып,  тізбегінің кез келген
тізбегінің кез келген 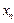 мүшесі үшін
мүшесі үшін 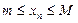 теңсіздігі орындалса, онда санды тізбек шектелген деп аталады. Егер тізбек ешбір санмен шектелмеген болса, онда оны шектеусіз тізбек деп атайды.
теңсіздігі орындалса, онда санды тізбек шектелген деп аталады. Егер тізбек ешбір санмен шектелмеген болса, онда оны шектеусіз тізбек деп атайды.
1. 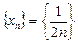 тізбегі шектелген, себебі, оның мүшелері үшін
тізбегі шектелген, себебі, оның мүшелері үшін  теңсіздігі орындалады.
теңсіздігі орындалады.
2.  тізбегі шектелмеген, себебі, А -ның қандай мәнінде болмасын тізбектің бір
тізбегі шектелмеген, себебі, А -ның қандай мәнінде болмасын тізбектің бір 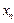 мәні табылып,
мәні табылып,  теңсіздігі орындалады.
теңсіздігі орындалады.
Анықтама. Егер кез келген  оң саны үшін
оң саны үшін  нөмірі табылып, барлық
нөмірі табылып, барлық  үшін
үшін  теңсіздігі орындалса, онда а саны
теңсіздігі орындалса, онда а саны  тізбегінің шегі деп аталады. Яғни,
тізбегінің шегі деп аталады. Яғни,  . Немесе,
. Немесе,  ,
,  символымен де белгілейді. Бұл жағдайда
символымен де белгілейді. Бұл жағдайда  тізбегін жинақты тізбек дейміз. Егер
тізбегін жинақты тізбек дейміз. Егер  тізбегінің шектелген шегі болмаса, онда ол жинақсыз тізбек деп аталады.
тізбегінің шектелген шегі болмаса, онда ол жинақсыз тізбек деп аталады.
Геометриялық мағынасы: егер а саны  тізбегінің шегі болса, онда белгілі бір нөмірден бастап тізбектің барлық мүшелері а нүктенің кез келген
тізбегінің шегі болса, онда белгілі бір нөмірден бастап тізбектің барлық мүшелері а нүктенің кез келген  аймағында жатады, яғни тізбектің шектелген санды мүшелері ғана
аймағында жатады, яғни тізбектің шектелген санды мүшелері ғана  аймағынан тысқары жатады.
аймағынан тысқары жатады.
Мысал.  тізбегі берілсін. Осы тізбектің шегі 1 болатынын, яғни кез келген
тізбегі берілсін. Осы тізбектің шегі 1 болатынын, яғни кез келген  саны үшін
саны үшін  теңсіздігі орындалатынын дәлелдейік.
теңсіздігі орындалатынын дәлелдейік.
Шешуі. Осы теңсіздіктің  нөмірінің қандай мәнінен бастап орындалатынын анықтау үшін оны шешу жеткілікті, яғни
нөмірінің қандай мәнінен бастап орындалатынын анықтау үшін оны шешу жеткілікті, яғни  немесе
немесе 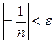 . Бұдан
. Бұдан  . Сонымен,
. Сонымен, 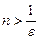 болғанда ғана
болғанда ғана  теңсіздігі орындалады. Демек,
теңсіздігі орындалады. Демек, 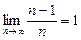 .
.
Жинақты тізбек туралы теоремалар.
1. Жинақты  тізбегінің тек бір ғана шегі бар. 2. Жинақты
тізбегінің тек бір ғана шегі бар. 2. Жинақты  тізбек шектелген.
тізбек шектелген.
3.  . 4.
. 4.  .
.
5. 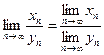 , мұндағы
, мұндағы  . 6.
. 6.  .
.
7.  .
.
Функцияның шегі.  оң санын алып,
оң санын алып,  болса, онда
болса, онда  . а нүктесі ішкі нүктесі болатын кез келген интервал а нүктесінің аймағы деп,
. а нүктесі ішкі нүктесі болатын кез келген интервал а нүктесінің аймағы деп,  интервалы а нүктесінің
интервалы а нүктесінің  -аймағы деп аталады.
-аймағы деп аталады.
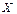 жиынында жатқан
жиынында жатқан  нүктенің кез келген
нүктенің кез келген  аймағы және осы аймақтың
аймағы және осы аймақтың  нүктеден өзге нүктелерінде анықталған
нүктеден өзге нүктелерінде анықталған  функциясы берілсін.
функциясы берілсін.
Функцияның нүктедегі шегінің анықтамасы. Егер  саны үшін
саны үшін  саны табылып, мына теңсіздікті
саны табылып, мына теңсіздікті 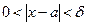 қанағаттандыратын барлық
қанағаттандыратын барлық  үшін
үшін  теңсіздігі орындалса, онда А саны х -тің а -ға ұмтылғандағы
теңсіздігі орындалса, онда А саны х -тің а -ға ұмтылғандағы  функциясының шегі деп аталады және оны
функциясының шегі деп аталады және оны  немесе
немесе  ,
,  символдарымен белгілейді. Функцияның
символдарымен белгілейді. Функцияның  нүктесіндегі шегі х -тің а -ға қалай ұмтылатындығына тәуелсіз болады. а -шектік нүкте. Геометриялық мағынасы:
нүктесіндегі шегі х -тің а -ға қалай ұмтылатындығына тәуелсіз болады. а -шектік нүкте. Геометриялық мағынасы: 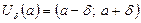 аймағындағы барлық нүктелерге сәйкес келетін
аймағындағы барлық нүктелерге сәйкес келетін  функциясының мәндері
функциясының мәндері  аймағында жатады. Яғни, барлық
аймағында жатады. Яғни, барлық  ,
,  үшін
үшін  функциясының графигі
функциясының графигі  параллель түзулердің аралығында жатады.
параллель түзулердің аралығында жатады.  (1-сурет).
(1-сурет).
Мысал.  дәлелдеу керек. Дәлелдемесі. Анықталу облысы:
дәлелдеу керек. Дәлелдемесі. Анықталу облысы:  .
. 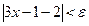 теңсіздігі орындалатындай әрбір
теңсіздігі орындалатындай әрбір  саны үшін
саны үшін  теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын  санының табылатынын көрсетейік:
санының табылатынын көрсетейік:
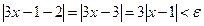 немесе
немесе  . Сондықтан,
. Сондықтан,  саны үшін
саны үшін  -санынан аспайтын санды алуға болады. Демек,
-санынан аспайтын санды алуға болады. Демек,  деп алсақ, онда
деп алсақ, онда  функциясының 2-ден айырмашылығы
функциясының 2-ден айырмашылығы  санынан кем болады. х айнымалысы
санынан кем болады. х айнымалысы  аймағына кірсе,
аймағына кірсе,  функциясының мәні де
функциясының мәні де  интервалына кіреді және одан ешқайда шыға алмайды, яғни
интервалына кіреді және одан ешқайда шыға алмайды, яғни  теңсіздігі орындалады.
теңсіздігі орындалады.
Теорема. Функцияның нүктедегі шегі бар болса, ол біреу ғана.
Функцияның шексіздіктегі шегінің анықтамасы. Егер кез келген  саны үшін
саны үшін  саны бар болып, барлық
саны бар болып, барлық 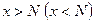 үшін
үшін  теңсіздігі орындалса, онда А саны х плюс (минус) шексіздікке ұмтылғандағы
теңсіздігі орындалса, онда А саны х плюс (минус) шексіздікке ұмтылғандағы  функциясының шегі деп аталады және ол
функциясының шегі деп аталады және ол  (
( ) символдарымен белгіленеді.
) символдарымен белгіленеді.
Осы анықтамадан,  болса, онда
болса, онда 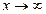 ұмтылғанда
ұмтылғанда  -тің мәні А санына ұмтылады, ал функция графигі
-тің мәні А санына ұмтылады, ал функция графигі  асимптотасына жуықтайды (2-сурет).
асимптотасына жуықтайды (2-сурет).
Тізбектің шегі туралы теоремалар функция шегі үшін де орындалады.
Теорема. Егер  ұмтылғанда (
ұмтылғанда ( -ақырлы сан немесе
-ақырлы сан немесе 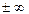 )
)  және
және  функцияларының ақырлы шектері бар болса, онда:
функцияларының ақырлы шектері бар болса, онда:
1)  2)
2) 
3) 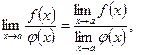 егер
егер  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
Элементар функциялар үшін олардың анықталу облысында мына теңдік орындалады:  .
.
Егер теореманың ең болмағанда бір шарты орындалмаса, онда  және т.б. түрдегі анықталмаған өрнектер пайда болады. Мұндай өрнектердің шегін табу анықталмағандықтарды шешу деп аталады. Ол үшін анықталмаған өрнектерді түрлендіру, тамаша шектер, Лопиталь ережелері қолданылады.
және т.б. түрдегі анықталмаған өрнектер пайда болады. Мұндай өрнектердің шегін табу анықталмағандықтарды шешу деп аталады. Ол үшін анықталмаған өрнектерді түрлендіру, тамаша шектер, Лопиталь ережелері қолданылады.
Тамаша шектер. 1.  2.
2.  .
. 


1-сурет 2-сурет
Бақылау сұрақтары:
1. Функцияның негізгі сипаттамалары қандай?
2. Тізбек дегеніміз не? Жинақты тізбек дегеніміз не?
3. Функцияның  ұмтылғандағы шегі бар болуы үшін оның
ұмтылғандағы шегі бар болуы үшін оның  нүктесіндегі мәні бар болуы керек пе?
нүктесіндегі мәні бар болуы керек пе?
4. Функцияның шегі туралы негізгі теоремалар қандай?
Негізгі әдебиет: [1], тарау, § 1.1-1.15 (3-77 беттер).
Қосымша әдебиет: [17], 3 тарау, § 3.1, 3.2, 3.4-3.9 (132-136, 138-154 беттер).






