Числовыми характеристиками сл.в. являются математическое ожидание M(X), дисперсия D(X), среднее квадратичное отклонение 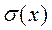 .
.
Опр. Математическим ожиданием дискретной сл.в. Х с законом распределения называется число
| Х | х1 | х2 | х3 | … | хn |
| Р | р1 | р2 | р3 | … | рn |
M(X)=x1p1+x2p2+…+xnpn
Пример. Найти М(Х) числа очков, выпадающих при бросании игральной кости.
Решение. Закон распределения имеет вид
| Х | ||||||
| Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Тогда М(Х)= 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6=3,5
Свойства М(Х):
1. М(СХ)=С*М(Х).
2. М(Х+У)=М(Х)+М(У)
3. М(Х*У)=М(Х)*М(У)
Опр. Пусть Х – дискретная сл.в., возможные значения которой х1,х2,…,хn,
М(Х) – математическое ожидание, тогда сл.в. Х-М(Х) называется отклонением величины Х от ее математического ожидания, т.е. отклонение это сл.в., которая принимает значения: х1-М(Х), х2-М(Х),…, хn-М(Х).
Опр. Дисперсией сл.в. называется математическое ожидание квадрата
отклонения сл.в. от ее математического ожидания.
Дисперсия обозначается 
Опр.. Средним квадратичным отклонением сл.в. Х называется корень
квадратный из дисперсии. 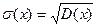 .
.
На практике часто используют формулу 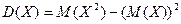 .
.
Пример. Дискретная сл.в. имеет закон распределения
| Х | |||
| Р | 0,3 | 0,5 | 0,2 |
Найти D(X)? 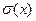 ?
?
Решение: М(Х)= 0*0,3+1*0,5+2*0,2=0,9
Запишем закон распределения отклонения этой величины, т.е. величины 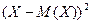
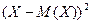
| (0-0,9) 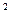
| (1-0,9) 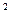
| (2-0,9) 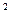
|
| Р | 0,3 | 0,5 | 0,2 |
D(X)=(0-0,9) 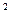 *0,3+(1-0,9)
*0,3+(1-0,9) 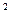 *0,5+(2-0,9)
*0,5+(2-0,9) 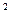 *0,2=0,81*0,3+0,01*0,5+1,21*0,2=0,49.
*0,2=0,81*0,3+0,01*0,5+1,21*0,2=0,49.
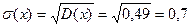
Контрольная работа по «Математике»
ВАРИАНТ 1
- Упростить алгебраическое выражение
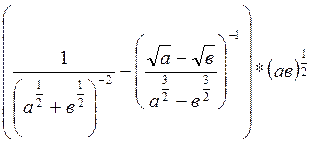
- Вычислить предел последовательности

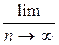


- Вычислить предел последовательности
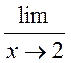

- Вычислить предел функции

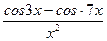
- Найти производную функции
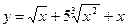
- Найти интервалы монотонности и точки экстремума функции
f(х)=  х
х 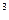 - 7.5 х
- 7.5 х 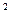 +18х
+18х
Найти неопределенный интеграл
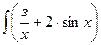 dx
dx
- Вычислить площадь фигуры, ограниченной линиями
у= х 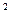 +х и у=х+1
+х и у=х+1
Найти частное решение дифференциального уравнения
(х+1) 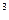 dу + (y-2)
dу + (y-2) 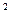 dx=0 при х
dx=0 при х  =1; y
=1; y  =4
=4
Исследовать на сходимость ряд, составленный из членов
Геометрической прогрессии
1+q+q 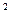 +…+ q
+…+ q 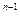 +…,
+…, 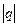 <1
<1
 ВАРИАНТ 2
ВАРИАНТ 2
Упростить алгебраическое выражение
а * 

Вычислить предел последовательности
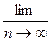

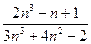
Вычислить предел последовательности
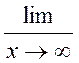


Вычислить предел функции
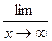

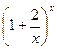
- Найти производную функции
у = 4е 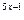
- Найти экстремумы функции
f(х)= (х – 2) 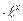
- Найти неопределенный интеграл
 dx
dx
Вычислить площадь фигуры, ограниченной линиями
у= -2х 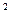 +3х+6 и у=х+2
+3х+6 и у=х+2
Найти частное решение дифференциального уравнения
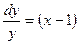 dx при х
dx при х  =2; y
=2; y  =5
=5
Исследовать на сходимость ряд
1+1+1+…+ 1+…
 ВАРИАНТ 3
ВАРИАНТ 3
Упростить алгебраическое выражение
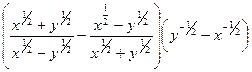

Вычислить предел последовательности
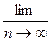

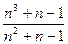
Вычислить предел последовательности


Вычислить предел функции

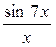
Найти производную функции
у = х 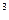 *sin х+
*sin х+ 
Найти наибольшее и наименьшее значение функции
f(х)= х 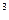 - 2х
- 2х 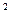 +х-2 на отрезке [0,5; 2]
+х-2 на отрезке [0,5; 2]
Найти неопределенный интеграл
 sin
sin 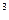 х dx
х dx
Вычислить площадь фигуры, ограниченной линиями
у = х 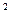 ; у =
; у = 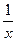 ; у = 0; х = 2
; у = 0; х = 2
Найти частное решение дифференциального уравнения
ху 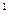 -у=0 при х
-у=0 при х  = -4; y
= -4; y  = 2
= 2
10. Исследовать ряд 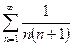 на сходимость
на сходимость
 ВАРИАНТ 4
ВАРИАНТ 4




