Представление физических величин квантовомеханическими операторами
В физике принимают как постулат идею о том, что каждой измеряемой физической величине А соответствует квантовомеханический оператор Â, такой, что действие этого оператора на собственную волновую функцию 
дает физически измеримую величину, умноженную на эту функцию
. (6.1)
Единственно возможным результатом измерений физической величины является собственное значение соответствующего оператора.
Полная энергия есть сумма кинетической и потенциальной. Тогда из (4.1) и (4.3) следует, что оператор полной энергии
− (операция дифференцирования по времени), (6.2)
оператор кинетической энергии
, - (операция дифференцирования по координатам), (6.3)
оператор потенциальной энергии
− (операция умножения). (6.4)
Для одномерной задачи
. (6.5)
Из связи между кинетической энергией и импульсом р
следует, что оператор импульса
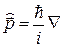, (6.6)
а его проекции на декартовы координатные оси
. (6.7)
Операторы координат
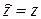− (операция умножения) (6.8)
Момент импульса частицы 
относительно начала координат в классической физике определяется векторным произведением радиус – вектора и импульса. В квантовой механике такое определение не имеет смысла, поскольку не существует состояния, в котором бы оба вектора 
и 
имели определенные значения. В квантовой механике векторному произведению 
соответствует оператор
, (6.9)
а его проекции на декартовы оси
(6.10)
Квантование момента импульса
При изучении движения в центрально симметричном поле важную роль играет момент импульса относительно неподвижного центра (для атома таким центром является ядро). Его значение связано с тем, что сохраняется, если система изолирована или движется в центральном силовом поле.
Для определения вектора момента импульса (его величины и направления) нужно знать все три его проекции. В квантовой механике существует теорема о том, что две величины А и В измеримы одновременно только, если соответствующие им операторы 
и 
коммутируют, т.е. удовлетворяют соотношению
.
Используя соотношения (6.10) нетрудно показать, что
Таким образом, любые две проекции оператора момента импульса не коммутируют между собой. Поэтому не существует состояния, в котором бы все три проекции и даже какие – либо две из трех проекций имели определенные значения. Значит, не существует состояния, в котором бы сам вектор момента импульса имел определенное значение, т.е. был бы полностью определен как по величине, так и по направлению. Иными словами, оператор момента импульса 
не имеет собственных функций и соответствующих им собственных значений.
Можно показать, что коммутирующими операторами являются оператор квадрата момента импульса и оператор проекции момента импульса на некоторое направление. Следовательно, характеристиками данного состояния являются модуль момента импульса и его проекция на некоторое выделенное направление, которые можно одновременно определить.
Перейдя от декартовых координат к сферическим, получим
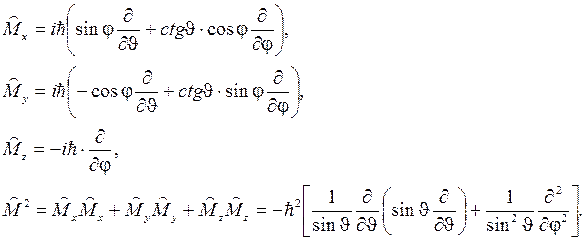(6.11)
Вычислим проекцию момента импульса на ось z, приняв во внимание (5.14)
(6.12)
Теперь найдем квадрат модуля момента импульса. Используя выражения (6.11), (5.10) и (5.11), запишем
Из (5.12) следует, что выражение в квадратных скобках равно 
. Тогда
, 
. (6.13)
Таким образом, орбитальное или азимутальное квантовое число l определяет разрешенные значения момента импульса частицы, а магнитное квантовое число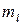 
− значения его проекции на выделенное направление. Напомним, что разрешенные значения энергии атома задаются квантовым числом п, которое называется главным квантовым числом.
Отметим еще раз, что классический и квантовый моменты импульса существенно различаются.
Во-первых, классический момент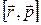 
зависит от выбора точки О, относительно которой берется радиус–вектор. В квантовой теории момент импульса не зависит от выбора точки О.
Во-вторых, модуль момента импульса может быть задан точно, но при этом его направление не определено. Вместе с заданием модуля момента импульса можно задать его проекцию лишь на одну из координатных осей, например, z, две другие проекции могут быть любыми. Целочисленность (в единицах 
) проекции момента импульса можно истолковать как квантование ориентации вектора (правда, только относительно одной оси). Пространственная ориентация его остается неизвестной.
Проекция вектора не может быть больше его модуля (
). Поэтому должно выполняться условие 
, т.е. максимальное значение 
равно l. Отсюда следует, что число 
принимает значения
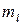= 0, ±1, ±2, …± l, (6.14)
и всего при заданном l число 
может иметь значений 
.
Таким образом, в квантовой теории можно определить модуль момента импульса и его проекцию на одну координатную ось (ось произвольна). Направление же этого вектора остается неопределенным.
Для наглядности пространственное квантование момента импульса обычно представляют графически на векторных диаграммах. По оси z откладывают возможные значения 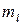, рассматривая их как проекции вектора длины 
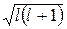, имеющего дискретные направления в пространстве. Неопределенность остальных двух проекций представляют как прецессию этого вектора относительно оси z. В качестве примера на рис.6.1 приведена векторная диаграмма для случая l = 2 (за единицу момента принята постоянная Планка ). Эту диаграмму нельзя понимать буквально. Она правильно передает Рис. 6.1 только два факта: возможные значения 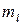и l.
Магнитный момент атома водорода
Пусть по классическим представлениям электрон движется со скоростью V по орбите радиусом r. Через площадку, пересекающую его орбиту, переносится ежесекундно заряд 
(е – заряд электрона, 
число оборотов электрона вокруг ядра в секунду) Скорость электрона можно представить 
. Движущийся по орбите электрон образует круговой ток. Магнитный момент такого тока в системе СИ равен 
. Учитывая, что момент импульса электрона 
, получим
. (6.15)
Знак минус указывает, что направления обоих моментов противоположны, поскольку для отрицательно заряженного электрона направление тока противоположно направлению его движения. Соотношение (6.15) называют гиромагнитным отношением. Оно справедливо и в квантовой теории.
Тогда, принимая во внимание (6.15) и (6.13), можно записать
, (6.16)
. (6.17)
Постоянная величина 
называется магнетоном Бора. Ее значение в системе СИ 
. (В гауссовой системе единиц 
)
Лекция 7
