Аналогично случаю прямых на плоскости, можно доказать, что две плоскости, заданные своими общими уравнениями  и
и 
· совпадают при 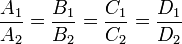
· параллельны при 
· пересекаются в остальных случаях.
Полупространства, связанные с данным уравнением плоскости
Пусть дана плоскость в пространстве. Две точки  и
и  лежат по одну сторону от плоскости, если отрезок
лежат по одну сторону от плоскости, если отрезок  не пересекается с данной плоскостью. Полупространством называют множество всех точек, которые лежат по одну сторону от плоскости.
не пересекается с данной плоскостью. Полупространством называют множество всех точек, которые лежат по одну сторону от плоскости.
Аналогично случаю прямой на плоскости множества  и
и  всех точек
всех точек  , для которых
, для которых  и
и 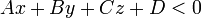 , являются полупространсвами, ограниченными плоскостью.
, являются полупространсвами, ограниченными плоскостью.
Множество  называют отрицательным полупространством по отношению к уравнению (14) плоскости, а
называют отрицательным полупространством по отношению к уравнению (14) плоскости, а  — положительным полупространством.
— положительным полупространством.
Цилиндрические координаты (рис. 4.6)
Главные значения  ,
,  ,
,  :
: 
Связь между декартовыми прямоугольными и цилиндрическими координатами:

Сферические координаты (рис. 4.7)
Главные значения  ,
,  ,
,  :
: 
Иногда вместо  рассматривают
рассматривают 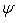 :
: 

Связь между декартовыми прямоугольными и сферическими координатами
 или
или 
Прямая на плоскости
Общее уравнение Ax + By + C ( > 0).
> 0).
Вектор 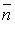 = (А; В) - нормальный вектор прямой.
= (А; В) - нормальный вектор прямой.
В векторном виде:  + С = 0, где
+ С = 0, где  - радиус-вектор произвольной точки на прямой (рис. 4.11).
- радиус-вектор произвольной точки на прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 - прямая параллельна оси Ox;
2) Ax + C = 0 - прямая параллельна оси Oy;
3) Ax + By = 0 - прямая проходит через начало координат;
4) y = 0 - ось Ox;
5) x = 0 - ось Oy.



Уравнение прямой в отрезках 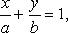 где a, b - величины отрезков, отсекаемых прямой на осях координат.
где a, b - величины отрезков, отсекаемых прямой на осях координат.
Нормальное уравнение прямой (рис. 4.11)

где  - угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.
- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.
Приведение общего уравнения прямой к нормальному виду:
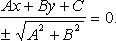
Здесь  - нормируемый множитель прямой; знак выбирается противоположным знаку C, если
- нормируемый множитель прямой; знак выбирается противоположным знаку C, если  и произвольно, если C = 0.
и произвольно, если C = 0.
Векторно-параметрическое уравнение прямой

где  - фиксированная точка, лежащая на прямой;
- фиксированная точка, лежащая на прямой;  - направляющий вектор (см. рис. 4.11).
- направляющий вектор (см. рис. 4.11).
В координатах (параметрические уравнения):


Каноническое уравнение прямой

Уравнение прямой по двум точкам (рис. 4.12)
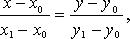
или

или

Уравнение прямой по точке и угловому коэффициенту (рис. 4.12)
 или
или 
где  b - величина отрезка, отсекаемого прямой на оси Oy.
b - величина отрезка, отсекаемого прямой на оси Oy.

Отклонение точки от прямой
 или
или 
где знак перед корнем противоположен знаку C, если  и выбран произвольно, если C = 0.
и выбран произвольно, если C = 0.
Расстояние от точки до прямой

Взаимное расположение двух прямых
Прямые  и
и  :
:
пересекаются 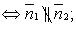
параллельны (но не совпадают) 
совпадают 
Прямые 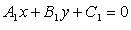 и
и  :
:
пересекаются 
параллельны (но не совпадают) 
совпадают 
Прямые  и
и  :
:
пересекаются 
параллельны (но не совпадают) 
совпадают 
Угол между двумя прямыми


Необходимое и достаточное условие перпендикулярности двух прямых
 или
или  или
или 
Расстояние между параллельными прямыми
Если прямые заданы уравнениями  и
и  то
то

а если уравнениями  и
и  то
то

Пучок прямых
Если  - центр пучка, то уравнение пучка
- центр пучка, то уравнение пучка

Если центр задан пересечением двух прямых
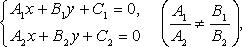
то уравнение пучка

Векторно-параметрическое уравнение прямой

где  - фиксированная точка, лежащая на прямой;
- фиксированная точка, лежащая на прямой;  - направляющий вектор.
- направляющий вектор.
В координатах (параметрические уравнения):



Канонические уравнения прямой

Уравнения прямой по двум точкам

Прямая как линия пересечения двух плоскостей

при условии, что не имеют места равенства
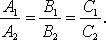
Направляющий вектор такой прямой

где







