Матрица, обратная к матрице 
обозначается 
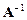. Если обратная матрица существует, то она единственна и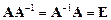 
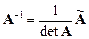, где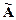 
– присоединенная (союзная), составленная из алгебраических дополнений 
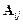j: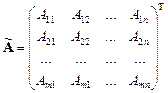 
Тогда определитель обратной матрицы связан с определителем данной матрицы следующим соотношением: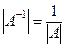 
. В самом деле, 
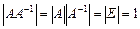, откуда и следует данное равенство.
Свойства обратной матрицы:
1. 
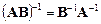, где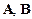 
‑ невырожденные квадратные матрицы одинакового порядка.
2. 
.
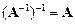3. 
.
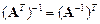4. 
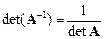
Лекция 1.3. Решение систем линейных уравнений методом Крамера.методам Гаусса и средствами матричного исчисления.
Краткое содержание: Метод Крамера и метод Гаусса решения систем линейных алгебраических уравнений. Матричный способ решения систем уравнений. Ранг матрицы. Теорема Кронекера-Капелли. Фундаментальная система решений. Однородные и неоднородные системы.
Система уравнений следующего вида:
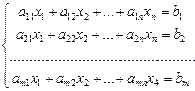(*), где 
, 
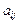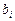‑ коэффициенты, 
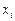‑ переменные, называется системой линейных уравнений. Решить систему линейных уравнений – это значит указать все решения системы, т.е. такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется:
а) совместной, если она имеет хотя бы одно решение;
б) несовместной, если она не имеет решений;
в) определенной, если она имеет единственное решение;
г) однородной, если все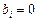 
;
д) неоднородной, если есть 
.
Систему линейных уравнений (*) можно записать короче: Ax=b, где A – матрица, составленная из коэффициентов 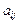, x – вектор столбец неизвестных 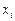, b – вектор столбец свободных членов .
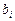Можно обозначить вектор переменных через x, вектор правых частей уравненийчерез b, а матрицу коэффициентов через A:
, 
, 
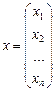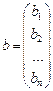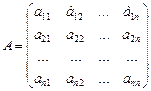
Тогда по определению матричного произведения систему линейных уравнений можно записать короче: Ax=b.
При исследовании системы линейных уравнений главную роль играет определитель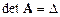 
составленный из коэффициентов системы. Его называют главным определителем системы. Введем еще n определителей: определитель 
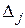получается из определителя 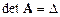заменой j–го столбца на столбец b правых частей уравнений (
).
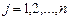Правило Крамера применяется к системам, у которых число уравнений m равно числу переменных n, т.е. m=n.
Правило Крамера:
1.Если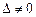 
, система Ax=b имеет единственное решение: 
, …, 
.
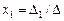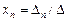2.Если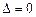 
, а хотя бы один из определителей 
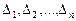не равен 0, система несовместна.
3.Если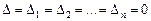 
, система имеет бесконечно много решений.
Метод Гаусса:
В случае систем большого числа уравнений удобно пользоваться методом Гаусса, который заключается в последовательном исключении неизвестных с помощью элементарных преобразований над строками и перестановкой столбцов. Процесс решения по методу Гаусса состоит из 2х этапов: на первом этапе система приводится к ступенчатому виду (прямой ход), на втором этапе идет последовательное нахождение неизвестных из этой системы (обратный ход) Рассмотрим метод на примере системы четырех уравнений с четырьмя неизвестными:
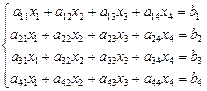
Допустим, что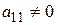 
(если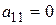 
, то изменим порядок уравнений, выбрав первым такое уравнение, в котором коэффициент при x не равен нулю).
Первый шаг: Делим первое уравнение на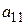 
, умножаем полученное уравнение на 
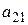и вычитаем из второго; затем умножаем на 
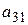и вычитаем из третьего; наконец умножаем на 
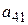и вычитаем из четвертого. В результате первого шага приходим к системе
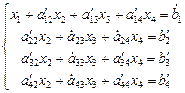
Второй шаг: Поступаем с вторым, третьим и четвертым уравнениями новой системы так же как на первом шаге. В итоге исходная система преобразуется к так называемому ступенчатому виду:
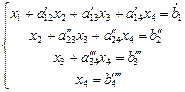
Из преобразованной системы все неизвестные определяются последовательно без труда.
Ранг Матрицы.
Рассмотрим матрицу А: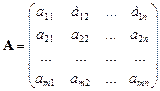 
Выделим в матрице k строк и k столбцов (k<=min(m,n)). Из элементов, стоящих на пересечении выделенных строк и столбцов составим определитель k-го порядка. Такие определители называются минорами k-го порядка этой матрицы. В нашей матрице выделен минор 2-го порядка.
Наибольший порядок миноров данной матрицы отличных от нуля наз. рангом матрицы
Обозначается r(A), rang(A),r. Очевидно, что r< min(m,n). Минор, порядок которого определяет ранг матрицы наз. базисным.
Свойства ранга матрицы:
1. При транспонировании матрицы ее ранг не меняется
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится
3. Ранг матрицы не меняется при элементарных преобразованиях
Системы 2-х и 3-х линейных уравнений.
Пусть мы умеем вычислять определители (n-1)-го порядка и задана квадратная матрица n-го порядка
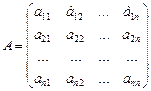. Тогда определителем матрицы А (определителем n-го порядка) называется число, не зависящее от номера строки по которой разлагается определитель: 
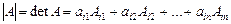. Аналогично определитель n-го порядка можно разложить и по j–му столбцу: 
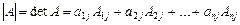. Где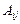 
алгебраическое дополнение элемента .
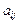С помощью определителей n-го порядка можно исследовать системы линейных уравнений с n неизвестными.
Рассмотрим систему линейных уравнений n-го порядка:
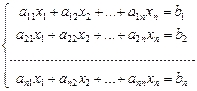
Т1. Кронекера-Капелли
Система линейных алгебраических уравнений совместна т.и.т.т., если ранг ее основной матрицы равен рангу расширенной
Т2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение
Т3. Если ранг совместной системы меньше числа неизвестных, то система имеет множество решений
( Если система имеет хотя бы одно решение, она называется совместной. Если она не имеет ни одного решения, то несовместной.
Совместная система наз. определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Система наз. однородной, если все свободные члены равны 0)
Правило решения произвольной системы уравнений:
1.Найти ранг основной и расширенной матриц, если они одинаковы – система совместна и имеет решение.
2.Если система совместна, то выбрать какой-либо базисный минор, взять r уравнений (остальные отбросить). Неизвестные коэффициенты, которые входят в базисный минор называются главными, остальные свободными, их переносят в правые части
3.Найти выражения главных через свободные.
Придавая свободным переменным
Матричный способ решения систем алгебраических уравнений:
Пусть задана система алгебраических уравнений, которая записана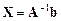 
. Если 
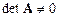, то существует обратная матрица 
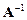. Умножим слева на 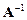наше матричное уравнение: 
, 
,
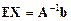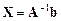
Нахождение обратной матрицы методом Гаусса:
Припишем к матрице А единичную матрицу Е такого же порядка, что и А: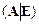 
. Преобразованиями из метода Гаусса получим на месте А единичную матрицу Е. Тогда на месте Е будет : 
.
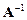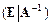