Лекция 2.1. Векторы. Линейные операции над векторами.
Краткое содержание: Векторы. Линейные операции над векторами и их свойства. Декартовы координаты вектора и точки. Линейные операции над векторами в координатах.
Прямоугольные декартовы координаты на плоскости это выбранная на плоскости точка О (начало координат) и проходящие через нее взаимно перпендикулярные направленные прямые Ox и Oy (оси координат).
В пространстве это три взаимно перпендикулярные оси (оси координат), исходящие из общей точки О (начало координат) и образующие правую тройку (правая система кординат). Иными словами для наблюдателя, направленного по оси Oz кратчайший поворот оси Ox к оси Oy происходит против хода часовой стрелки. Три взаимно перпендикулярные плоскости Oyz, Ozx, Oxy проходящие через соответствующие оси, называются координатными плоскостями.
Величина, кроме числового значения характеризуемая еще и направлением называется вектором. При этом используется обозначение 
, где точка А – начало отрезка, а точка В – его конец. Если начало и конец вектора совпадают, вектор называется нулевым и обозначается 
.
Расстояние между началом и концом вектора называется его длиной: 
. Длина нулевого вектора равна нулю 
.
Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной и той же прямой. Коллинеарность обозначается как параллельность: 
. Коллинеарные векторы могут быть направлены одинаково или противоположно.
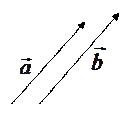
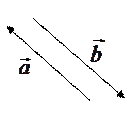
Два вектора называются равными (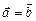
), если они коллинеарны, одинаково направлены и их длины равны.
Свободным называется вектор, который можно перемещать по плоскости параллельно самому себе, при этом получая вектор, равный данному.
Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Сложение векторов:
a) cуммой 
векторов 
и 
по правилу треугольника называется вектор, который идет из начальной точки вектора к конечной точке вектора , если приложен к конечной точке .
b) cуммой векторов и по правилу параллелограмма называется вектор-диагональ параллелограмма, выходящий из общей точки векторов и , если векторы отложены из одной точки и достроены до параллелограмма.
 | |||
 | |||
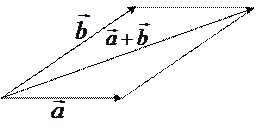Сложение векторов коммутативно, т.е.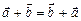 
.
Сложение векторов ассоциативно, т.е.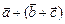 
= 
.
Суммой нескольких векторов называется вектор по величине и направлению равный замыкающей пространственной ломаной линии, построенной на данных векторах.
Для любого вектора : 
.
Для любого вектора справедливо: 
, вектор 
называют противоположным вектору и обозначают ‑ .
Под разностью векторов и понимается вектор 
, такой, что 
.
Произведением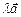 
вектора на число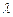 
называется вектор
а)коллинеарный ;
б)имеющий длину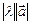 
;
в)имеющий направление при 
и противоположное направление при 
.
Свойства умножения вектора на число:
1) ненулевые векторы и коллинеарны тогда и только тогда, когда существует число 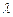, такое, что 
;
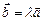2) умножение вектора на число ассоциативно относительно умножения чисел 
;
3) умножение вектора на число дистрибутивно относительно сложения чисел 
;
4)умножение вектора на число дистрибутивно относительно сложения векторов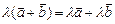 
;
5) 
, 
.
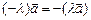Всякий вектор х может быть единственным образом представлен в виде: 
, где 
, 
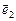пара ненулевых неколлинеарных векторов, которые образуют базис. Равенство называется разложением вектора х по данному базису, а числа 
, 
- координатами вектора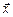 
при разложении по базису: 
.
С базисом на плоскости можно связать систему координат. О – начало координат. Каждой точке А на плоскости соответствует вектор 
- радиус вектор этой точки. Координаты радиуса-вектора при разложении по базису , 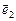называются координатами точки в построенной системе координат: 
Свойства:
1) если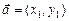 
, 
, то 
;
2) если 
, то 
;
3) вектор 
соединяющий точки 
и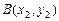 
имеет координаты 
;
4) векторы 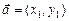, коллинеарны тогда и только тогда, когда их координаты пропорциональны: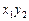 
= 
(
);
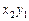5) длина (модуль) вектора вычисляется по формуле 
.
Три вектора 
, 
, 
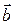называются компланарными, если они лежат в одной плоскости.
Тройка некомпланарных векторов , , 
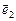в пространстве образуют базис. Равенство 
называется разложением вектора х по данному базису, а числа , , 
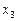- координатами вектора х при разложении по базису: 
.
Базис в пространстве порождает систему координат. Если отложить базисные векторы от начала координат, то за координаты точки принимаются координаты ее радиуса-вектора (вектора, идущего в данную точку из начала координат.
Свойства координат в пространстве:
1) если 
, 
, то 
;
2) если 
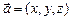, то 
;
3) вектор соединяющий точки 
и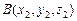 
имеет координаты 
;
4) векторы 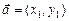, коллинеарны тогда и только тогда, когда их координаты пропорциональны: = ,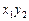 
= 
, 
= 
(
).
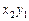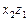5) длина (модуль) вектора 
вычисляется по формуле 
.
Самая распространенная система координат - декартова образуется двумя взаимно перпендикулярными векторами , , 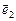длина которых равна 1. 
, 
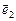; или тремя взаимно перпендикулярными векторами , , длина которых равна единице. 
, 
;.
В векторной форме условие коллинеарности можно записать так: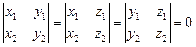 
А условие компланарности: 
Проекцией точки на прямую называется основание перпендикуляра, опущенного из точки на эту прямую. Проекцией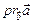 
вектора на вектор (или на направление ) называется вектор, началом которого служит проекция начала , а концом – проекция конца на прямую, содержащую .
Проекция вектора на ось равна произведению длины вектора на косинус угла между направлением вектора и направлением оси: 
, 
.
Свойства проекций:
1) равные векторы имеют равные проекции;
2) проекция суммы векторов равна сумме их проекций: 
;
3)проекция вектора на ось положительна, если вектор образует с осью острый угол, отрицательна, если угол тупой, равна нулю, если угол прямой;
4)проекция замкнутой векторной линии на любую ось равна нулю;
5)при умножении вектора на скаляр, его проекция на данную ось умножается на этот скаляр: 
.
Направление вектора определяется углами 
, 
, 
, образованными вектором с положительными направлениями осей 
, 
, 
соответственно. Косинусы этих углов называются направляющими косинусами вектора и определяются по следующим формулам:
, 
, 
Лекция 2.2. Скалярное, векторное и смешанное произведение векторов.
Краткое содержание: Скалярное произведение векторов, его свойства, координатное выражение. Векторное произведение векторов, его свойства, координатное выражение. Геометрические приложения скалярного и векторного произведения. Смешанное произведение векторов, его свойства, координатное выражение и геометрические приложения.
Введем еще одну операцию над векторами. Углом между ненулевыми векторами и называется угол между соответствующими лучами, если оба вектора приложить к одной точке Угол между векторами обозначают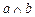 
.
Скалярным произведением векторов и , обозначаемым 
, называется число, равное произведению их длин и косинуса угла между ними: 
, где 
.
Свойства скалярного произведения векторов:
1) скалярное произведение коммутативно: 
;
2) для любого числа 
и любых векторов и справедливо равенство 
;
3) скалярный квадрат равен квадрату длины вектора: 
;
4) если 
, то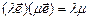 
;
5) 
тогда и только тогда, когда векторы и перпендикулярны (ортогональны) или один из них равен нулю;
6) 
;
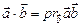7) скалярное произведение дистрибутивно относительно сложения векторов: 
Зная координаты векторов 
и 
в декартовой прямоугольной системе координат, для вычисления скалярного произведения векторов и можно воспользоваться следующей формулой: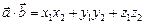 
.
Из равенства можно определить значение косинуса угла между векторами и : 
Векторное произведение.
Упорядоченная тройка некомпланарных векторов , , 
называется правой тройкой, если наблюдателю, находящемуся в конечной точке вектора , поворот от вектора к вектору на кратчайший угол виден совершающимся против часовой стрелки.
Если поворот от вектора к вектору на кратчайший угол виден совершающимся по часовой стрелке, то векторы , , образуют левую тройку.
 |
правая тройка левая тройка
Векторным произведением двух векторов и , обозначаемым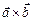 
, называется вектор, удовлетворяющий следующим условиям:
1) длина (модуль) векторного произведения равна 
, где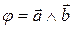 
. Т.е. модуль векторного произведения равен площади параллелограмма, построенного на этих векторах;
2) вектор 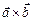перпендикулярен плоскости векторов и : ,
3) векторы , , образуют правую тройку.
Из определения ясно, что 
, если один из них нулевой или они коллинеарны (
).
Справедливы следующие свойства векторного произведения:
1) 
;
2) векторное произведение антикоммутативно: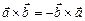 
;
3) 
, где 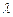‑ число (скаляр);
4) векторное произведение дистрибутивно относительно сложения векторов: 
.
Зная координаты векторов и в декартовой прямоугольной системе координат, для вычисления векторного произведения векторов и можно воспользоваться следующей формулой:
(определитель разложен по первой строке).
Смешанным произведением векторов , , называется число 
, которое равно скалярному произведению векторного произведения 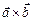и вектора : 
.
 |
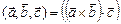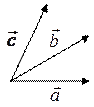Основные свойства смешанного произведения векторов:
1) 
, т.е. порядок двух операций (скалярное и векторное произведение векторов), дающих смешанное произведение векторов, не является существенным. Это свойство и позволяет обозначать смешанное произведение просто ;
2) 
, т.е. при нарушении цикличности перестановки векторов знак векторного произведения меняется на противоположный;
3) 
, где 
и 
- числа (скаляры).
Зная координаты векторов , и 
в декартовой прямоугольной системе координат, для вычисления смешанного произведения векторов , и можно воспользоваться следующей формулой:
= 
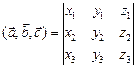Условие компланарности векторов: Смешанное произведение равно нулю тогда и только тогда, когда векторы , , компланарны.
В самом.деле, равенство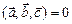 
означает, что векторы 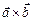и перпендикулярны. Но 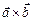есть вектор, перпендикулярный и и . Стало быть, 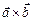перпендикулярен всем трем векторам одновременно. Это возможно лишь в случае, когда они лежат в одной плоскости;
Геометрический смысл смешанного произведения:
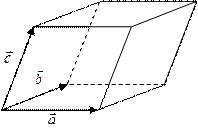Смешанное произведение равно объему параллелепипеда, построенного на векторах , , и взятого со знаком «+», если тройка правая, и со знаком «—», если тройка левая: 
.
Воспользовавшись геометрическим смыслом смешанного произведения векторов, можно определить тип тройки векторов по знаку смешанного произведения векторов. Если 
, то , , ‑ правая тройка векторов, если 
, то , , ‑ левая тройка векторов.
Полярная система координат.
| Говорят, что на плоскости введена полярная система координат, если заданы: 1) т.О (полюс); 2) полупрямая ОА (полярная ось); 3) масштаб для измерения длин. |
Положение произвольной точки М на плоскости определяется полярными координатами: полярным радиусом 
(
и полярным углом 
между полупрямыми 
и 
. Считают, что 
при повороте от к против часовой стрелки и 
при повороте от к по часовой стрелке. Полярный угол определен не однозначно – значение полярного угла, удовлетворяющее условию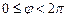 
, называется главным.
Определим связь между декартовыми координатами на плоскости и полярными координатами. Для этого совместим начало координат и полюс, а полярную ось направим по положительной полуоси абсцисс. Тогда декартовы координаты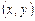 
и полярные координаты 
произвольной точки М связаны следующими соотношениями:
 и  .
|
При нахождении полярного угла необходимо учитывать, в какой координатной четверти расположена т. М и подобрать соответствующее значение .
