Отношение эквивалентности (оно рефлексивно, симметрично и транзитивно). То же, что и равносильность.
Логическое следствие
Высказывание 
является логическим следствием высказывания 
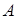, если формула 
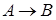является тождественно истинной. Высказывание является логическим следствием высказываний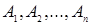 
, если 
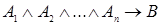− тождественно истинная формула.
Множество истинностных значений
Множество {И, Л}.
Молекула
Сложное высказывание, которое можно построить из атомов с использованием логических связок.
То же, что и формула в логике высказываний.
Невыполнимая формула
Формула, которая принимает значение «ложь» на всех интерпретациях.
То же, что и тождественно ложная формула или противоречивая формула.
Независимая система аксиом
Если ни одну из аксиом системы исчисления высказываний нельзя вывести из остальных, применяя правила вывода данной системы, то говорят, что система аксиом независима.
Необщезначимая формула
Формула, которая на одних интерпретациях принимает значение «истина», а на других – «ложь».
То же, что и непротиворечивая формула.
Непротиворечивая формула
То же, что и необщезначимая формула.
Непротиворечивое логическое исчисление
Логическое исчисление непротиворечиво, если в нем не выводимы никакие две формулы, из которых одна является отрицанием другой.
Нульместный предикат
Нульместным предикатом считается высказывание.
Область действия квантора
Формула 
в выражениях 
и 
, на которую распространяется действие квантора.
Область значений предиката
Фиксированное множество {И, Л}.
Область определения предиката
Множество значений 
, которое может принимать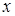 
в предикате .
То же, что универс или предметная область.
Общезначимая формула
Формула, которая принимает значение «истина» на всех интерпретациях (наборах значений переменных).
То же, что и тождественно истинная формула или тавтология.
Одноместный предикат
Предикат с одной переменной (может обозначаться, например, , где 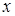− переменная).
Отрицание высказывания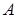 
Высказывание (обозначение 
), которое истинно тогда и только тогда, когда 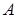ложно.
Порядок предиката
Количество аргументов предиката 
.
Посылка
В импликации 
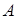высказывание называется посылкой.
То же, что и условие, антецедент.
Правило введения квантора всеобщности
утверждает истинность 
, если доказана истинность 
для любого 
, то есть для всех элементов из рассматриваемой предметной области 
.
