Рассмотрим влияние воздушного зазора на параметры катушки. Для упрощения будем считать, что катушка не имеет активного сопротивления и потоков рассеяния.
Сначала проанализируем влияние воздушного зазора 
на вид зависимости 
.
Второй закон Кирхгофа для магнитной цепи:
,
, 
- магнитные сопротивления
Рис.42. Катушка с воздушным зазором сердечника и зазора.
Магнитные сопротивления соответственно равны:
; 
.
Первая составляющая представляет собой вебер-амперную характеристику катушки без воздушного зазора (
=0). Из-за насыщения сердечника эта характеристика нелинейная (
- зависит от величины магнитной индукции). Вторая составляющая зависит от величины зазора и представляет собой прямую линию (
- постоянная). Сложив две составляющие, можно получить результирующую вебер-амперную характеристику катушки с зазором, представленную на рис.43.
Из приведенных зависимости видно, что воздушный зазор спрямляет ВАХ, делая ее более линейной на значительном участке. Также видно, что при заданном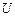 
с увеличением зазора намагничивающий ток катушки увеличивается, а полное сопротивление катушки 
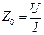уменьшается.
Рис.43. ВАХ катушки с воздушным зазором
Поэтому в тех случаях, когда величина зазора не задана техническими условиями аппарата, воздушный зазор с целью уменьшения намагничивающегося тока стремятся сделать как можно меньше.
Феррорезонанс напряжений
В электрических цепях, содержащих катушки с сердечниками и конденсаторы, наблюдаются особые явления, связанные с нелинейными свойствами катушек.
Рис.44. Цепь с феррорезонансом напряжений
а) схема цепи; б) векторная диаграмма
Рассмотрим явление, возникающие в цепи, состоящей из последовательного соединения катушки и конденсатора (рис.44.а).
Предположим, что в катушке отсутствуют потери энергии. В этом случае, напряжение на катушки 
опережает ток на 90о, 
отстает от тока также на 90о. Векторная диаграмма для такой цепи представлена на рис.44.б, из которой можно записать:
. (62)
Представим на рис.45.а зависимости 
и 
. Первая зависимость нелинейная и определяется видом кривой намагничивания. Результирующая зависимость 
является также нелинейной (см.рис.45.а).
Рис.45. Феррорезонанс напряжений
а) для идеализированной цепи; б) с учетом потерь
Согласно полученной характеристике при заданном значение напряжения 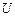возможно три установившихся режима цепи с токами 
, 
, 
. Если приложенное напряжение больше 
, то возможен только один определенный режим, при этом общий характер цепи емкостный.
Особая точка «а» является точкой резонанса, в этой точке 
= 
. В отличие от цепей с постоянными параметрами, резонанс в рассматриваемой цепи можно достичь изменением напряжения, так как индуктивность катушки зависит от протекающего тока. Это явление получило название феррорезонанса напряжения.
Область «ас» характеристики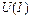 
является областью неустойчивых режимов. Действительно пусть установившийся режим характеризуется точкой «d». Тогда всякое случайное повышение тока приведет к уменьшению падения напряжения в цепи и к дальнейшему увеличению тока. Всякое случайное уменьшение тока, переводит состояние цепи из режима «d» в режим «e». Вследствие наличия в цепи потерь и высших гармоник, фактическая характеристика 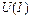цепи приобретает вид, указанный на рис.45.б. Опытным путем при изменении напряжения 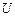, можно снять только часть характеристики. Участок «сb» при повышении напряжения снять нельзя, т.к. из точки «с» происходит срыв в точку «b», сопровождаемый скачком тока 
и изменением знака угла сдвига в цепи. При уменьшении тока происходит срыв из точки «a» в точку «e».
Построить характеристику 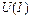для цепи, содержащей сопротивление 
можно провести следующим образом:
1. Строят характеристику .
2. Строят характеристику .
3. Графическим путем находят характеристику 
.
4. Задаются рядом значений тока 
и находят из характеристики 
. Напряжение сети находят по уравнению 
, и строят зависимость .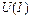
3.3.6 Феррорезонанс токов.
Схема цепи, в которой возможен резонанс токов, приведена на рис.46.а. Как и при резонансе напряжений, пренебрежем потерями в цепи и наличием высших гармоник. Векторная диаграмма цепи представлена на рис.46.б. Из диаграммы:
. (63)
Общий ток 
может быть как отстающим, так и опережающим. На рис.47.а построена ВАХ катушки и конденсаторы 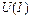путем графического вычитания абсцисс и .
Рис. 46. Цепь с феррорезонансом токов
а) схема цепи; б) векторная диаграмма
Из рис.47.а видно, что при некоторых заданных токах установившийся режим может существовать при трех различных напряжениях 
, 
, 
.
Рис.47. Феррорезонанс токов
а) для идеализированной цепи; б) с учетом потерь
Особая точка «а» является точкой резонанса токов. Отсюда следует, что в данной цепи в отличие от линейных цепей, резонанс можно достичь изменением напряжения. Это явление получило название феррорезонанса токов. В реальной цепи вследствии наличия потерь и высших гармоник, ВАХ видоизменяется (рис.47.б). При постепенном увеличении тока в цепи, а также и при уменьшении его, будут происходить срывы, аналогичные рассмотренным ранее, и также сопровождающиеся изменением знака угла сдвига в цепи. Для получения точек срывов необходимо иметь источник с регулируемым выходным током, а не напряжением.
Практически это можно осуществить, если последовательно с регулируемым источником включить большое линейное сопротивление.
