Одно из самых распространенных применений полупроводниковых элементов состоит в выпрямлении переменного тока.
Для выпрямления применяются электрические вентили с несимметричной характеристикой. Идеальный вентиль в одном направлении должен обладать сопротивлением равным нулю, а в другом – равным бесконечности. ВАХ такого вентиля приведена на рис.58. Включение такого вентиля в цепь переменного тока (рис.57.а) обеспечивает прохождения тока только одного направления (рис.57.б).
Рис.57. Однополупериодный выпрямитель
а) схема выпрямителя, б) диаграмма тока и напряжения
При синусоидальном напряжении 
ток в проводящий период (
) равен 
, а в непроводящий период – нулю.
Рис.58. ВАХ диода
Средний ток (постоянная составляющая):
, (77)
где 
-действующее значение напряжения.
Среднее (выпрямленное) напряжение равно:
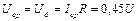. (78)
Рассмотренная схема выпрямления получила название однополупериодного выпрямителя. Основным недостатком этой схемы являются большие пульсации выпрямленного тока, для сглаживания которых применяют индуктивные и емкостные фильтры (рис.59.а,б). Рассмотрим влияние индуктивности L и емкости C на кривые выпрямленных тока и напряжения на конкретном примере.
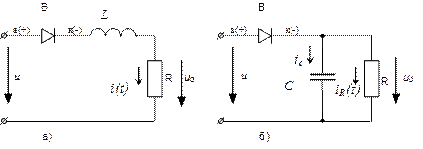
Рис.59. Схема выпрямителя с индуктивным и емкостным фильтром
Пример 13. Для схем 59.а,б требуется рассчитать кривые выпрямленных тока и напряжения. Определить угол пропускания тока (открытого состояния) 
, среднее значение выпрямленных тока и напряжения. Исходные данные: 
; 
=100 Ом;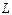 
=1Гн; 
=10-3Ф.
Решение: Для схемы на рис.59.а рассмотрение начнем с нахождения зависимости 
при открытом вентиле. Вентиль открывается при 
,когда 
.Ток определяется в этом случае как переходный ток в цепи «RL» при включении ее на синусоидальное напряжение:
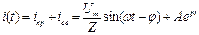, (79)
где 
=329,69 Ом;
= 1,26 рад;
=-100 (1/с).
Постоянная интегрирования 
определяется из начальных условий при 
, 
:
=>, =0,289
В итоге получаем:
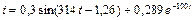. (80)
Результаты расчетов по уравнению сведены в таблицу 11.
Угол пропускания тока определяется моментом изменения знака тока с “+” на “-“:
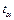=1,474·10-2 с, => 
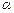= 4,63 рад.
Среднее выпрямленное напряжение:
. (81)
Средний выпрямленный ток:
, (82)
можно определить ток как среднеарифметическое:
. (83)
Расчетные значения тока и напряжения Таблица 11
| t·104 | ωt | L-фильтр | С - фильтр | ||
| i | u | i | u | ||
| 0.209 | 20.9 | ||||
| 0.25 | 0.0097 | 24.8 | 0.248 | 24.8 | |
| 1.6 | 0.5 | 0.0373 | 48.1 | 0.481 | 48.1 |
| 2.4 | 0.75 | 0.0796 | 68.4 | 0.684 | 68.4 |
| 3.2 | 0.132 | 84.4 | 0.84 | 84.4 | |
| 1.25 | 0.191 | 95.1 | 0.95 | 95.1 | |
| 4.8 | 1.5 | 0.252 | 99.8 | 0.99 | 99.8 |
| 5.6 | 1.76 | 0.309 | 98.2 | 0.94 | 94.17 |
| 6.4 | 2.01 | 0.358 | 90.4 | 0.869 | 86.93 |
| 7.2 | 2.26 | 0.395 | 77.05 | 0.8025 | 80.25 |
| 2.51 | 0.417 | 58.7 | 0.74 | 74.08 | |
| 8.8 | 2.76 | 0.422 | 36.8 | 0.68 | 68.38 |
| 9.6 | 3.01 | 0.4089 | 12.5 | 0.63 | 63.12 |
| 10.4 | 3.26 | 0.377 | -12.5 | 0.58 | 58.27 |
| 11.2 | 3.52 | 0.329 | -36.8 | 0.54 | 53.79 |
| 3.76 | 0.266 | -58.7 | 0.5 | 49.65 | |
| 1.28 | 4.02 | 0.193 | -77.05 | 0.46 | 45.8 |
| 1.36 | 4.27 | 0.113 | -90.4 | 0.42 | 42.3 |
| 1.44 | 4.52 | 0.032 | -98.2 | 0.39 | |
| 1.52 | 4.77 | -0.0467 | -99.8 | 0.36 | |
| 1.6 | 5.02 | 0.33 | 33.2 | ||
| 1.68 | 5.27 | 0.307 | 30.7 | ||
| 1.76 | 5.52 | 0.283 | 28.3 | ||
| 1.84 | 5.78 | 0.261 | 26.1 | ||
| 1.92 | 6.03 | 0.241 | 24.17 | ||
| 6.28 | 0.223 | 22.3 | |||
| 2.08 | 6.53 | 0.097 | 24.8 | 0.209 | 20.9 |
Для схемы рис.59.б прежде чем переходить к расчетам необходимо разобраться с физической сущностью процессов. При открытом состоянии вентиля в первую четверть периода напряжение нагрузки (конденсатора) равно напряжению сети и изменяется по закону синусоиды
.
Во вторую четверть периода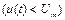 
напряжение на конденсаторе определяется переходной функцией:
, (84)
где 
- принужденная составляющая (в данном случае разрядка конденсатора на резисторе ) 
;
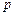- корень характеристического уравнения;
- постоянная интегрирования.
Постоянную интегрирования определим из начальных условий при 
: 
; => 
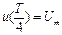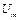= 100.
Разрядка конденсатора продолжается до момента равенства напряжения 
напряжению конденсатора 
, точка “А” на рис.60.
Расчет проводим по четвертям. Для первой четверти напряжение на конденсатора находим по уравнению
.
Далее – по уравнению:
.
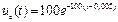Конец второго этапа проще определить графически, в момент равенства напряжений на конденсаторе и входного напряжения:
= 2,066·10-2 с;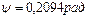 
.
Результаты расчеты сведены в таблицу 11. Угол пропускания: 
= 1,361рад. Среднее значение напряжения
.
Среднее выпрямленное значение тока 
.
По данным таблицы 11 на рис.60 построены кривые выпрямленных тока и напряжения.
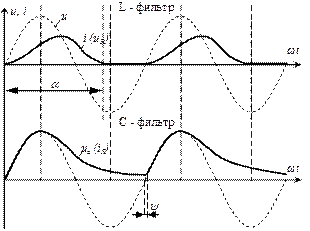
Рис.60. Выпрямленные ток и напряжения с учетом фильтров
Анализируя построенные зависимости, сделаем следующие выводы:
1. Применение любых фильтров уменьшают пульсации выпрямленного тока.
2. Применение L - фильтров снижает величину выпрямленных тока и напряжения, а применение C - фильтров, наоборот, повышает эти величины и при достаточно большой емкости конденсатора можно считать, что выпрямленные значения равны амплитудным значениям.
