Пример 1. Рассмотрим пример умножения матрицы на вектор. Анализируя продолжительность подписки на различные газеты, исследователи охарактеризовали вероятности перехода подписчика от одной газеты к другой в зависимости от продолжительности подписки с помощью соответствующей матрицы. Упрощенный вариант этой матрицы имеет вид:
.
В этой матрице для вероятностей перехода данные структурированы в соответствии с продолжительностью подписки: до одного года, от одного года до двух лет, более двух лет и, наконец, аннулированные подписки.
Предположим, что известно распределение 1000 подписчиков по этим категориям: 500 – принадлежат к 1-й категории, 200 – ко 2-й категории, 300 – к 3-й категории. Тогда вся группа, состоящая из 1000 подписчиков, может быть описана вектором-строкой:
Для того, чтобы определить вероятностное количество подписчиков в каждой из категорий через год, умножим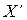 
на матрицу вероятностей перехода P:
.
Вектор, полученный после умножения, показывает, что из первоначальной тысячи подписчиков через год 350, вероятно, будут принадлежать к категории 2, 430- к категории 3 и 220 к категории 4.
Пример 2. Некоторое производственное объединение должно выпустить три вида продукции А1, А2, А3 в количествах, выраженных в процентах к плану, соответственно: 20%, 30% и 50%.
В объединении участвуют четыре предприятия, причем по плану предприятие №1 должно выпустить 30% всей продукции 
А1, 40% всей продукции А2 и 10% всей продукции А3. План для остальных предприятий соответственно следующий:
для предприятия №2 - 40% А1, 10% А2, 30% А3;
для предприятия №3 - 30% А1, 20% А2, 30% А3;
для предприятия №4 - 0% А1, 30% А2, 30% А3.
Требуется найти процент выполнения плана объединения каждым предприятием.
Решение:
Для решения задачи применим операции над матрицами. Обозначим через Хj (j=1,2,3,4) количество продукции выпускаемой по плану j-ым предприятием, тогда получим следующее матричное уравнение:
Выполнив операцию умножения матриц в правой части, будем иметь следующие значения 
: 
.
Матричная алгебра находит большое применение при балансовых расчетах.
Пусть в народном хозяйстве имеется n отраслей. Проанализируем взаимоотношения между ними. Они выражаются в виде поставок друг другу соответствующей продукции (в денежном выражении) в течение некоторого периода, например, одного года.
Для i-й отрасли часть продукции 
идет на потребление первой отраслью, 
– второй и т.д. Вообще 
– материальные затраты i-ой отрасли, потребляемые j-той отраслью 
; 
- внутреннее потребление i-ой отрасли (очень часто 
).
Пусть 
– стоимость товаров i-ой отрасли, идущих на непроизводственное потребление (личное и общественное), накопление и экспорт - “конечный спрос”.
Стоимость всего производства (валовая продукция) i-ой отрасли 
равна сумме соответствующих затрат:
Межотраслевые взаимоотношения записываются в виде системы уравнений:
, где i=1,2,...,n. (1)
Коэффициент 
показывает количество продукции i-ой отрасли, используемой для производства единицы продукции j-той отрасли и считается постоянным в течении планируемого периода.
Подставляя 
в уравнение (1) получим:
, где i=1,2,...,n.
Последнюю систему можно записать в матричной форме:
X = AX + Y (2)
где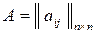 
- матрица прямых затрат.
Уравнение (2) межотраслевых связей можно записать в другом виде:
(3)
Определим, сколько продукции должна выпускать каждая отрасль, если известен ” конечный спрос ” отраслей. Решим матричное уравнение (3) относительно x. Для этого умножим его на обратную матрицу 
слева:
,
.
Матрица 
называется матрицей полных затрат. Элемент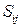 
показывает количество валовой продукции i-той отрасли, затрачиваемое на единицу конечной продукции j-ой отрасли. Матрица S – A называется матрицей косвенных затрат.
Пример 3. Рассмотрим систему двух отраслей экономики: промышленности и сельского хозяйства. Пусть матрица прямых затрат имеет вид:
,
и задан “конечный спрос” каждой отрасли соответственно 330 тыс. руб. и 66 тыс. руб. Каков должен быть валовой выпуск каждой отрасли?
Решение:
Составим матрицу E – A:
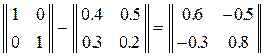
Найдем обратную матрицу для 
с помощью присоединенной матрицы:
Определитель 
,
Матрица полных затрат будет следующей:
Валовой выпуск каждой отрасли составляет: 
Таким образом выпуск промышленности составляет 900 тыс. руб., а сельского хозяйства – 420 тыс. руб.
Матрица косвенных затрат имеет вид:
Модель планирования производства.
Имеется определенное количество изделий (деталей, полуфабрикатов, узлов), которые необходимы для производства других изделий, в том числе конечной продукции. Между отдельными изделиями должны соблюдаться технологические соотношения. Например:
|
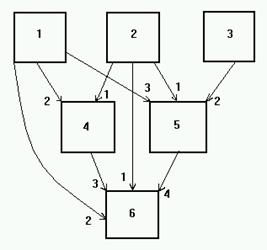
Детали
Узлы
Изделия
Рис. 1.
Стрелки и числа на них показывают, сколько единиц i-го изделия необходимо для изготовления единицы j-го изделия. В общем виде эта информация может быть представлена в виде матрицы затрат:
Если, кроме того, требуется определенное количество деталей и узлов в качестве запасных частей, то для построения математической модели целесообразно также ввести
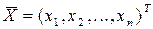- общий выпуск,
- конечный выпуск.
Тогда
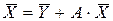
Если задан конечный выпуск, а требуется найти общий выпуск, то задача состоит в том, чтобы разрешить эту систему относительно Х:
(1)
Модель планирования материальных затрат.
1. Расчет общих затрат материалов
Для того чтобы заготовить нужное количество сырья и материалов, необходимо прежде всего рассчитать общие материальные затраты на предприятии.
Обозначим через 
– затраты материалов k-го вида на производство одного изделия j-го вида 
, а через 
- общие затраты материалов k-го вида.
Если объединить все 
в вектор 
, а все в матрицу 
, то имеет место равенство
,
где B – матрица материальных затрат, 
- вектор суммарных материальных затрат.
Подставив Х из (1) получим формулу для вектора суммарных материальных затрат
(2)
2. Расчет суммарной стоимости затраченных материалов.
Если заданы цены всех материалов 
, то суммарная стоимость всех затраченных материалов вычисляется по формуле:
, (3)
где 
.
3. Расчет стоимости затрат по каждому виду материалов.
Если требуется определить стоимость затрат по каждому виду материалов, то целесообразно использовать не вектор, а диагональную матрицу цен, т.е.
.
Вектор 
стоимости затрат по каждому виду материалов получается следующим образом:
(4)
Пример: Рассчитать материальные затраты для схемы, изображенной на рис.1., если заданы:
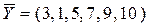- конечный выпуск,
- матрица материальных затрат,
- вектор цен.
Решение:
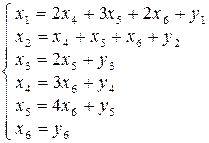
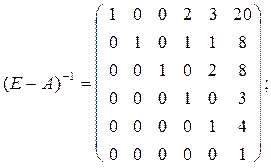
- общий выпуск,
- общая потребность в материалах,
- общая стоимость материальных ресурсов,
- затраты по каждому виду материалов.
Упражнения.
Решить с помощью действий над матрицами следующие задачи.
1. Швейная фирма производит три вида одежды: плащи, пальто и костюмы на пяти фабриках. За планируемый период фирма должна выпустить плащей на сумму 100 тыс. руб. пальто на 40 тыс. руб. и костюмов на 60 тыс. руб. Технологический процесс на фабрике №1 характеризуется тем, что она за планируемый период может выдать 10% плащей, 20% пальто и 60% костюмов от плана фирмы.
Другие фабрики соответственно своим технологическим процессам имеют следующие возможности
фабрика №2 – 10% плащей; 10% пальто; 10% костюмов;
фабрика №3 – 20% плащей; 30% пальто; 20% костюмов;
фабрика №4 – 30% плащей; 40% пальто; 0% костюмов;
фабрика №5 – 30% плащей; 0% пальто; 10% костюмов.
На сколько тысяч рублей продукции должна выполнить план фирмы каждая фабрика?
К решению.
 Распределение
Произв.
| ФАБРИКИ | Непроизводств. потребление в тыс. руб. | ||||
| Плащи | 0,1 | 0,1 | 0,2 | 0,3 | 0,3 | |
| Пальто | 0,2 | 0,1 | 0,3 | 0,4 | ||
| Костюмы | 0,6 | 0,1 | 0,2 | 0,1 |
2. Секция магазина продает продукцию трех видов: A, B и C и двух сортов: первого и второго. В течение определенного месяца проданная продукция состояла из 30% A, 40% B, 30% C, причем 80% продукции A, 70% B и 50% C было первого сорта. Сколько процентов продукции каждого сорта было продано.
3. Дана матрица прямых затрат A. Найти матрицу полных затрат S и матрицу косвенных затрат S-A для:
а)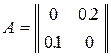 
б) 
в) 
г) 
4. На предприятии имеется три цеха. Сколько продукции должен выпускать каждый цех, если дана матрица прямых затрат A и задана программа выпуска каждого цеха 
:
а) 
б)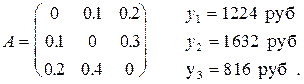 
5. Пусть народное хозяйство состоит из трех отраслей. Коэффициенты прямых затрат, непроизводственное потребление и накопление дано в таблице:
 Распре-деление
Произ-
водство
| ОТРАСЛИ | Непроизводствен-ное потребление и накопление /в тыс. руб./ | Ответ Х | ||
| 1 отрасль | 0,3 | 0,3 | |||
| 2 отрасль | 0,2 | 0,2 | 0,3 | ||
| 3 отрасль | 0,1 | 0,1 | 0,2 |
Исходя из данных таблицы определить матрицу полных затрат, матрицу косвенных затрат и валовый выпуск продукции каждой отрасли.
