Дифференциальные уравнения. Пример 21. Рассмотрим процесс возрастания денежной суммы, положенной в банк при условии начисления 100 rсложных процентов в год

Пример 21. Рассмотрим процесс возрастания денежной суммы, положенной в банк при условии начисления 100 r сложных процентов в год. Пусть обозначает начальную денежную сумму, а – денежную сумму по истечении x лет. Если бы проценты начислялись один раз в год, мы бы имели

где x = 0, 1, 2, 3,.... Если бы проценты начислялись два раза в год (по истечении каждого полугодия), то мы имели бы

где x = 0, 1/2, 1, 3/2,.... Вообще, если проценты начисляются n раз в год и x принимает последовательно значения 0, 1/ n, 2/ n, 3/ n,..., тогда

то есть

Если обозначить 1/ n = h, то предыдущее равенство перепишется так:

Неограниченно увеличивая n (при n ®¥, h ®0) мы в пределе приходим к процессу возрастания денежной суммы при непрерывном начислении процентов:

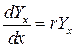то есть при непрерывном изменении x закон возрастания выражен дифференциальным уравнением 1-го порядка. Отметим для четкости, что – неизвестная функция, x – независимая переменная, r – постоянная. Для решения данного уравнения перепишем его следующим образом:

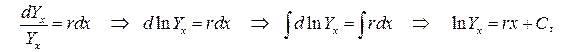
откуда , или ^, где через P обозначено e^C.

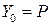Учитывая начальное условие , найдем P: , следовательно, . Решение имеет вид:

Рассмотрим еще одну экономическую задачу. Простейшие макроэкономические модели также приводят к линейным дифференциальным уравнениям 1-го порядка, описывающим изменение дохода или выпуска продукции Y как функций времени.

Пример 22. Пусть национальный доход Y возрастает со скоростью, пропорциональной его величине:

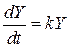и пусть, кроме того, дефицит в расходах правительства прямо пропорционален доходу Y (при коэффициенте пропорциональности q). Дефицит в расходах приводит к возрастанию национального долга D:

Здесь мы считаем переменные Y и D непрерывными и дифференцируемыми функциями времени t. Пусть начальные условия имеют вид Y = Y ₀ и D = D ₀при t = 0. Из первого уравнения мы получаем, учитывая начальные условия, Y = Y ₀ e^k^×^t. Подставляя Y во второе уравнение, получаем dD / dt = qY ₀ e^{k t}. Общее решение этого уравнения имеет вид D = (q / k)× Y ₀e ^k ^× ^t + C, где C = const, которую мы определим из начальных условий. Подставляя начальные условия в полученное решение, мы получаем D ₀= (q / k) Y ₀ + C. Итак, окончательно,

D = D ₀+ (q / k) Y _o(e^k^×^t –1),

то есть, национальный долг возрастает с той же относительной скоростью k, что и национальный доход.

Простейшим дифференциальным уравнением n -го порядка является уравнение

y ⁽ⁿ⁾ = f (x).

Его общее решение можно получить с помощью n интегрирований.

Линейные дифференциальные уравнения 2-го порядка находят применение при изучении, например, экономической модели паутинообразного типа с запасами товаров, в которой скорость изменения цены P зависит от величины запаса. Если спрос и предложение являются линейными функциями цены, то есть

D = a + aP, S = b + bP,

а l есть постоянная, определяющая скорость реакции (то есть изменения цены при изменении запасов товара), то процесс изменения цены описывается дифференциальным уравнением:

+ l(b – a) P = l(a – b).

В качестве частного решения можно взять постоянную

P =` P = (a – b)/(b – a),

имеющую смысл цены равновесия. Отклонение р = P –` P удовлетворяет тогда однородному уравнению

+ l(b – a) р = 0.

Найдем общее решение этого уравнения. Характеристическое уравнение, в котором неизвестная обозначена через k, будет следующее:

k ²+ l(b – a) = 0.

В обычном случае (a <0, b >0, l>0) член l(b – a) положителен. Введем обозначение . Тогда корни характеристического уравнения будут k _1,2 = ± i w. Следовательно, общее решение уравнения (9.10) имеет вид:

р = C cos(w t – e),

где C и e представляют собой произвольные постоянные, которые определяются единственным образом, если заданы начальные условия. Следовательно, присоединив ` P, получим закон изменения цены во времени:

P = ` P + C cos(w t – e).

Разностные уравнения

На практике простейшие разностные уравнения возникают при исследовании например величины банковского вклада. Эта величина является переменной Y_x _, представляющей сумму, которая накапливается по установленному закону при целочисленных значениях аргумента x. Пусть сумма Y ₀положена в банк при условии начисления 100 r сложных процентов в год. Пусть начисление процентов производится один раз в год и x обозначает число лет с момента помещения вклада (x = 0, 1, 2,...). Обозначим величину вклада по истечении x лет через Y_x _. Мы получаем

Y_x = (1 + r) Y_x _–1.

Если начальная сумма составляет Y _0, мы приходим к задаче отыскания решения полученного разностного уравнения, подчиненного начальному условию Y_x = Y ₀при x = 0. Полученное разностное уравнение содержит Y_x и значение этой переменной на один год раньше, т.е. Y_x _–1; в данном случае аргумент x явно не входит в разностное уравнение.

Вообще говоря, обыкновенное разностное уравнение устанавливает связь между значениями функции Y = Y (x), рассматриваемой для ряда равноотстоящих значений аргумента x, но можно без ограничения общности считать, что искомая функция определена для равноотстоящих значений аргумента с шагом, равным единице. Таким образом, если начальное значение аргумента есть x, то ряд его равноотстоящих значений будет x, x + 1, x + 2,..., и в обратном направлении: x, x –1, x –2,.... Соответствующие значения функции будем обозначать Y_x, Y_x ₊₁, Y_x ₊₂,... или Y_x, Y_x _–1, Y_x _–2,.... Определим так называемые разности различных порядков функции Y_x с помощью следующих формул:

Разности первого порядка

D Y_x = Y_x ₊₁– Y_x _,

D Y_x ₊₁= Y_x ₊₂– Y_x _+1,

D Y_x ₊₂= Y_x ₊₃– Y_x _+2,

...............

Разности второго порядка

D² Y_x = D Y_x ₊₁– D Y_x,

D² Y_x ₊₁= D Y_x ₊₂– D Y_x ₊₁,

D² Y_x ₊₂= D Y_x ₊₃– D Y_x ₊₂,

...............

Разности третьего порядка

D³ Y_x = D² Y_x ₊₁– D² Y_x,

D³ Y_x ₊₁= D² Y_x ₊₂– D² Y_x ₊₁,

...............

Обыкновенным разностным уравнением называется уравнение, связывающее значения одного независимого аргумента x, его функции Y_x и разностей различных порядков этой функции D Y_x, D² Y_x, D³ Y_x,.... Такое уравнение можно записать в общем виде следующим образом:

j(x, Y_x, D Y_x, D² Y_x,D³ Y_x, D ⁿY_x ₎ = 0, (1)

которое по форме аналогично дифференциальному уравнению.

Порядком разностного уравнения называется порядок наивысшей разности, входящей в это уравнение. Разностное уравнение (1) часто удобнее записать, пользуясь не разностями неизвестной функции, а ее значениями при последовательных значениях аргумента, то есть выразить D Y_x, D² Y_x, D³ Y_x,... через Y_x, Y_x ₊₁, Y_x ₊₂,.... Уравнение (1) можно привести к одной из двух форм:

y(x, Y_x, Y_x ₊₁,..., Y_x ₊ _n) = 0, (2)

x(x, Y_x, Y_x _–1,..., Y_x _– _n) = 0. (3)

Общее дискретное решение Y_x обыкновенного разностного уравнения n -го порядка представляет функцию x (x = 0, 1, 2,...), содержащую ровно n произвольных постоянных:

Y_x = Y (x, C ₁, C ₂,..., C_n).

Паутинообразная модель. Пусть рынок какого-либо отдельного товара характеризуется следующими функциями спроса и предложения:

D = D (P), S = S (P).

Для существования равновесия цена должна быть такой, чтобы товар на рынке был распродан, или

D (P) = S (P).

Цена равновесия 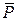задается этим уравнением (которое может иметь множество решений), а соответствующий объем покупок-продаж, обозначаемый через , – следующим уравнением:

Динамическая модель получается при наличии запаздывания спроса или предложения. Простейшая модель в дискретном анализе включает неизменное запаздывание или отставание предложения на один интервал:

D_t = D (P_t) и S_t = S (P_t _–1).

Это может случиться, если для производства рассматриваемого товара требуется определенный период времени, выбранный за интервал. Действие модели таково: при заданном P_t _–1предшествующего периода объем предложения на рынке в текущем периоде будет S (P_t _–1), и величина P_t должна установиться так, чтобы был куплен весь объем предложенного товара. Иными словами, P_t и объем покупок-продаж X_t характеризуются уравнением:

X_t = D (P_t) = S (P_t _–1).

Итак, зная исходную цену P _0, с помощью этих уравнений мы можем получить значения P ₁ и X _1. Затем, используя имеющуюся цену P _1, из соответствующих уравнений получим значения P ₂ и X ₂ и т.д. В общем, изменение P_t характеризуется разностным уравнением первого порядка (одноинтервальное отставание):

D (P_t) = S (P_t _–1).

Решение можно проиллюстрировать диаграммой, представленной на рис. 1, где D и S – соответственно кривые спроса и предложения, а положение равновесия (со значениям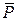и и ) соответствует точке их пересечения Q. Цена в начальный момент времени равна P _0. Соответствующая точка Q ₀на кривой S дает объем предложения в период 1. Весь этот предложенный объем товара раскупается при цене P ₁, заданной точкой Q ₁на кривой D с той же ординатой (X ₁), что и Q ₀. Во второй период времени движение происходит сначала по вертикали от точки Q ₁ к точке на кривой S, дающей X _2, а затем по горизонтали – к точке Q ₂на кривой D. Последняя точка характеризует P ₂. Продолжение этого процесса и дает график паутины, показанный на рис. 5. Цены и объемы (покупок-продаж) в последовательные периоды времени являются соответственно координатами точек Q ₁, Q ₂, Q ₃,... на кривой спроса D. В рассматриваемом случае последовательность точек стремится к Q. При этом точки поочередно располагаются на левой и правой стороне от Q. Следовательно, и значения цены P_t стремятся к ` P, располагаясь поочередно по обе стороны от` P. Точно так же обстоит дело и с объемами покупок - продаж (X_t).

X S

(D; S)

x ₂ Q ₂

` x

x ₃ Q ₃

x ₁ Q ₀ Q ₁

O P ₀ P ₂ ` P P ₃ P ₁ P

Рис. 5.

Решение можно получить алгебраически для случая линейных функций спроса и предложения: D = a + aP, S = b + bP. Значения равновесия ` P и ` X будут заданы уравнениями

` X = a + a ` P = b + b ` P,

то есть

`P = (a – b)/(b – a), `X = (ba – ab)/(b - a). (4)

Дискретная динамическая модель задается уравнением

X_t = a +aP_t = b +bP_t–1. (5)

Ищем сначала решение, дающее равновесие. Для этого положим P_t = `P, X_t = `X для всех значений t:

` X = a +a`P = b +b`P. (6)

Получаем те же значения `P и `X, что и в (4). Следовательно, если в каком-либо периоде существовали цены и объемы, обеспечивающие равновесие, то в динамической модели (5) они сохранятся и в последующих периодах.

Вычтем уравнение (6) из (5) и положим р_t = P_t –`P, x_t = X_t –`X.

Тогда

x_t = aр_t = bр_t_-1. (7)

Уравнения (7) аналогичны (5), за исключением того, что они описывают отклонения от уровней равновесия (теперь уже известно, что таковые существуют). Оба эти уравнения являются разностными уравнениями первого порядка. Положим c = b/a и подставим его в уравнение (7), так что разностное уравнение относительно р_t будет

р_t = cр_t-1. (8)

При данном значении р₀ в момент t = 0 из (8) получаем решение:

р_t = р₀c^t,

или

P_t = `P + (P₀ – `P)c^t.