Потоки платежей. Финансовая рента

Контракты, сделки, коммерческие и производственно-хозяйственные операции часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Отдельные элементы такого ряда, а иногда и сам ряд платежей в целом, называется потоком платежей. Члены потока платежей могут быть как положительными (поступления), так и отрицательными (выплаты) величинами. Поток платежей, все члены которого положительные величины, а временные интервалы между двумя последовательными платежами постоянны, называют финансовой рентой. Ренты делятся на годовые и р -срочные, где р характеризует число выплат на протяжении года. Это дискретные ренты. В финансово-экономической практике встречаются и с последовательностями платежей, которые производятся так часто, что практически их можно рассматривать как непрерывные. Такие платежи описываются непрерывными рентами.

Пример 14. Пусть в конце каждого года в течение четырех лет в банк вносится по 1 млн. рублей, проценты начисляются в конце года, ставка – 5% годовых. В этом случае первый взнос обратится к концу срока ренты в величину 10⁶´1,05³, так как соответствующая сумма была на счете в течение 3 лет, второй взнос увеличится до 10⁶´1,05², так как был на счете 2 года. Последний взнос процентов не приносит. Таким образом, в конце срока ренты взносы с начисленными на них процентами представляют ряд чисел: 10⁶´1,05³; 10⁶´1,05²; 10⁶´1,05; 10⁶. Наращенная к концу срока ренты величина будет равна сумме членов этого ряда. Обобщим сказанное, выведем соответствующую формулу для наращенной суммы годовой ренты. Обозначим: S – наращенная сумма ренты, R – размер члена ренты, i – ставка процентов (десятичная дробь), n – срок ренты (число лет). Члены ренты будут приносить проценты в течение n – 1, n – 2,..., 2, 1 и 0 лет, а наращенная величина членов ренты составит

R (1 + i) ^{n – 1}, R (1 + i) ^{n – 2},..., R (1 + i), R.

Перепишем этот ряд в обратном порядке. Он представляет собой геометрическую прогрессию со знаменателем (1 + i) и первым членом R. Найдем сумму членов прогрессии. Получим: S = R ´((1 + i) ⁿ – 1)/((1 + i) – 1) = R ´((1 + i) ⁿ – 1)/ i. Обозначим S_{n ; i} = ((1 + i) ⁿ – 1)/ i и будем называть его коэффициентом наращения ренты. Если же проценты начисляются m раз в году, то S = R ´((1 + i / m) ^mn – 1)/((1 + i / m) ^m – 1), где i – номинальная ставка процентов.

Величина a_{n ; i} = (1 – (1 + i)^{– n} )/ i называется коэффициентом приведения ренты. Коэффициент приведения ренты при n ®¥ показывает, во сколько раз современная величина ренты больше ее члена:

.

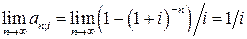Пример 15. Под вечной рентой понимается последовательность платежей, число членов которой не ограничено – она выплачивается в течение бесконечного числа лет. Вечная рента не является чистой абстракцией - на практике это некоторые виды облигационных займов, оценка способности пенсионных фондов отвечать по своим обязательствам. Исходя из сущности вечной ренты можно полагать, что ее наращенная сумма равна бесконечно большой величине, что легко доказать по формуле:

R ´((1 + i) ⁿ – 1)/ i ® ¥ при n ® ¥.

Коэффициент приведения для вечной ренты a_n;i ® 1/ i, откуда A = R / i, т. е. современная величина зависит только от величины члена ренты и принятой ставки процентов.

Производная

Предельный анализ в экономике. Эластичность функции

В экономических исследованиях для обозначения производных часто пользуются специфической терминологией. Например, если f (x) есть производственная функция, выражающая зависимость выпуска какой-либо продукции от затрат фактора x, то f' (x) называют предельным продукт ом; если g (x) есть функция издержек, т. е. функция g (x)выражает зависимость общих затрат от объема продукции x, то g' (x) называют предельными издержками.

Предельный анализ в экономике – совокупность приемов исследования изменяющихся величин затрат или результатов при изменении объемов производства, потребления и т.п. на основе анализа их предельных значений. Большей частью плановые расчеты, основывающиеся на обычных статистических данных, ведутся в форме суммарных показателей. При этом анализ заключается главным образом в вычислении средних величин. Однако в некоторых случаях оказывается необходимым более детальное исследование с учетом предельных значений. Например, при выяснении издержек производства зерна в районе на перспективу принимают во внимание, что издержки могут быть различными в зависимости, при прочих равных условиях, от предполагаемых объемов сбора зерна, так как на вновь вовлекаемых в обработку худших землях издержки производства будут выше, чем по району в среднем.

Если зависимость между двумя показателями v и x задана аналитически: v = f (x) – то средняя величина представляет собой отношение v/x, а предельная – производную .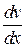

Нахождение производительности труда. Пусть известна функция u = u (t), выражающая количество произведенной продукции u за время работы t. Вычислим количество произведенной продукции за время D t = t ₁ - t ₀: D u = u (t ₁) - u (t ₀) = u (t ₀+D t) - u (t ₀). Средней производительностью труда называется отношение количества произведенной продукции к затраченному времени, т.е. z _ср.= D u /D t.

Производительностью труда рабочего z (t ₀) в момент t ₀ называется предел, к которому стремится z _ср. при D t ®0: 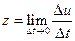. Вычисление производительности труда, таким образом, сводится к вычислению производной: z (t ₀) = u '(t ₀).

Издержки производства K однородной продукции есть функция количества продукции x. Поэтому можно записать K = K (x). Предположим, что количество продукции увеличивается на D х. Количеству продукции x + D х соответствуют издержки производства K (x + D х). Следовательно, приращению количества продукции D х соответствует приращение издержек производства продукции D K = K (x + D х) – K (x).

Среднее приращение издержек производства есть D K /D х. Это приращение издержек производства на единицу приращения количества продукции.

Предел 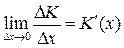называется предельными издержками производства.

Если обозначить через u (x) выручку от продажи x единиц товара, то 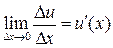и называется предельной выручкой.

С помощью производной можно вычислить приращение функции, соответствующее приращению аргумента. Во многих задачах удобнее вычислять процент прироста (относительное приращение) зависимой переменной, соответствующий проценту прироста независимой переменной. Это приводит к понятию эластичности функции (иногда ее называют относительной производной). Итак, пусть дана функция y = f (x), для которой существует производная y ¢ = f ¢(x). Эластичностью функции y = f (x) относительно переменной x называют предел

.

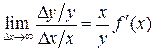Его обозначают .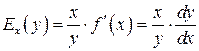

Эластичность относительно x есть приближенный процентный прирост функции (повышение или понижение), соответствующий приращению независимой переменной на 1%. Экономисты измеряют степень чуткости, или чувствительности, потребителей к изменению цены продукции, используя концепцию ценовой эластичности. Для спроса на некоторые продукты характерна относительная чуткость потребителей к изменениям цен, небольшие изменения в цене приводят к значительным изменениям в количестве покупаемой продукции. Спрос на такие продукты принято называть относительно эластичным или просто эластичным. Что касается других продуктов, потребители относительно нечутки к изменению цен на них, то есть существенное изменение в цене ведет лишь к небольшому изменению в количестве покупок. В таких случаях спрос относительно неэластичен или просто неэластичен. Термин совершенно неэластичный спрос означает крайний случай, когда изменение цены не приводит ни к какому изменению количества спрашиваемой продукции. Примером может служить спрос больных острой формой диабета на инсулин или спрос наркоманов на героин. И наоборот, когда при самом малом снижении цены покупатели увеличивают покупки до предела своих возможностей - тогда мы говорим, что спрос является совершенно эластичным.

Экстремум функции

В естествознании, технике и экономике часто приходится иметь дело с эмпирическими формулами, т.е. формулами, составленными на основе обработки статистических данных или результатов опытов. Одним из распространенных приемов построения таких формул является метод наименьших квадратов. Изложим идею этого способа, ограничиваясь случаями линейной и квадратичной зависимости. Пусть требуется установить зависимость между двумя величинами x и y, например, между стоимостью потребляемого сырья и стоимостью выпущенной продукции. Произведем обследование n видов продукции и представим результаты исследования в виде таблицы:

x	x 1	x 2	...	xn
y	y 1	y 2	...	yn

Из анализа таблицы нелегко обнаружить наличие и характер зависимости между x и y. Поэтому обратимся к графику. Допустим, что точки, взятые из таблицы (опытные точки) группируются около некоторой прямой линии. Тогда можно предположить, что между x и y существует линейная зависимость 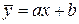, где a и b – коэффициенты, подлежащие определению, 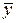– теоретическое значение ординаты. Проведя прямую “на глаз”, можно графически найти b и a = tga, однако это будут весьма неточные результаты. Для нахождения a, b применяют метод наименьших квадратов.

Перепишем уравнение искомой прямой в виде 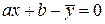. Точки, построенные на основе опытных данных, вообще говоря, не лежат на этой прямой. Поэтому если подставить в уравнение прямой вместо x и 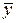заданные величины x_i и y_i, то окажется, что левая часть уравнения равна какой-то малой величине 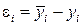; а именно: для первой точки ax ₁ + b – y ₁ = e_1, для второй – ax ₂ + b – y ₂ = e_2, для последней – ax_n + b – y_n = e _{n .} Величины e₁, e₂,..., e _n, не равные нулю, называются погрешностями. Геометрически это разность между ординатой точки на прямой и ординатой опытной точки с той же абсциссой. Погрешности зависят от выбранного положения прямой, т.е. от a и b. Требуется подобрать a и b таким образом, чтобы эти погрешности были возможно меньшими по абсолютной величине. Способ наименьших квадратов состоит в том, что a и b выбираются из условия, чтобы сумма квадратов погрешностей 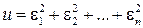была минимальной. Если эта сумма квадратов окажется минимальной, то и сами погрешности будут в среднем малыми по абсолютной величине. Подставим в выражение для u вместо e _i их значения.

u = (ax ₁ + b – y ₁)² + (ax ₂ + b – y ₂)² +... + (ax_n + b – y_n)², или u = u (a, b), где x_i, y_i известные величины, a и b – неизвестные, подлежащие определению. Выберем a и b так, чтобы u (a, b) имело наименьшее значение.

Необходимые условия экстремума 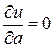, 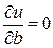. Имеем:

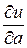= 2(ax ₁ + b – y ₁) x ₁ +... +2(ax ₁ + b – y ₁) x_{n ,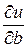} = 2(ax ₁ + b – y ₁) +... + 2(ax ₁ + b – y ₁). Получаем систему:

.

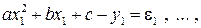
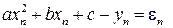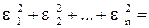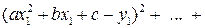
Эта система называется нормальной системой метода наименьших квадратов. Из нее находим a и b и затем подставляем их в эмпирическую формулу ` y = ax + b. Пусть теперь точки на графике располагаются вблизи некоторой параболы так, что между x и y можно предположить квадратичную зависимость:` y = ax ² + bx + c, тогда . Тогда u = = 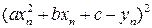. Здесь u = u (a, b, c) – функция трех независимых переменных a, b, c. Необходимые условия экстремума 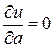, , 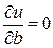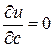в этом случае примут следующий вид:

.

Получили нормальные уравнения способа наименьших квадратов для квадратичной зависимости ` y = ax ² + bx + c, коэффициенты которой находим, решая систему трех линейных уравнений с тремя неизвестными.

Отыскание уравнения прямой по эмпирическим данным называется выравниванием по прямой, а отыскание уравнения параболы – выравниванием по параболе. В экономических расчетах могут встретиться также и другие функции. Довольно часто встречаются эмпирические формулы, выражающие обратно пропорциональную зависимость, графически изображаемую гиперболой. Тогда говорят о выравнивании по гиперболе и т.д.

Метод наименьших квадратов оказывается весьма эффективным при исследовании качества промышленной продукции в зависимости от определяющих его факторов на основе статистических данных текущего контроля качества продукции, в задачах моделирования потребительского спроса.

Пример 16. Темпы роста y производительности труда по годам в промышленности республики приведены в таблице.

x
y

Предполагая, что зависимость y от x линейная: y = ax + b, найти a и b.

Решение. Вычислим коэффициенты нормальной системы уравнений:

.

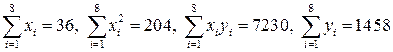Следовательно, имеем систему 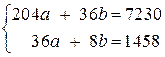, решая которую, получим: a» 15,93; b» 110,57. Итак, получили уравнение искомой прямой: y = 15,93 x + 110,57.

Интегралы

Использование интегралов в экономических расчетах

Пример 17. Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией

f (t) = 3/(3 t +1) + 4.

Решение. Если непрерывная функция f (t) характеризует производительность труда рабочего в зависимости от времени t, то объем продукции, произведенной рабочим за промежуток времени от t ₁ до t ₂ будет выражаться формулой

V = .

В нашем случае

V = 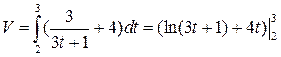= ln 10 + 12 – ln 7 – 8 = ln 10/7 + 4.

Пример 18. Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией f (t) = 2 t + 5.

Решение. Имеем:

V = .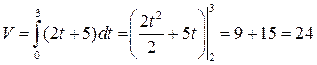

Пример 19. Пусть сила роста описывается некоторой непрерывной функцией времени d _t = f (t), тогда наращенная сумма находится как

,

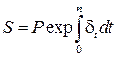а современная величина платежа .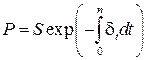

Если, в частности, d _t является линейной функцией времени:

d _t = d₀ + at, где d₀ – величина силы роста для t = 0, a – годовой прирост, то

;

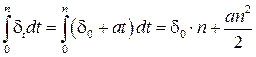множитель наращения 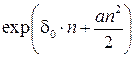. Если сила роста изменяется по геометрической прогрессии , где d₀ – начальное значение процентной ставки, a – годовой коэффициент роста, тогда

;

множитель наращения .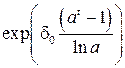

Предположим, что начальный уровень силы роста равен 8%, процентная ставка ежегодно увеличивается на 20% (a=1,2), срок ссуды 5 лет. Множитель наращения в этом случае составит .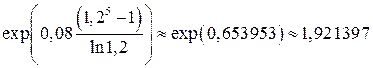

Пример 20. Выше при анализе непрерывных потоков платежей предполагалось, что годовая сумма ренты R равномерно распределяется на протяжении года. На практике, особенно в инвестиционных процессах, этот поток может существенно изменяться во времени, следуя какому-либо закону. Если этот поток непрерывен и описывается некоторой функцией R_t = f (t), то общая сумма поступлений за время n равна .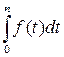

В этом случае наращенная по непрерывной ставке за период от 0 до n сумма составит:

.

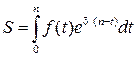Современная величина такого потока равна

.

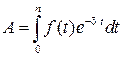Пусть функция потока платежей является линейной: , где 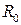– начальная величина платежа, выплачиваемого за единицу времени, в которой измеряется срок ренты. Вычислим современную величину A, пользуясь правилами интегрирования определенного интеграла:

.

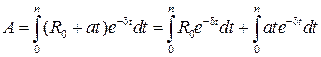Обозначим , .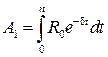

Имеем: .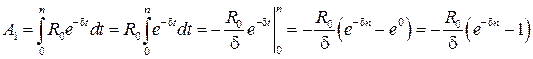

.

Вычислим неопределенный интеграл

по частям: u = t, 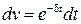Þ du = dt, 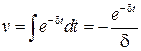, тогда .

Следовательно,

.

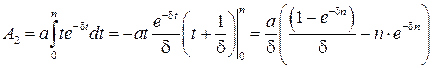Итак, исходный интеграл

.
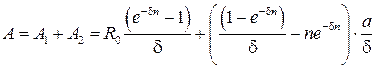