Метод статистического моделирования (или метод Монте-Карло) – это способ исследования поведения вероятностных систем (технических, экономических и т.д.) в условиях, когда не известны в полной мере внутренние взаимодействия в этих системах.
Метод заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Одно такое воспроизведение функционирования системы называют реализацией или испытанием. После каждого испытания регистрируют совокупность параметров, характеризующих случайный исход реализации. Метод основан на многократных испытаниях построенной модели с последующей статистической обработкой полученных данных с целью определения числовых характеристик рассматриваемого процесса в виде статистических оценок его параметров. Процесс моделирования функционирования приборной системы сводится к машинной имитации изучаемого процесса со всеми сопровождающими его случайностями.
Основой метода статистического моделирования является закон больших чисел, который доказывает для различных условий сходимость по вероятности средних значений результатов большого числа наблюдений к некоторым постоянным величинам.
Под законом больших чисел понимают ряд теорем. Например, одна из теорем Л.Л. Чебышева формулируется так: «При неограниченном увеличении числа независимых испытаний n среднее арифметическое свободных от систематических ошибок и равноточных результатов наблюдений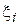 
случайной величины x, имеющей конечную дисперсию D (x), сходится по вероятности к математическому ожиданию M (x) этой случайной величины». Это можно записать в следующем виде:
(8.1)
где e – сколь угодно малая положительная величина.
Теорема Бернулли формулируется так: «При неограниченном увеличений числа независимых испытаний в одних и тех же условиях частота P *(A) наступления случайного события A сходится по вероятности к его вероятности P, т.е.
(8.2)
Согласно данной теореме, для получения вероятности какого-либо события, например вероятности состояний некоторой системы 
, вычисляют частоты 
для одной реализации (испытания), далее проводят подобные вычисления для числа реализаций, равного n. Результаты усредняют и этим самым с некоторым приближением, получают искомые вероятности состояний системы. На основании вычисленных вероятностей определяют другие характеристики системы. Чем больше число реализаций n, тем точнее результаты вычисления искомых величин (вероятностей состояний системы).
Решение любой задачи методом статистического моделирования состоит в:
- разработке и построении структурной схемы процесса, выявлении основных взаимосвязей;
- формальном описании процесса;
- моделировании случайных явлений (случайных событий, случайных величин, случайных функций), сопровождающих функционирование исследуемой системы;
- моделировании (с использованием данных, полученных на предыдущем этапе) функционирования системы – воспроизведении процесса в соответствии с разработанной структурной схемой и формальным описанием;
- накоплении результатов моделирования, их статистической обработке, анализе и обобщении.
В отличие от описанных ранее математических моделей, результаты которых отражали устойчивое во времени поведение системы, результаты, получаемые при статистическом моделировании, подвержены экспериментальным ошибкам. Это означает, что любое утверждение, касающееся характеристик моделируемой системы, должно основываться на результатах соответствующих статистических проверок.
Экспериментальные ошибки при статистическом моделировании в значительной степени зависят от точности моделирования случайных явлений, сопровождающих функционирование исследуемой системы.
При изучении вероятностных систем случайные явления могут интерпретироваться в виде случайных событий, случайных величин и случайных функций. Следовательно, моделирование случайных явлений сводится к моделированию случайных событий, случайных величин и случайных функций. Так как случайные события и случайные функции могут быть представлены через случайные величины, то и моделирование случайных событий и случайных функций производится с помощью случайных величин.
