Дано: в системе имеется n каналов, на которые поступает поток заявок с интенсивностью l. Поток обслуживаний имеет интенсивность m. Заявка, заставшая систему занятой, сразу же покидает ее.
Найти: абсолютную и относительную пропускную способность СМО; вероятность того, что заявка, пришедшая в момент времени t, получит отказ; среднее число заявок, обслуживаемых одновременно (или, другими словам, среднее число занятых каналов).
Решение. Состояние системы S (СМО) нумеруется по максимальному числу заявок, находящихся в системе (оно совпадает с числом занятых каналов):
S 0 – в СМО нет ни одной заявки;
S 1 – в СМО находится одна заявка (один канал занят, остальные свободны);
S 2 – в СМО находится две заявки (два канала заняты, остальные свободны);
...
Sn – в СМО находится n заявок (все n каналов заняты).
Граф состояний СМО представлен на рис. 4.7
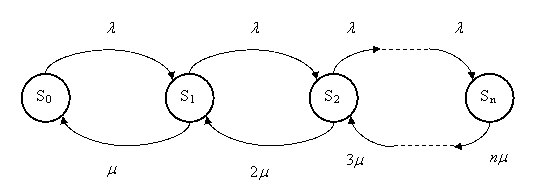
Рис. 4.7. Граф состояний для n -канальной СМО с отказами
Из состояния S 0 в состояние S 1 систему переводит поток заявок с интенсивностью l (как только приходит заявка, система переходит из S 0 в S 1). Если система находилась в состоянии S 1 и пришла еще одна заявка, то она переходит в состояние S 2 и т.д.
Пусть система находится в состоянии S 1 (работает один канал). Он производит m обслуживаний в единицу времени. Поэтому дуга перехода из состояния S 1 в состояние S 0 нагружена интенсивностью m. Пусть теперь система находится в состоянии S 2 (работают два канала). Чтобы ей перейти в S 1, нужно, чтобы закончил обслуживание первый канал, либо второй. Суммарная интенсивность их потоков равна 2m и т.д.
Выходные характеристики (характеристики эффективности) данной СМО определяются следующим образом.
Абсолютная пропускная способность:
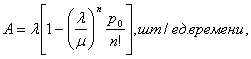
где n – количество каналов СМО; p 0 – вероятность нахождения СМО в начальном состоянии, когда все каналы свободны (финальная вероятность нахождения СМО в состоянии S 0).
Для того чтобы написать формулу для определения p 0, рассмотрим рис. 4.8.
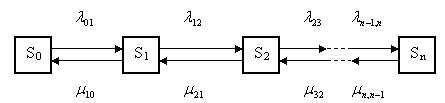
Рис. 4.8. Граф состояний для схемы «гибели и размножения»
Граф, представленный на этом рисунке, называют графом состояний для схемы «гибели и размножения».
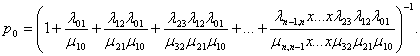
Остальные финальные вероятности состояний СМО запишутся следующим образом.
Вероятность того, что СМО находится в состоянии S 1, когда один канал занят:
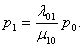
Вероятность того, что СМО находится в состоянии S 2, т.е. когда два канала заняты:
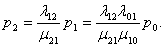
Вероятность того, что СМО находится в состоянии Sn, т.е. когда все каналы заняты.
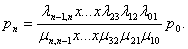
Теперь для n -канальной СМО с отказами
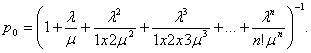
При этом
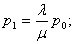
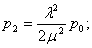
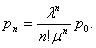
Относительная пропускная способность (средняя доля заявок, обслуживаемых системой):
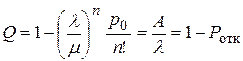 .
.
Вероятность отказа (вероятность того, что заявка покинет СМО необслуженной):
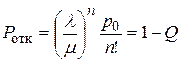 .
.
Среднее число занятых каналов (среднее число заявок, обслуживаемых одновременно):
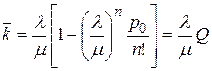 .
.






