1. Напишіть, використовуючи мову логіки предикатів, такі речення:
а) ” число х більше 2 ”;
б) ” х сестра у ”;
в) ” діагоналі ромба перпендикулярні ”;
г) ”кожне явище має свою причину ”.
2. Перекладіть природною мовою такі висловлювання логіки предикатів:
а) ДОРІВНЮВАТИ (х, 10);
б) ЛЮБИТИ (мама (Каті), гімнастика);
в) БІЛЬШЕ (плюс (х, 1), 1).
3. Змінні функції ” х > у ” набувають значень на множині
{ 2,3,4 }; Р  , Р
, Р  – предикати, що задаються цією функцією відповідно при алфавітному і зворотному йому порядках. Необхідно встановити:
– предикати, що задаються цією функцією відповідно при алфавітному і зворотному йому порядках. Необхідно встановити:
а) область визначення предикатів Р  і Р
і Р  ;
;
б) значення істинності Р  (3,4) і Р
(3,4) і Р  (3,4).
(3,4).
4. Визначте еквівалентність таких предикатів:
а) х 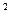 = х і х = 1;
= х і х = 1;
б) х 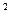 = 1 і х = 1;
= 1 і х = 1;
в) х  = 1 і х = 1.
= 1 і х = 1.
5. Запишіть такі висловлювання, використовуючи логіку предикатів:
а) будь-яке парне додатне число;
б) існує таке число х, що х 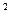 + 1 = 10;
+ 1 = 10;
в) для будь-якого х завжди х + 0 = х.
6. Вкажіть вільні та пов’язані входження кожної зі змінних у таких формулах:
а)  х Р (х,у)
х Р (х,у) 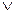
 х Q (х,у);
х Q (х,у);
б)  у Q (х,у)
у Q (х,у) 
 х Р (х,у);
х Р (х,у);
в)  х [(Р (х,у)
х [(Р (х,у)  Q (у))
Q (у)) 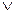
 у Р (х,у) ].
у Р (х,у) ].
7. Наведені висловлювання для предиката Р(х,у), де " х сестра у ”, сформулювати природною мовою, визначивши їх значення істинності:
а)  у
у  х Р (х,у); г)
х Р (х,у); г)  у
у  х Р (х,у);
х Р (х,у);
б)  х
х  у Р (х,у); д)
у Р (х,у); д)  х
х  у Р (х,у);
у Р (х,у);
в)  х
х  у Р (х,у); е)
у Р (х,у); е)  х
х  у Р (х,у).
у Р (х,у).
8. Предикат 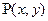 задано на предметній області D={а, в} такою матрицею:
задано на предметній області D={а, в} такою матрицею:
| х | а | а | в | в |
| у | а | в | а | в |
| Р(х,у) | Х | І | І | І |
Яка з наведених формул визначає цей предикат?
а)  х
х  у Р (х,у); г)
у Р (х,у); г)  у
у  х Р (х,у);
х Р (х,у);
б)  у
у  х Р (х,у); д)
х Р (х,у); д)  у Р (а;у);
у Р (а;у);
в)  х Р (х,а); є)
х Р (х,а); є)  х
х  у Р (х,у);
у Р (х,у);
9. Визначте вільні та пов’язані входження змінних у такі формули, що містять предикати Р і  :
:
а)  х
х  Р (х
Р (х  , х
, х  );
);
б)  х
х  (
( х
х  Р (х
Р (х  , х
, х  )
)  Р (х
Р (х  , х
, х  ));
));
в)  х
х  (
( х
х  Р (х
Р (х  , х
, х  )
)  Р (х
Р (х  , х
, х  ));
));
г)  х
х 
 х
х  Р (х
Р (х  , х
, х  )
)  Q (х
Q (х  );
);
д)  х
х  Р (х
Р (х  , х
, х  )
) 
 х
х  Р (х
Р (х  , х
, х  ).
).
10. Знайдіть значення істинності таких предикатних виразів:
а) P (a, f (a))  P (b, f (b));
P (b, f (b));
б)  х
х  y P (x,y)
y P (x,y)  P (f (x), f (y))
P (f (x), f (y))
на предикатній області D = { 3,4 } при значенні функціональних символів:
f(a) = 4, f(b) = 3; предикатів P(3,3,) = І, P(3,4,) =
= І, P(4,3,) = І, P(4,4,) = Х.
11. Оцінити формулу  x P(x)
x P(x)  Q (f(x),a) на інтерпретації при: D = { 1,2 };
Q (f(x),a) на інтерпретації при: D = { 1,2 };
a = 1; f (1) = 2; f (2) = 1;P (1) = Х; P (2) = І; Q (1,1) = = І; Q (1,2) = І;
Q (2,1) = Х; Q (2,2) = І.
12. Визначити рівносильність формул  x
x  P(x
P(x  ),
),  x
x  P(x
P(x  ) на двохелементній множині M = { a,b }.
) на двохелементній множині M = { a,b }.
13. Визначити рівносильність формул F=P(x1, x2)Ú P(x1, x3) і G=P(x  ,x
,x  )
) 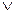 P(x
P(x  ,x
,x  ), які задані на множині M = { a,b } предикатами Q
), які задані на множині M = { a,b } предикатами Q  (x,y) та Q
(x,y) та Q  (x,y), наведеними в таблицях
(x,y), наведеними в таблицях
| х | у | 
| х | у | 
| |

| 
| Х | 
| 
| х | |

| 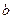
| І | 
| 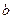
| І | |
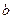
| 
| І | 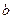
| 
| Х | |
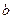
| 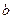
| Х | 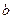
| 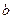
| І |
14. Для заданих предикатів  х (Р (х)
х (Р (х) 
 Q (х)) і
Q (х)) і

 z (Р (z)
z (Р (z)  Q (у)) встановити їх еквівалентність.
Q (у)) встановити їх еквівалентність.
15. Винести за дужки квантори:
а)  х Р (х,у)
х Р (х,у) 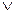 (
(  х Q (х)
х Q (х) 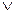
 у Q (у));
у Q (у));
б)  х
х  у Р (х,у)
у Р (х,у) 
 х
х  у (Q (х, z)
у (Q (х, z) 
 у Р (х,у));
у Р (х,у));
в)  х Р (х,у)
х Р (х,у)  (
(  у Р (у)
у Р (у) 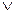 Q).
Q).
16. Довести загальнозначущість формули
 х Р (х)
х Р (х) 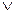
 у
у  Р (у).
Р (у).
17. Довести суперечливість формули
 х Р (х)
х Р (х) 
 у
у  Р (у).
Р (у).
18. Показати, що комутативні властивості для виразу
 х
х  у Р (х,у)
у Р (х,у) 
 у
у  х Р (х,у)
х Р (х,у)
не виконуються.
19. Довести, що:
а) ├  x (А → В) → (
x (А → В) → ( x А →
x А →  x В);
x В);
б) А,  x А → В ├
x А → В ├  x В;
x В;
в) ├  x1
x1  x2 …
x2 …  xm А → А;
xm А → А;
г)  x (А → В)
x (А → В)  (А →
(А →  x В);
x В);
д)  x (В → А)
x (В → А)  (
(  х В → А);
х В → А);
е)  x (А
x (А  D) → (
D) → ( x А
x А 
 x В).
x В).
Коментарі. Основні відомості з логіки предикатів, кванторів і формул логіки предикатів, викладені в цьому розділі, dзяті з [9, 20], рівносильність формул логіки предикатів і логічні висновки ‒ з [1, 7, 21], а закони, тотожності логіки предикатів і випереджені нормальні форми випливають із [20, 28].






