Із таблиці істинності (табл. 1.2.2) випливає, що висловлювання A  B є імплікацією (умовним реченням), набуває значення хибності тоді і тільки тоді, коли A – істинне, а B – хибне. В утвореному реченні A
B є імплікацією (умовним реченням), набуває значення хибності тоді і тільки тоді, коли A – істинне, а B – хибне. В утвореному реченні A  B висловлювання A називають засновком (умовою), а B – наслідком
B висловлювання A називають засновком (умовою), а B – наслідком
(висновком). Природною мовою причинно-наслідковий зв'язок між висловлюваннями A і B описують такими зворотами: “ Якщо A, то B ”, “ A є достатньою підставою для B ”і таке інше.
Приклад 1.3.1. Для висловлювання “ Якщо іде дощ, то щоб не змокнути, я відкриваю парасольку над головою ” записати формулу висловлювань і побудувати таблицю істинності.
Розв’язання. Для цього висловлювання введемо атоми: A – “ йде дощ ”, B – “ щоб не змокнути, я відкриваю парасольку над головою ”.
Тоді цьому висловлюванню відповідатиме формула A  B, а результати інтерпретації поданого висловлювання наведені в таблиці істинності (табл. 1.3.1).
B, а результати інтерпретації поданого висловлювання наведені в таблиці істинності (табл. 1.3.1).
Таблиця 1.3.1 – Інтерпретація результатів
| A | B | A  B B
| Результат |
| X | X | I | залишуся сухим |
| X | I | I | залишуся сухим |
| I | X | X | намокну |
| I | I | I | залишуся сухим |
За допомогою імплікації можна формально виразити поняття достатньої та необхідної умови. Наприклад, якщо A  B, то це означає, що “ A є достатньою умовою для B ” і одночасно, що “ B є необхідною умовою для А ”. Тобто необхідність для А можна записати у формі “ В тільки, якщо А ” - A
B, то це означає, що “ A є достатньою умовою для B ” і одночасно, що “ B є необхідною умовою для А ”. Тобто необхідність для А можна записати у формі “ В тільки, якщо А ” - A  B. Твердження “ А є необхідною і достатньою умовою для В ” еквівалентне подвійній імплікації
B. Твердження “ А є необхідною і достатньою умовою для В ” еквівалентне подвійній імплікації  . Покажемо це за допомогою таблиці істинності (табл. 1.3.2).
. Покажемо це за допомогою таблиці істинності (табл. 1.3.2).
Таблиця 1.3.2

| 
| 
| 
| 
|
| X | X | I | I | I |
| X | I | I | X | X |
| I | X | X | I | X |
| I | I | I | I | I |
Із таблиці істинності бачимо, що висловлювання  істинне тоді і тільки тоді, коли висловлювання
істинне тоді і тільки тоді, коли висловлювання  та
та  істинні або хибні одночасно, що й відповідає еквіваленції. Але не за всіх умовних висловлювань буває так.
істинні або хибні одночасно, що й відповідає еквіваленції. Але не за всіх умовних висловлювань буває так.
Приклад 1.3.2. У висловлюванні“ Якщо число n парне ( ), то n ділиться націло на 4 (
), то n ділиться націло на 4 ( ) ” показати необхідність і достатність умови й записати її істинність через знак імплікації.
) ” показати необхідність і достатність умови й записати її істинність через знак імплікації.
Розв’язання. Оскільки жодне непарне число на 4 не ділиться, то це умова  є необхідною, але в той самий час є парні числа, які не діляться націло на 4, наприклад 10. Тобто очевидним є відсутність достатності умови у заданому висловлюванні. Тому задане висловлювання за умовою
є необхідною, але в той самий час є парні числа, які не діляться націло на 4, наприклад 10. Тобто очевидним є відсутність достатності умови у заданому висловлюванні. Тому задане висловлювання за умовою  хибне, а правильною імплікацією для заданої умови буде
хибне, а правильною імплікацією для заданої умови буде  .
.
Приклад 1.3.3. У висловлюванні “ Якщо геометрична фігура – квадрат ( ), то вона – прямокутник, у якого всі сторони рівні між собою (
), то вона – прямокутник, у якого всі сторони рівні між собою ( ) ” показати необхідність і достатність умови і записати її через знак логічного зв’язку.
) ” показати необхідність і достатність умови і записати її через знак логічного зв’язку.
Розв’язання. За умовою квадрат ( ) – це прямокутник, у якого всі сторони рівні між собою (
) – це прямокутник, у якого всі сторони рівні між собою ( ), що є необхідною і достатньою умовою для виконання
), що є необхідною і достатньою умовою для виконання  , і тому логічним зв’язком між даними висловлюваннями буде еквіваленція
, і тому логічним зв’язком між даними висловлюваннями буде еквіваленція  .
.
З умовним висловлюванням  зв’язані ще три висловлювання: конверсія, інверсія та контрапозиція. Вони визначаються таким чином:
зв’язані ще три висловлювання: конверсія, інверсія та контрапозиція. Вони визначаються таким чином:  – конверсія висловлювання
– конверсія висловлювання  ;
; 


 – інверсія висловлювання
– інверсія висловлювання  ;
; 
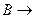

 – контрапозиція висловлювання
– контрапозиція висловлювання  .
.
Приклад 1.3.4. Для висловлювання “ Якщо він добре грає у футбол, то він популярний ” знайти конверсію, інверсію та контрапозицію.
Розв’язання. Відповідно до їх означення шукані результати матимуть такий зміст.
Конверсія – “ Якщо він популярний, то він добре грає у футбол ”. Інверсія – “ Якщо він недобре грає у футбол, то він непопулярний ”. Контрапозиція – “ Якщо він непопулярний, то він недобре грає у футбол ”.
Означення 1.3.1. Висловлювання  ~
~  називають еквівалентністю (еквіваленцією) тоді і тільки тоді, коли висловлювання
називають еквівалентністю (еквіваленцією) тоді і тільки тоді, коли висловлювання  і
і  хибні або істинні одночасно. Ця операція відповідає у природній мові зворотам:
хибні або істинні одночасно. Ця операція відповідає у природній мові зворотам:
“ тоді і тільки тоді, коли ”, “ для того, щоб ”, “ необхідно і достатньо ”.
Із таблиці істинності (табл. 1.3.1) випливає, що вираз  ~
~  еквівалентний виразу
еквівалентний виразу  . Це свідчить про те, що логічна еквівалентність зображує імплікацію в обох напрямках. Виходячи з означення еквівалентності, формула для неї має такий вигляд:
. Це свідчить про те, що логічна еквівалентність зображує імплікацію в обох напрямках. Виходячи з означення еквівалентності, формула для неї має такий вигляд:  ~
~ 




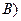 .
.
Приклад 1.3.5. Записати у вигляді формули логіки висловлювань і визначити істинне значення таких висловлювань:
1. “ Для того щоб 4: 2 = 2, необхідно і достатньо, щоб 4 - 2 = 2 ”. 2. “ 4: 2 = 3 рівнозначне 4 - 2 = 1 ”.
Розв’язання. Вводимо позначення атомів:
A = 4: 2 = 2; B = 4 - 2 =2;
C = 4: 2 = 3; D = 4 - 2 = 1.
Тоді можна сказати, що висловлювання 1 відповідає формулі  ~
~  , а висловлювання 2 – формулі
, а висловлювання 2 – формулі 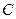 ~
~  . Якщо атоми
. Якщо атоми  і
і  істинні, а атоми
істинні, а атоми 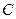 і
і  хибні, то визначення істинності значень складних висловлювань таке:
хибні, то визначення істинності значень складних висловлювань таке:
 ~
~ 
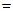 I ~ I = I;
I ~ I = I; 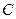 ~
~  = X ~ X = I.
= X ~ X = I.
Прочитання формул складних висловлювань може бути неоднозначним, якщо не ввести дужки, що вказують, у якому порядку зв’язуються між собою символи. Послідовність виконання (пріоритет операцій) у логіці висловлювань є такою:  ,
,  ,
,  ,
,  , ~. Наприклад, такі вирази без дужок дорівнюють формулам із дужками
, ~. Наприклад, такі вирази без дужок дорівнюють формулам із дужками
 ;
; 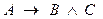 ~
~  ~
~  .
.
У логіці висловлювань будь-яку її формулу можна поставити у відповідність деякому складному висловлюванню природної форми і навпаки. Для того щоб перетворити складне речення у формулу логіки висловлювань, необхідно виконати такі кроки алгоритму.
1. Шляхом аналізу складного речення визначити, є воно скороченим чи ні.
2. Якщо речення скорочене, то його потрібно замінити повним варіантом.
3. У повному варіанті виділити прості речення й взяти їх у дужки, залишивши поза дужками службові слова.
4. Процес взяття у дужки повторювати доти, поки повністю все складне речення не виявиться взятим у дужки.
5. Замінити сполучники та звороти природної мови відповідними логічними зв’язками, а прості речення – атомарними формулами.
Приклад 1.3.6. Речення “ Оскільки я ліг пізно спати, я проспав і через це не пішов на роботу ” записати у вигляді формули логіки висловлювань.
Розв’язання. У цьому складному реченні виділимо прості речення та візьмемо їх у дужки – “ Оскільки (я ліг пізно спати), (я проспав) і через це не (пішов на роботу) ”.
Усі три прості речення зв’язані службовими словами, що виражають логічні відношення, а перед третім реченням стоїть частка “ не ”, що відповідає логічній операції
“ заперечення ”. Оскільки третє речення не є повним, то доповнюємо його відсутнім підметом “ я ” і введемо атоми:
A – “ Я ліг пізно спати ”, B – “ Я проспав ”, C – “ Я пішов на роботу ”.
Замінивши прості речення символами атомів, а службові слова – логічними зв’язками, отримаємо формулу логіки висловлювань  Ø
Ø  .
.






