Приписування значень I або X атомарним формулам, що входять до складних формул, називають інтерпретацією.
Усі формули логіки висловлювань розділяються на тотожно істинні, тотожно хибні та нейтральні.
Означення 1.4.1. Формулу називають тотожно істинною (тавтологією, або загальнозначущою ), якщо вона набуде значення “ Істина ” на всіх інтерпретаціях (наборах значень змінних).
Наприклад, висловлювання “ Він піде чи не піде в крамницю ” є тавтологією, оскільки або перше висловлювання, або друге обов’язково відбудеться.
Приклад 1.4.1. За допомогою таблиці істинності визначити істинність значення формули логіки висловлювання
.
Розв’язання. Будуємо таблицю істинності для заданої формули логіки висловлювання (табл. 1.4.1).
Таблиця 1.4.1
| 
| 
| 
| 
|
| X | X | I | X | I |
| X | I | I | X | I |
| I | X | X | X | I |
| I | I | I | I | I |
Із таблиці істинності випливає, що задане висловлювання “ Істинне ” на всіх чотирьох можливих наборах змінних цього висловлювання, тому воно є тавтологією.
Приклад 1.4.2. Довести, якщо висловлювання і 
тавтології, то теж тавтологія.
Розв’язання. За умовою висловлювання і – тавтології. Нехай при деякому розподілі значень істинності для пропозиційних змінних, які входять в і , набуває значення “ Хибність ”. Але оскільки є тавтологія, то при тому самому розподілі значень істинності набуває значення “ Істинно ”. Тоді висловлювання набуває значення “ Хибність ”, але це є суперечністю, тому що є тавтологією.
Означення 1.4.2. Формулу називають тотожно хибною (суперечною,або нездійсненною ), якщо вона набуває значення “ Хибність ” на всіх інтерпретаціях (наборах значень змінних).
Наприклад, висловлювання “ Вона рухається в напрямку до школи і вона не рухається в напрямку до школи ” є суперечливими, оскільки неможливо одночасно робити і те й інше. Тобто це висловлювання є тотожно хибним.
Приклад 1.4.3. За допомогою таблиці істинності визначити, чи є тотожно хибною формула 
.
Розв’язання. Будуємо таблицю істинності для заданої формули логічного висловлювання (табл. 1.4.2).
Таблиця 1.4.2
|
|
|
|
|
|  
|
| X | X | I | I | I | X | X |
| X | I | I | I | X | I | X |
| I | X | X | X | I | I | X |
| I | I | I | X | X | I | X |
Із таблиці істинності випливає, що висловлювання, задане формулою, набуває значення “ Хибність ” на всіх чотирьох можливих наборах змінних цього висловлювання, тобто є тотожно хибним.
Означення 1.4.3. Формулу називають нейтральною (не загальнозначущою, або несуперечливою ), якщо вона на одних інтерпретаціях набуває значення “ Істина ”, а на інших “ Хибність ”.
Приклад 1.4.4. За допомогою таблиці істинності визначити, чи є нейтральною формула 
.
Розв’язання. Будуємо таблицю істинності за заданою формулою логічного висловлювання (табл. 1.4.3).
Таблиця 1.4.3
|
|
|
| 
| 
|
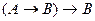
| X | X | I | X | I |
| X | I | I | I | I |
| I | X | X | I | X |
| I | I | I | I | I |
Із таблиці істинності випливає, що висловлювання, задане логічною формулою, набуває на різних інтерпретаціях два значення “ Істина ” чи “ Хибність ”. Тому формула логічного висловлювання є нейтральною.
Особлива роль в алгебрі висловлень належить тотожно істинним формулам як способам правильних умовиводів, що від істинних посилань приводять до істинних висновків. Для доведення, що наведені формули є тавтологіями, достатньо застосувати таблиці істинності.
Наведемо приклади таких формул:
Означення 1.4.4. Міркування називають правильним, якщо воно виражається тотожно істинною формулою.
Для перевірки правильності міркування будують відповідно до нього формулу і визначають, чи є вона тотожно істинною. Істинність формули можна перевірити або за допомогою таблиці істинності, де на всіх інтерпретаціях вона набуває значення “ Істина ”, або за допомогою тотожних перетворень, звівши їх до вигляду одного із логічних законів, де одержують теж значення “ Істина ”, що відповідно до формули міркування є тавтологією.
Означення 1.4.5. Формули алгебри висловлень α(А1, А2,…,Аn) i β(А1, А2,…,Аn) називаються рівносильними (логічно еквівалентними), якщо значення істинності формули α збігається зі значенням істинності формули β.
