Составляют схематический чертеж согласно заданному варианту. Уравнивание углов выполняется в следующем порядке.
4.3.1. Выбирают узловую линию, т.е. линию, примыкающую к узловой точке 5. При выборе в качестве узловой линии 4-5 (что рекомендуется сделать), решаемая система разделится на три одиночных теодолитных хода, которые опираются на исходные пункты.
4.3.2. Для каждого хода по координатам исходных пунктов решают обратные геодезические задачи и находят исходные дирекционные углы. Со схемы ходов выписывают в ведомость координат измеренные углы и исходные дирекционные углы по трем одиночным ходам. Подсчитывают суммы измеренных углов по каждому ходу.
4.3.3. Находят значения дирекционных углов узловой линии по каждому ходу по формулам:
, или 
(4.1)
где 
;
– число углов, входящих в сумму 
и 
;
– сумма углов правых по ходу;
– сумма углов левых по ходу.
Результаты вычислений выписывают в графу 2 табл. 4.1. Попутно в графу 3 записывают число углов n по каждому ходу.
Таблица 4.1
Вычисление окончательного значения дирекционного угла узловой линии 
| № хода | 
| 
| 
| 
| 
| 
| 
| 
|
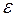
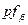
4.3.4. Прежде чем приступить к нахождению средневесового значения дирекционного угла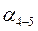 
узловой линии необходимо проверить качество угловых измерений в теодолитных ходах. Для этого составляют разности вычисленных дирекционных углов и получают невязки. Первую разность составляют из дирекционных углов по двум ходам с наименьшим числом углов. Другую разность составляют из дирекционных углов, вычисленных по третьему ходу и одному из двух первых по формулам:
(4.2)
Невязки сравнивают с допустимыми значениями невязок, которые находят по формуле
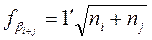, (4.3)
где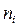 
и 
- количество углов в i -ом и j -ом ходах.
При допустимости невязок, производят уравнивание дирекционных углов.
Определяют веса вычисленных значений дирекционных углов узловой линии по формуле
, (4.4)
где 
– произвольный коэффициент, выбираемый так, чтобы веса выражались числами, близкими к единице. Веса записывают в графу 4 табл. 4.1 с округлением до 0,01.
Вычисляют средневесовое значение дирекционного угла узловой линии
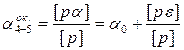, (4.5)
где 
– остатки, вычисляемые по формуле
(i = 1, 2, 3). (4.6)
После этого определяют угловые невязки по всем трем ходам по значениям дирекционного угла узловой линии для правых углов по ходу
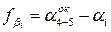(i = 1, 2, 3), (4.7)
а для левых углов по ходу
(i = 1, 2, 3). (4.8)
Контроль правильности вычисления дирекционного угла 
и невязок 
проверяют по формулам
, или 
.
За счет округления величины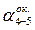 
появляется ошибка округления 
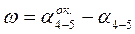. Для определения 
следует при делении 
в результате удерживать две дополнительные цифры.
В этом случае контролем является выражение
[ Pf ] 
.
Если в ходе имеются и правые и левые углы, то надо изменить знак произведений Pf в столбце 8 табл. 4.1 на противоположный, чтобы все произведения соответствовали только правым или только левым углам.
4.3.5. СКП измерения угла вычисляют по формуле
, (4.9)
где 
– СКП, вычисляемая по формуле
, (4.10)
где N – количество ходов.
4.3.6. Полученное окончательное значение дирекционного угла узловой линии принимают за исходное и записывают в графу "Дирекционные углы" ведомости вычисления координат.
Вычисляют теоретические суммы углов по каждому ходу, которые записывают в графу 2 ведомости вычисления координат. После этого вновь вычисляют невязки и сличают их с полученными в графе 7 табл. 4.1.
Полученные невязки распределяют с противоположным знаком поровну на углы соответствующих ходов (с округлением до 0,1´).
Для проверки правильности распределения невязок подсчитывают суммы исправленных углов. Они должны быть равны теоретическим суммам по каждому ходу.
По исправленным углам вычисляют дирекционные углы всех линий.
После этого переходят к уравниванию приращений координат.
4.3.7. Со схемы ходов выписывают в ведомость координат горизонтальные проложения сторон теодолитных ходов и координаты начальных исходных пунктов. Вычисляют приращения координат и их суммы по каждому ходу, а затем – координаты узловой точки по всем трем ходам по формулам
; 
(i = 1, 2, 3). (4.11)
Результаты вычислений записывают в табл. 4.2. по вычислению окончательных значений координат узловой точки 5.
Таблица 4.2
