Свойства зубчатого механизма во многом определяются выбором типа кривых, по которым очерчиваются боковые поверхности зубьев и которые определяют профиль зубьев зубчатых колес. Выбор же кривых для любых зубчатых колес должен, прежде всего, удовлетворять основной теореме зацепления и ее следствиям.
Основная теорема зацепления.
Общая нормаль к соприкасающимся профилям зубьев в данный момент зацепления делит линию центров колес на части, обратно пропорциональные угловым скоростям.
Для доказательства основной теоремы рассмотрим зацепление двух зубьев в некоторый момент времени (рис. 38) в точке М (М 1 и М 2) со скоростями этих точек VM 1 = R 1 
и VM 2 = – R 2 
соответственно.
Рис. 38. К доказательству основной теоремы зацепления
Пусть NN – общая нормаль в данный момент в точке М. Очевидно, что условием непрерывности зацепления при вращении колес будет равенство проекций скоростей VM 1 и VM 2на общую нормаль, т. е. 
. В противном случае (при 
) получим либо отставание одного зуба от другого (
), либо «внедрение» (
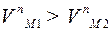) – что недопустимо.
Обозначая углы векторов с нормалью через 
и 
, имеем:
.
Из подобия 
и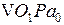 
:
,
что и требовалось доказать.
Следствие 1. Проекции скоростей на общую касательную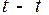 
не равны между собой. Поэтому зацепление зубьев происходит со скольжением профилей, от которого возникает износ и потери на трение, зависящие от скорости скольжения 
.
Скольжения не будет только тогда, когда 
, т. е. в момент зацепления зубьев на линии центров.
Следствие 2. Для постоянства передаточного отношения необходимо, чтобы общая нормаль NN в любой момент зацепления проходила через одну и ту же точку на линии центров, называемую полюсом зацепления Р.
Окружности, проходящие через полюс зацепления, называют начальными (rω 1 и rω 2). Они являются центроидами относительного движения колес. Расстояние по дуге начальной окружности между двумя соседними зубьями называется шагом по начальной окружности (Pω 1 и Pω 2). Так как начальные окружности – центроиды, то Pω 1 = Pω 2 = Pω.
Числа зубьев колес обычно обозначаются через z (z 1и z 2). Тогда следующие равенства очевидны: 
и 
.
Из основной теоремы зацепления для круглых колес имеем:
, (6.1)
т. е. передаточное отношение пары зубчатых колес с неподвижными осями обратно пропорционально числу зубьев, взятому с соответствующим знаком. Для внешнего зацепления – знак «минус», для внутреннего – «плюс».
Из выражения (6.1) следует:
. (6.2)
Условиям основной теоремы зацепления и ее следствиям соответствует большое число кривых. Можно даже взять произвольный профиль одного зуба и получить, пользуясь основной теоремой, профиль зуба сопряженного с ним колеса. Однако такой профиль не будет соответствовать нижеперечисленным требованиям, предъявляемым к зубчатым колесам:
- профили должны быть взаимно просты и технологичны в производстве;
- зубчатые колеса должны быть взаимозаменяемы;
- профили зубьев должны иметь минимальный износ поверхностей и достаточную прочность и долговечность;
- профили должны давать постоянное давление на опоры для обеспечения долговечности подшипников.
В настоящее время в машиностроении и приборостроении основной кривой для профилей зубьев является эвольвента круга, предложенная Л. Эйлером в 1754 г. Более чем двухсотлетнее применение эвольвентных зубчатых колес свидетельствует об удачном выборе кривой, особенно в связи с изобретением прогрессивного метода обработки (метода обкатки).
