Характеристика сил, действующих на звенья механизма

Силы и моменты пар сил, приложенные к механизму, можно разделить на следующие группы:

- движущие силы и моменты сил, совершающие положительную работу;

- силы и моменты сил сопротивления, совершающие отрицательную работу;

- силы тяжести;

- силы взаимодействия между звеньями, т. е. реакции в кинематических парах.

Движущие силы и моменты сил, совершающие положительную работу, приложены к ведущим звеньям.

Силы и моменты сил сопротивления, совершающие отрицательную работу, делятся на силы полезного сопротивления, которые приложены к ведомым звеньям, и силы вредного сопротивления со стороны среды, в которой движутся звенья (последними в силовом анализе пренебрегают).

Силы тяжести на отдельных участках движения могут совершать как положительную, так и отрицательную работу. Однако за цикл движения (полный оборот ведущего звена) работа этих сил равна нулю, т. к. центры масс движутся по замкнутым траекториям.

Силы взаимодействия между звеньями, т. е. реакции в кинематических парах, согласно третьему закону Ньютона, равны и противоположны по направлению.

Нормальные составляющие сил реакций работы не совершают, а касательные составляющие – это силы трения, и они совершают отрицательную работу. При силовом анализе трением пренебрегают.

Силы и моменты пар сил первых трех групп относятся к категории внешних сил. Силы 4-й группы являются внутренними,если рассматривать весь механизм в целом. Если же рассматривать отдельные звенья, то реакции в кинематических парах со стороны отброшенных звеньев считаются внешними силами и входят в уравнения равновесия.

При силовом расчете механизмов, в зависимости от задачи и желаемой точности решения ее, могут быть приняты во внимание те или иные действующие силы (силы тяжести, силы трения, силы инерции и т. д.)

Так, например, в тихоходных механизмах силы инерции, возникающие в результате движения, незначительны по сравнению с внешними силами, поэтому ими в большинстве случаев можно пренебречь, а силы трения необходимо учитывать.

В быстроходных механизмах силами инерции пренебречь нельзя, т. к. они могут иметь величину того же порядка, а в некоторых случаях даже большую, чем внешние силы.

Силовой расчет с учетом сил инерции называется кинетостатическим методом расчета.

Кинетостатический метод

Сущность кинетостатического метода сводится к условной замене на основании принципа Даламбера задачи динамики задачей статики.

В применении к механизмам сущность кинетостатического метода может быть сформулированного следующим образом.

Если ко всем внешним силам, действующим на звено механизма, условно приложить силы инерции, то под действием всех этих сил звено может рассматриваться в равновесии.

При решении задачи кинетостатического расчета должны быть заданы:

- закон движения ведущего звена;

- размеры звеньев;

- массы звеньев механизмов;

- моменты инерции звеньев.

Задача сводится к определению реакций в кинематических парах и значения уравновешивающего момента (силы).

Эти величины необходимы для расчета деталей на прочность, определение мощности двигателя, износа трущихся частей и т. д.

Определение сил инерции

Как известно из теоретической механики, элементарные силы инерции можно привести к главному вектору и главному моменту :

, (4.1)

где m – масса звена;

a _S – ускорение центра масс;

– угловое ускорение звена;

– момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения (сокращенно – осевой момент инерции).

Знак «минус» в формулах означает, что сила инерции направлена против ускорения (момент сил – против углового ускорения).

Следует отметить, что главный вектор и главный момент сил инерции не имеют физического содержания, и в действительности к звену эти силы не приложены. Они входят в уравнения кинетостатики как чисто математические величины, посредством которых учитывается влияние ускоренного движения звеньев, и условно относятся к разряду внешних сил.

В частных случаях плоское движение может быть вращательным или поступательным, при этом возникает только момент сил инерции (вращение звена с ускорением) или же только сила инерции (поступательное неравно­мерное движение).

С учётом сил инерции уравнения кинетостатики для каждого звена имеют вид:

, (4.2)

где , 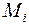– внешние силы и моменты пар сил, приложенные к i -му звену.

Изучение сил инерции, развивающихся при движении звеньев механизма, осуществляется в зависимости от характера движения рассматриваемого звена.

 

Рассмотрим определение сил инерции при поступательном движении (рис. 18).

Рис. 18.К определению сил инерции при поступательном движении

 

 

Дано: m; ; = 0.

Решение:

Вывод: При определении сил инерции звена, совершающего поступательное движение, учитывается только сила инерции с модулем, равным произведению массы на ускорение центра тяжести. Направление силы инерции противоположно ускорению, точка приложения – центр тяжести звена.

 

Рассмотрим определение сил инерции при вращательном движении.

1. Вращательное движение с постоянной угловой скоростью уравновешенного звена; центр тяжести совпадает с центром вращения (рис. 19).

Рис. 19. К определению сил инерции при вращательном движении
с постоянной угловой скоростью

 

 

Дано: m; ; = 0; aS = 0.

Решение:

Вывод: Инерционности нет.

2. Вращательное движение с переменной угловой скоростью уравновешенного звена; центр тяжести совпадает с центром вращения (рис. 20).

Рис. 20.К определению сил инерции при вращательном движении
спеременной угловой скоростью

Дано: m; ; ; aS = 0.

Решение:

Вывод: В этом случае действует только момент от сил инерции.

 

3. Вращательное движение с переменной угловой скоростью неуравновешенного звена; центр тяжести не совпадает с центром вращения (рис. 21).

Рис. 21. К определению сил инерции при вращательном движении
спеременной угловой скоростьюнеуравновешенного звена

Дано: m; J_S = mρ ²; a_S; h – плечо силы; 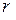– радиус инерции.

K – центр качания физического маятника, расстояние до которого от центра вращения A определяется по формуле:

. (4.3)

Решение:

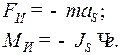
Сумма моментов от сил инерции, действующих на звено, равна

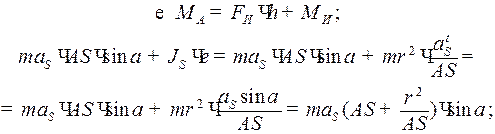
. (4.4)

Вывод: Согласно формуле (4.4) инерционность звена в данном случае учитывается только силой инерции с точкой приложения в точке K.

Положение центра качения маятника нередко имеет существенное значение в процессе проектирования многих машин. Можно использовать возникающую силу инерции для совершения полезной работы и тем самым уменьшить давление на шарниры.

 

Рассмотрим определение сил инерции при сложном движении.

1. Метод приведения к одной силе (рис. 22а).

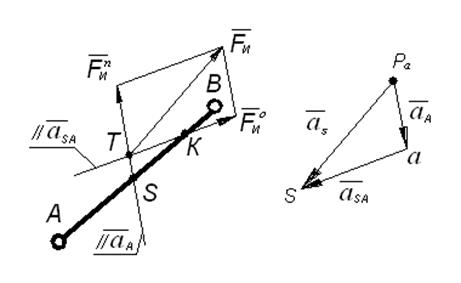
Рис. 22а.К методу приведения к одной силе

Дано: m; J_S и план ускорений.

Решение: Звено AB совершает сложное движение, которое можно представить как состоящее из двух элементарных движений:

- переносного поступательного движения вместе с полюсом A;

- относительного вращения звена вокруг полюса A:

;

;

.

Вывод: В случае сложного движения звена инерционность звена можно представить в виде одной силы инерции , абсолютная величина которой равна ma_S (произведению массы на ускорение центра тяжести) и направление противоположно . Точка приложения – точка Т, положение которой определяется следующим образом:

1) через центр тяжести S проводим линию параллельно ускорению точки, принятой за полюс (точка A) – ;

2) находим положение центра качания физического маятника К по формуле (4.3);

3) через К проводим линию параллельно вектору ускорения центра тяжести относительно полюса – ;

4) пересечение этих линий определяет положение точки Т.

 

2. Метод приведения к силе и моменту (рис. 22б).

Рис. 22б.К методу приведения к силе и моменту

 

 

Силы инерции звена можно привести к одной силе инерции , приложенной в центре тяжести звена и моменту инерции звена относительно центра тяжести :

4.5. Условие статической определимости
кинематической цепи

Плоская кинематическая цепь может состоять из кинематических пар
5-го класса (вращательных, поступательных) и пар 4-го класса (высших, у которых звенья соприкасаются в точке).

Как известно из теоретической механики, сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности. В поступательной паре (рис. 23, а) реакции направлены перпендикулярно направляющей. Неизвестных здесь две: величина силы F_O1 и точка ее приложения (расстояние h).

 

а) б) в)

Рис. 23. К определению условия статической определимости
кинематической цепи

 

 

Во вращательной паре равнодействующая сил реакции направлена по нормали к цилиндрической поверхности, т. е. проходит через центр шарнира (рис. 41, б). Неизвестными являются: направление реакции (угол ) и величина силы. Таким образом, эта пара также вносит в уравнения кинетостатики две неизвестных.

Следовательно, от каждой силы, действующей в любой низшей кинематиче­ской паре, в расчетных уравнениях (4.2) появляются две неизвестные величины.

В высших парах сила взаимодействия между звеньями направлена по общей нормали и приложена в точке касания, т. е. известны и направление, и точка приложения силы (рис. 41, в), неизвестна лишь ее величина. Поэтому в расчетных уравнениях члены, образованные силами взаимодействия в высших парах, содержат по одному неизвестному.

В общем случае плоская кинематическая цепь содержит p ₅ пар 5-го класса (низших) и p ₄ пар 4-го класса (высших), поэтому общее число неизвестных равно:

N_H = 2 p ₅+ p ₄. (4.5)

Число уравнений статики для каждого звена плоского механизма равно трем, значит, общее число уравнений для n подвижных звеньев:

N_У = 3 n. (4.6)

Чтобы система была статически определимой, число уравнений (N_У) должно быть равно числу неизвестных (N_H). Приравниваем (4.5) и (4.6), после чего получим:

3 n = 2 p ₅ + p ₄, или 3 n – 2 p ₅– p ₄= 0. (4.7)

Если заменить высшие пары низшими, то 3 n – 2 p ₅= 0.

Из этого можно сделать вывод, что группы Ассура являются статически определимыми.

Из выражения (4.7) определяем соотношение между числом звеньев и числом кинематических пар 5-го класса: n = 2/3 p ₅.

На основании вышеизложенного формулируется общая методика силового анализа: расчет следует проводить по структурным группам, начиная с наиболее удаленной от начального звена и заканчивая начальным звеном (механизмом I класса). Таким образом, силовой расчет проводится в порядке, обратном кинематическому.