5.3.1. Трение в поступательной паре
Как было отмечено ранее, трение скольжения возникает в низших кинематических парах. В плоских механизмах это пары 5-го класса, т. е. поступательная, вращательная и винтовая.
Рассмотрим действие сил с учетом трения на примерах типовых механизмов.
Имеется кривошипно-ползунный механизм (рис. 31), к входному звену которого приложен момент движущих сил  =
=  .
.

Рис. 31. Соотношение сил в поступательной паре
К выходному звену приложена результирующая сила  от сил полезного сопротивления, силы тяжести, силы инерции. Необходимо определить силу трения, которая также является силой сопротивления.
от сил полезного сопротивления, силы тяжести, силы инерции. Необходимо определить силу трения, которая также является силой сопротивления.
Силами тяжести и инерции шатуна пренебрегаем. Если ползун прижимается кодной из сторон направляющих, то сила трения определяется согласно закону Кулона:
 , (5.8)
, (5.8)
где  – нормальная реакция направляющей.
– нормальная реакция направляющей.
Затем можно определить реакцию  или необходимую движущую силу уже известными методами, описанными в разделе 4.6.
или необходимую движущую силу уже известными методами, описанными в разделе 4.6.
5.3.2. Трение во вращательной паре
Рассмотрим вращение вала 1 во втулке 2 подшипника (рис. 32).
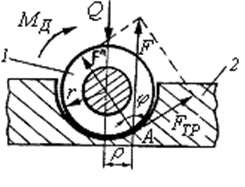
Рис. 32. Соотношение сил во вращательной паре
При наличии зазора вал как бы набегает на втулку (или вкладыш) подшипника, поэтому звенья соприкасаются в точке А. Реакция  параллельна силе
параллельна силе  , приложенной к валу. В результате трения полная реакция должна быть отклонена от нормальной составляющей на угол трения
, приложенной к валу. В результате трения полная реакция должна быть отклонена от нормальной составляющей на угол трения 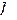 . Величина силы трения (рис. 32):
. Величина силы трения (рис. 32):
 . (5.9)
. (5.9)
Момент движущих сил 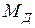 , приложенный к валу, уравновешивается моментом сил сопротивления
, приложенный к валу, уравновешивается моментом сил сопротивления  :
:
 , (5.10)
, (5.10)
где r – радиус цапфы вала.
Учитывая, что f cos 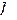 = tg
= tg 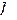 cos
cos 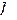 = sin
= sin 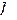 , преобразуем выражение (5.10):
, преобразуем выражение (5.10):
MC = Qr sin 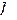 = Q
= Q  , (5.11)
, (5.11)
где  – радиус круга трения,
– радиус круга трения,  = r sin
= r sin 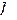 (рис. 32).
(рис. 32).
Если описать из центра вала окружность радиусом  , то она будет касательной по отношению к
, то она будет касательной по отношению к  .
.
Для малых углов sin 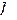
 tg
tg 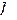 , поэтому приближенно момент сил трения вычисляют по формуле:
, поэтому приближенно момент сил трения вычисляют по формуле:
 , (5.12)
, (5.12)
где  – для неприработавшихся цапф;
– для неприработавшихся цапф;
 – для приработавшихся цапф.
– для приработавшихся цапф.
Здесь  – коэффициент трения скольжения для плоской поверхности.
– коэффициент трения скольжения для плоской поверхности.
5.3.3. Трение в винтовой паре
При рассмотрении трения в винтовой паре принимают следующие допущения:
- сила взаимодействия винта и гайки приложена на среднем диаметре резьбы;
- пространственную пару сводят к плоской, т. е. развертывают винтовую линию на плоскость и рассматривают равновесие ползуна на наклонной плоскости (рис. 33, а).
а)  б)
б) 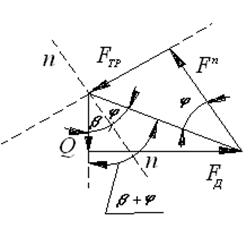
Рис. 33. Соотношение сил в винтовой паре
На ползун действуют силы: движущая ( ), осевая (
), осевая ( ), нормальная реакция (
), нормальная реакция ( ) и сила трения (
) и сила трения (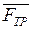 ). Уравнение равновесия имеет вид:
). Уравнение равновесия имеет вид:
 . (5.13)
. (5.13)
Строим план сил, из которого определяем  (рис. 51, б)
(рис. 51, б)
 . (5.14)
. (5.14)
После этого можно определить момент внешних сил, приложенных к гайке при движении ее вверх по резьбе, т. е. при завинчивании:
 , (5.15)
, (5.15)
где 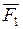 – сила, приложенная к гайке;
– сила, приложенная к гайке;
r1 – радиус вписанной окружности гайки;
r – средний радиус резьбы.
Если ползун будет двигаться по винтовой линии вниз, то сила 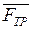 будет направлена в противоположную сторону и реакция
будет направлена в противоположную сторону и реакция  отклонится от нормали на угол
отклонится от нормали на угол 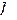 . Уравнение (5.15) примет вид:
. Уравнение (5.15) примет вид:
 . (5.16)
. (5.16)
При  момент становится отрицательным, т. е. движение вниз по резьбе невозможно. Такой винт называют самотормозящимся, широкое применение он нашел в домкратах.
момент становится отрицательным, т. е. движение вниз по резьбе невозможно. Такой винт называют самотормозящимся, широкое применение он нашел в домкратах.
Трение качения
Трение качения возникает в высших кинематических парах, например, при относительном движении профилей зубьев колес, ролика по кулачку и т.д. Для определения условия перекатывания одного звена по другому рассмотрим цилиндр, лежащий на плоскости (рис. 34).
а) 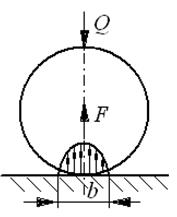 б)
б) 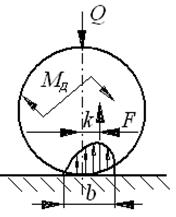 в)
в) 
Рис. 34. К определению трения качения
Под действием силы  цилиндр в зоне контакта с плоскостью будет упруго деформироваться (рис. 34, а). Равнодействующая напряжений
цилиндр в зоне контакта с плоскостью будет упруго деформироваться (рис. 34, а). Равнодействующая напряжений  =
=  .
.
Если приложить к цилиндру пару сил, момент которой равен 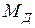 , чтобы цилиндр катился с постоянной скоростью, то сопротивление движению перекатывания определяется этим моментом. При этом эпюра напряжений смятия будет несимметричной, вследствие упругого гистерезиса, и равнодействующая напряжений будет смещена в сторону движения на величину k (рис. 34, б). Из условия равномерного движения
, чтобы цилиндр катился с постоянной скоростью, то сопротивление движению перекатывания определяется этим моментом. При этом эпюра напряжений смятия будет несимметричной, вследствие упругого гистерезиса, и равнодействующая напряжений будет смещена в сторону движения на величину k (рис. 34, б). Из условия равномерного движения
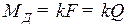 . (5. 17)
. (5. 17)
Если заменить момент парой сил на плече r, то получим:
 , (5.18)
, (5.18)
где k – коэффициент трения качения, определяющий сопротивление перекатыванию.
Из чертежа (рис. 34, б) видно, что k – это плечо реакции F, поэтому коэффициент трения качения имеет размерность длины.
Из выражения (5.18) определим движущую силу:
 . (5.19)
. (5.19)
Качение цилиндра будет происходить при условии, что  (рис. 34, в), в противном случае цилиндр будет скользить.
(рис. 34, в), в противном случае цилиндр будет скользить.
Учитывая, что трение скольжения 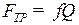 и принимая во внимание зависимость (5.19), выразим условие отсутствия скольжения:
и принимая во внимание зависимость (5.19), выразим условие отсутствия скольжения:
 , (5.20)
, (5.20)
где f – коэффициент трения скольжения; r – радиус тела качения (цилиндра).




