При проектировании новых машин и механизмов составляют несколько вариантов кинематических схем, проводят структурный анализ и выбирают лучший вариант. Затем осуществляется кинематический анализ.
Кинематическийанализ – это изучение движения механизма без учета действующих сил. Движения механизма описываются с помощью кинематических характеристик.
Под кинематическимихарактеристиками (параметрами) понимают перемещения, скорости и ускорения точек звеньев, а также угловые скорости и ускорения звеньев.
В результате кинематического анализа устанавливают соответствие кинематических параметров (перемещений, траекторий точек, скоростей и ускорений звеньев) заданным условиям, например: определение траекторий точек необходимо, чтобы при проектировании корпуса машины исключить столкновение звеньев при их движении. Кроме того, в результате кинематического анализа получают исходные данные для выполнения динамических расчётов. Знание кинематических параметров необходимо для расчёта сил инерции и моментов сил инерции, кинетической энергии механизма и мощности.
Кинематическое исследование схем механизмов выполняют графическими и аналитическими методами. Первые отличаются наглядностью и относительной простотой, но не дают точных результатов. Аналитический метод позволяет получить требуемую точность, но отличается большей сложностью и трудоемкостью вычислений.
Перемещения, скорости и ускорения звеньев определяют для нескольких положений в пределах цикла работы механизма, т. е. за один оборот ведущего звена.
Основными методами кинематического анализа являются:
- графический метод (метод построения планов);
- аналитический метод;
- метод построения кинематических диаграмм.
Используя принципы структурного анализа, т. е. разложения механизма на группы Ассура, можно применять методы кинематического анализа не ко всему механизму в целом, а к отдельным его частям, что, как правило, упрощает задачу.
Задачи кинематического анализа
К основным задачам кинематического анализа относятся:
- определение положений звеньев при заданном положении ведущего звена и построение траекторий отдельных точек;
- установление зависимости перемещений отдельных звеньев от законов перемещения ведущего звена;
- определение зависимости скоростей отдельных звеньев от закона движения ведущего звена;
- установление зависимости ускорений отдельных звеньев от закона движения ведущего звена.
Движение звеньев зависит от закона движения ведущего звена, поэтому при решении задач кинематического анализа должны быть заданы следующие данные:
- структурная схема механизма с указанием размеров звеньев и параметров их расположения;
- закон движения ведущего звена.
При кинематическом исследовании механизма расчет и построение планов скоростей и ускорений начинают от ведущего звена, угловая скорость которого обычно постоянна, и далее – по группам Ассура в порядке их присоединения.
Планы положений механизма
Изображение кинематической схемы механизма, соответствующее определенному положению начального звена, называется планом механизма.
Планы строятся в заданном масштабе. При этом различают понятия «масштаб» и «масштабный коэффициент».
Масштабомфизическойвеличины называют длину отрезка в миллиметрах, изображающую единицу измерения этой величины.
Масштабнымкоэффициентомфизическойвеличины называют отношение численного значения физической величины к длине отрезка в миллиметрах, изображающего эту величину.
Масштаб и масштабный коэффициент являются взаимно обратными величинами. Масштабные коэффициенты обозначают буквой 
с индексом, указывающим, к какой величине они относятся.
Например, масштабный коэффициент длин 
для плана механизма есть отношение какой-либо длины 
в метрах к отрезку АВ, изображающему эту длину на чертеже в миллиметрах: 
= 
/ АВ.
Рассмотрим построение планов механизма на примере.
Пример 1. Кривошипно-ползунный механизм (рис. 16).
Выбираем крайнее положение кривошипа (кривошип и шатун располагаются на одной линии).
Рис. 16. Построение плана положений кривошипно-ползунного механизма
Делим окружность радиуса ОА на равные части. Из точек деления (А 1, А 2, …)делаем засечки на оси движения ползуна (В 1, В 2 ...) радиусом, равным длине шатуна. Соединяем одноименные точки (А 1и В 1, А 2 и В 2...).
Найденные положения точки Вопределяют положение поршня (ползуна) при рабочем ходе – В 1, В 2, В 3; при холостом ходе – В 4, В 5.
Построение планов скоростей и ускорений
Построение планов скоростей и ускорений рассмотрим на примере кривошипно-ползунного механизма (рис. 17).
Порядок построения, обозначения, формулы аналогичны рассмотренным ранее, поэтому этот и последующие разделы даны в конспективной форме, без подробных текстовых объяснений.
а) б) в)
Рис. 17. Пример построения плана скоростей и ускорений
структурной группы 2-го вида:
а) план механизма; б) план скоростей; в) план ускорений
Пример.
Дано: кинематическая схема механизма; угловая скорость кривошип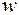а 
ОА.
Определить: скорость и ускорение точки В; угловую скорость и угловое ускорение звена АВ.
Механизм образован присоединением к ведущему звену группы Ассура II класса 2-го вида. Выделим эту группу и построим для нее план скоростей (рис. 17, б). Скорость точки В определим с помощью уравнения:
.
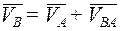Известны величина и направление скорости точки A, вычисляемой по формуле V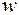A = OA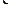 
lOA; направления скоростей 
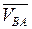и 
, где 
; 
x-x.
Отрезок paа,изображающий скорость точки А на плане, выбираем произвольным по величине.
Масштабный коэффициент 
V = VA / pVа.
Через точку А проводим направление относительной скорости 
; через полюс (неподвижную точку) проводим направление абсолютной скорости точки В – горизонтальную прямую, параллельную x-x. Определяем скорость точки В
VB= pVb 
V.
Угловая скорость звена АВ
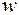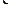
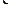
AB = VBA / lAB = ab V / АВ l.
Вектор относительной скорости вращает звено против часовой стрелки (рис. 17).
План ускорений строим по уравнению:
где 
.
На плане ускорений, построенном с учетом масштабного коэффициента 
, правая часть уравнения изображена соответствующими векторами: 
, 
, 
.
Результирующий вектор 
изображает абсолютное ускорение точки В
.
Угловое ускорение звена АВ находим по касательной составляющей 
:
Направление углового ускорения находим, перенося вектор касательной составляющей относительного ускорения в точку В механизма (рис. 17, в, а).
Свойства плана скоростей
На основании рассмотренных построений можно определить следующие свойства плана скоростей:
- на плане скоростей лучи, выходящие из полюса, изображают абсолютные скорости точек звена, а отрезки, соединяющие концы лучей, – относительные скорости соответствующих точек;
- неподвижные точки плана механизма на плане скоростей располагаются в полюсе;
- векторы относительных скоростей направлены на плане скоростей
к первой букве индекса. Например, 
– скорость точки С относительно В на плане скоростей читается: «отрезок bс, вектор направлен к точке с»;
- векторы относительных скоростей точек жесткого звена образуют на плане скоростей фигуру, подобную этому звену, повернутую на 90° в направлении угловой скорости звена. Этот вывод называется принципом подобия в плане скоростей и позволяет определить скорость любой точки звена графически, если известны скорости хотя бы двух точек этого звена;
- имея построенный план скоростей, всегда можно построить касательную и нормаль к траектории движения точки, не строя траекторию. Любая абсолютная скорость – касательная к траектории движения;
- имея построенный план скоростей, можно определить мгновенный центр скоростей всех звеньев механизма.
Свойства плана ускорений
На основании рассмотренных построений можно вывести следующие свойства плана ускорений:
- векторы абсолютных ускорений всегда выходят из полюса;
- отрезки, соединяющие концы векторов абсолютных ускорений на плане ускорений, изображают полные относительные ускорения. Направление относительного ускорения к той букве плана ускорений, которая стоит первая в его обозначении;
- полные нормальные ускорения всегда выходят от полюса и направлены к центру вращения звена;
- неподвижные точки механизма на плане ускорений находятся в полюсе;
- векторы относительных ускорений точек жесткого звена образуют на плане ускорений фигуру, подобную этому звену и повернутую относительно его на угол (180° –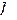 
) в направлении углового ускорения. Этим определяется принцип подобия в плане ускорений;
- зная относительные ускорения хотя бы двух точек звена, можно определить ускорение любой точки этого звена, пользуясь принципом подобия;
- имея построенный план ускорений можно определить мгновенный центр ускорений (МЦУ).
