нормаль
N
j N0
касательная плоскость
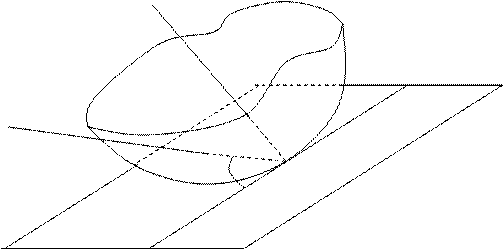
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущей NN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
.
Уравнение нормали к поверхности в этой точке:
Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Dх, у0+Dу).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности
в точке М(1, 1, 1).
Уравнение касательной плоскости:
Уравнение нормали:
Приближенные вычисления с помощью полного дифференциала
Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:
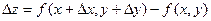
Если подставить в эту формулу выражение
то получим приближенную формулу:
Пример. Вычислить приближенно значение 
, исходя из значения функции 
при x = 1, y = 2, z = 1.
Из заданного выражения определим Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = -0,01,
Dz = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) = 
Находим частные производные:
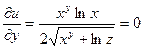
Полный дифференциал функции u равен:
Точное значение этого выражения: 1,049275225687319176.
Частные производные высших порядков
Если функция f(x, y) определена в некоторой области D, то ее частные производные 
и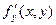 
тоже будут определены в той же области или ее части.
Будем называть эти производные частными производными первого порядка.
Производные этих функций будут частными производными второго порядка.
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
Определение. Частные производные вида и т.д. называются смешанными производными.
