Свойства операции умножения матриц

Линейная алгебра

Основные определения

Определение. Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца.

А =

 

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij ± b_ij

С = А + В = В + А.

 

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

 

a (А+В) =aА ± aВ

А(a±b) = aА ± bА

 

 

Пример. Даны матрицы А = ; B = , найти 2А + В.

2А = , 2А + В = .

 

Операция умножения матриц

 

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

.

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

 

Свойства операции умножения матриц

1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

А×Е = Е×А = А

Очевидно, что для любых матриц выполняются следующее свойство:

A×O = O; O×A = O,

где О – нулевая матрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение:

a(AB) = (aA)B = A(aB).

 

5) Если определено произведение АВ, то определено произведение В^ТА^Т и выполняется равенство:

(АВ)^Т = В^ТА^Т, где

индексом Т обозначается транспонированная матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.

Пример. Найти произведение матриц А = и В = .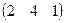

АВ = × = .

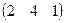ВА = 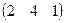× = 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.

Пример. Найти произведение матриц А= , В =

АВ = × = = .

 

Определители (детерминанты)

Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле:

det A = , где

М_1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.

Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:

det A =

Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

 

detA = , i = 1,2,…,n.

Очевидно, что различные матрицы могут иметь одинаковые определители.

Определитель единичной матрицы равен 1.

Для указанной матрицы А число М_1к называется дополнительным минором элемента матрицы a_1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Определение. Дополнительный минор произвольного элемента квадратной матрицы a_ij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.

 

Пример. Вычислить определитель матрицы А =

= -5 + 18 + 6 = 19.

 

Пример:. Даны матрицы А = , В = . Найти det (AB).

1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13;

det (AB) = det A ×det B = -26.

 

2- й способ: AB = ,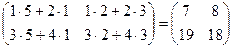

det (AB) = 7×18 - 8×19 = 126 – 152 = -26.

 

Миноры

 

Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.

Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.

Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.

 

Алгебраические дополнения

 

Определение. Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.

В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.

Теорема Лапласа. Если выбрано s строк матрицы с номерами i₁, …,i_s, то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.

 

Обратная матрица

 

Определим операцию деления матриц как операцию, обратную умножению.

Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А^-1.

Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Рассмотрим общий подход к нахождению обратной матрицы.

Исходя из определения произведения матриц, можно записать:

AX = E Þ , i=(1,n), j=(1,n),

e_ij = 0, i ¹ j,

e_ij = 1, i = j.

Таким образом, получаем систему уравнений:

,

Решив эту систему, находим элементы матрицы Х.

 

Пример. Дана матрица А = , найти А^-1.

 

 

 

Таким образом, А^-1= .

 

Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

 

,

 

где М_ji - дополнительный минор элемента а_ji матрицы А.

 

Пример. Дана матрица А = , найти А^-1.

det A = 4 - 6 = -2.

 

M₁₁=4; M₁₂= 3; M₂₁= 2; M₂₂=1

x₁₁= -2; x₁₂= 1; x₂₁= 3/2; x₂₂= -1/2

Таким образом, А^-1= .

 

Пример. Дана матрица А = , найти А³.

А² = АА = = ; A³ = = .

 

Отметим, что матрицы и являются перестановочными.

 

 

Пример. Вычислить определитель .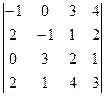

 

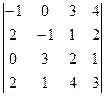= -1

 

= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.

 

= = 2(0 – 2) – 1(0 – 6) = 2.

 

= = 2(-4) – 3(-6) = -8 + 18 = 10.

Значение определителя: -10 + 6 – 40 = -44.

Базисный минор матрицы

Ранг матрицы

 

Определение. В матрице порядка m´n минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.

Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.

В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.

Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А.

 

Пример. Определить ранг матрицы.

 

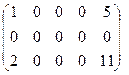~ ~ , RgA = 2.

 

Пример: Определить ранг матрицы.

 

~ ~ ~ , Rg = 2.

Пример. Определить ранг матрицы.

 

~ , Þ Rg = 2.