Закон Ома в операторной форме

Пусть имеем некоторую ветвь (см. рис. 1), выделенную из некоторой

сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.

Для мгновенных значений переменных можно записать:

.

Тогда на основании приведенных выше соотношений получим:

.

Отсюда

,

(2)

где - операторное сопротивление рассматриваемого участка цепи.

Следует обратить внимание, что операторное сопротивление соответствует комплексному сопротивлению ветви в цепи синусоидального тока при замене оператора р на . Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.

· Операторная схема замещения цепи

.

 

В качестве примера запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 - ; 2 - .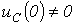

В первом случае в соответствии с законом Ома .

Тогда

и

.

Во втором случае, т.е. при 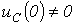, для цепи на рис. 3 следует составить операторную схему замещения, которая приведена на рис. 4. Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных токов:

откуда 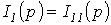; и .

 

 

· Законы Кирхгофа в операторной форме

Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю

.

Второй закон Кирхгофа: алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура

.

При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде

 

· Переходные и импульсные характеристики цепи

В основе временного метода лежит понятие переходной и импульсной характеристик цепи. Переходной характеристикой цепи называют реакцию цепи на воздействие в форме единичной функции (7.19). Обозначается переходная характеристика цепи g (t). Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (d-функции) (7.21). Обозначается импульсная характеристика h (t). Причем, g (t) и h (t)определяются при нулевых начальных условиях в цепи. В зависимости от типа реакции и типа воздействия (ток или напряжение) переходные и импульсные характеристики могут быть безразмерными величинами, либо имеют размерность А/В или В/А. Использование понятий переходной и импульсной характеристик цепи позволяет свести расчет реакции цепи от действия непериодического сигнала произвольной формы к определению реакции цепи на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходный сигнал. При этом результирующая реакция линейной цепи находится (с использованием принципа наложения) как сумма реакций цепи на элементарные воздействия 1(t) или d(t). Между переходной g (t) и импульсной h (t) характеристиками линейной пассивной цепи существует определенная связь. Ее можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величины 1/t, сдвинутых друг относительно друга на время t (см. рис. 7.4):

т. е. единичная импульсная функция равна производной единичной функции. Так как рассматриваемая цепь предполагается линейной, то соотношение (8.1) сохраняется и для импульсных и переходных реакций цепи

т. е. импульсная характеристика является производной от переходной характеристики цепи.

Уравнение (8.2) справедливо для случая, когда g (0) = 0 (нулевые начальны е условия для цепи). Еслиже g (0) ¹ 0, то представив g (t) в виде g (t) = , где = 0, получим уравнение связи для этого случая: Для нахождения переходных и импульсных характеристик цепи можно использовать как классический, так и операторный методы. Сущность классического метода состоит в определении временной реакции цепи (в форме напряжения или тока в отдельных ветвях цепи) на воздействие единичной 1(t) или импульсной d(t) функции. Обычно классическим методом удобно определять переходную характеристику g (t), а импульсную характеристику h (t) находить с помощью уравнений связи (8.2), (8.3) или операторным методом.

· Анализ цепей при произвольных и импульсных воздействиях. Интеграл Дюамеля

 

 

 

 

 

Четырехполюсник

· Передаточная функция

В радиотехнических цепях сопротивления нагрузки обычно велики и не влияют на четырехполюсник либо сопротивление нагрузки стандартно и уже учтено в схеме четырехполюсника.

Тогда четырехполюсник может характеризоваться одним параметром, устанавливающим связь между выходным и входным напряжениями при пренебрежении током нагрузок. При синусоидальном сигнале такой характеристикой является передаточная функция цепи (коэффициент передачи), равная отношению комплексной амплитуды сигнала на выходе к комплексной амплитуде сигнала на входе: , где – фазово-частотная характеристика, - амплитудно-частотная характеристика цепи.

 

· Частотные характеристики

См. предыдущий вопрос.

 

 

· Интегрирующие и дифференцирующие цепи

Рассмотрим RC-цепь, изображенную на рис. 3.20,а. Пусть на входе этой цепи действует напряжение u1(t).

Рис. 3.20. Дифференцирующие RC-(а) и RL-(б) цепи.

Тогда для этой цепи справедливо соотношение

и с учетом преобразований будем иметь

(3.114)

 

Если для данного сигнала выбрать постоянную времени цепи τ=RC настолько большим, что вкладом второго члена правой части (3.114) можно пренебречь, то переменная составляющая напряжения uR≈u1. Это значит, что при больших постоянных времени напряжение на сопротивлении R повторяет входное напряжение. Такую цепь применяют тогда, когда необходимо передать изменения сигнала без передачи постоянной составляющей.

При очень малых значениях τ в (3.114) можно пренебречь первым слагаемым. Тогда

(3.115)

т. е. при малых постоянных времени τ RC-цепь (рис. 3.20,а) осуществляет дифференцирование входного сигнала, поэтому такую цепь называют дифференцирующей RC-цепью.

Аналогичными свойствами обладает и RL-цепь (рис. 3.20,б).

Рис. 3.21. Частотные (а) и переходная (б) характеристики дифференцирующих цепей.

Сигналы при прохождении через RС- и RL-цепи называют быстрыми, если

,

или медленными, если

.

Отсюда следует, что рассмотренная RC-цепь дифференцирует медленные и пропускает без искажения быстрые сигналы.

Для гармонической э. д. с. аналогичный результат легко получить, вычисляя коэффициент передачи цепи (рис. 3.20,а) как коэффициент передачи делителя напряжения со стационарными сопротивлениямиR и XC=1/ωC:

(3.116)

При малых τ, а именно когда τ<<1/ω, выражение (3.116) преобразуется в

.

При этом фаза выходного напряжения (аргумент K) равна π/2. Сдвиг гармонического сигнала по фазе на π/2 эквивалентен его дифференцированию. При τ>>1/ω коэффициент передачи K≈1.

В общем случае модуль коэффициента передачи (3.116), или частотная характеристика цепи (рис. 3.20,а):

(3.118)

а аргумент K, или фазовая характеристика этой цепи:

(3.119)

Эти зависимости показаны на рис. 3.21,а.

Такими же характеристиками обладает RL-цепь на рис. 3.20,б с постоянной времени τ=L/R.

Если в качестве выходного сигнала взять единичный скачок напряжения , то интегрированием уравнения (3.114) можно получить переходную характеристику дифференцирующей цепи, или временную зависимость выходного сигнала при единичном скачке напряжения на входе:

(3.120)

График переходной характеристики показан на рис. 3.21,б.

 

 

Рис. 3.22. Интегрииующие RC-(а) и LC-(б) цепи.

Рассмотрим RC-цепь, изображенную на рис. 3.22,а. Она описывается уравнением

или

(3.121)

При малых τ=RC (для «медленных» сигналов) uC≈u1. Для «быстрых» сигналов напряжение u1 интегрируется:

(3.122)

Поэтому RC-цепь, выходное напряжение которого снимается с емкости C называют интегрирующей цепью.

Коэффициент передачи интегрирующей цепи определяется выражением

(3.123)

При ω<<1/τ K≈1.

Частотная и фазовая характеристики описываются соответственно выражениями

(3.124)

(3.125)

Рис. 3.23. Частотные (а) и переходная (б) характеристики интегрирующих цепей.

и изображены на рис. 3.23,а. Переходная характеристика (рис. 3.23,б) получается интегрированием (3.121) при :

(3.126)

При равных постоянных времени такими же свойствами обладает RL-цепь, изображенная на рис. 3.22,б.

 

· Уравнение в форме А

При анализе электрических цепей в задачах исследования взаимосвязи между переменными (токами, напряжениями, мощностями и т.п.) двух каких-то ветвей схемы широко используется теория четырехполюсников. Четырехполюсник – это часть схемы произвольной конфигурации, имеющая две пары зажимов (отсюда и произошло его название), обычно называемые входными и выходными.

Примерами четырыхполюсника являются трансформатор, усилитель, потенциометр, линия электропередачи и другие электротехнические устройства, у которых можно выделить две пары полюсов.

В общем случае четырехполюсники можно разделить на активные, в структуру которых входят источники энергии, и пассивные, ветви которых не содержат источников энергии.

Ниже будут рассмотрены элементы теории пассивных четырехполюсников.

Для записи уравнений четырехполюсника выделим в произвольной схеме ветвь с единственным источником энергии и любую другую ветвь с некоторым сопротивлением (см. рис. 1,а).

В соответствии с принципом компенсации заменим исходное сопротивление источником с напряжением (см. рис. 1,б). Тогда на основании метода наложения для цепи на рис. 1,б можно записать

;

(1)

 

.

(2)

Решая полученные уравнения (1) и (2) относительно напряжения и тока на первичных зажимах, получим

;

или

;

(3)

·

,

(4)

где ; ; ; 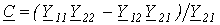- коэффициенты четырехполюсника.

Учитывая, что в соответствии с принципом взаимности , видно, что коэффициенты четырехполюсника связаны между собой соотношением

.

(5)

Уравнения (3) и (4) представляют собой основные уравнения четырехполюсника; их также называют уравнениями четырехполюсника в А-форме (см. табл. 1). Вообще говоря, существует шесть форм записи уравнений пассивного четырехполюсника. Действительно, четырехполюсник характеризуется двумя напряжениями и и двумя токами и . Любые две величины можно выразить через остальные. Так как число сочетаний из четырех по два равно шести, то и возможно шесть форм записи уравнений пассивного четырехполюсника, которые приведены в табл. 1. Положительные направления токов для различных форм записи уравнений приведены на рис. 2. Отметим, что выбор той или иной формы уравнений определяется областью и типом решаемой задачи.

 

Таблица 1. Формы записи уравнений пассивного четырехполюсника

Форма	Уравнения	Связь с коэффициентами основных уравнений
А-форма	;

· Электрические фильтры

Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания и нагрузкой и служащий для беспрепятственного (с малым затуханием) пропускания токов одних частот и задержки (или пропускания с большим затуханием) токов других частот.

Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием), называется полосой пропускания или полосой прозрачности; диапазон частот, пропускаемых с большим затуханием, называется полосой затухания или полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.

В качестве пассивных фильтров обычно применяются четырехполюсники на основе катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров, используемых при больших сопротивлениях нагрузки.

Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.

Для упрощения анализа будем считать, что фильтры составлены из идеальных катушек индуктивности и конденсаторов, т.е. элементов соответственно с нулевыми активными сопротивлением и проводимостью. Это допущение достаточно корректно при высоких частотах, когда индуктивные сопротивления катушек много больше их активных сопротивлений (), а емкостные проводимости конденсаторов много больше их активных проводимостей ().

Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной Т- или П-образной схеме, т.е. при или (см. лекцию №14). В этой связи при изучении фильтров будем использовать введенные в предыдущей лекции понятия коэффициентов затухания и фазы.

Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.

 

Таблица 1. Классификация фильтров

Название фильтра	Диапазон пропускаемых частот
Низкочастотный фильтр (фильтр нижних частот)
Высокочастотный фильтр (фильтр верхних частот)
Полосовой фильтр (полосно-пропускающий фильтр)
Режекторный фильтр (полосно-задерживающий фильтр)	и , где

В соответствии с материалом, изложенным в предыдущей лекции, если фильтр имеет нагрузку, сопротивление которой при всех частотах равно характеристическому, то напряжения и соответственно токи на его входе и выходе связаны соотношением

. .

(1)

В идеальном случае в полосе пропускания (прозрачности) 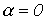, т.е. в соответствии с (1) , и . Следовательно, справедливо и равенство , которое указывает на отсутствие потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания (в полосе затухания) в идеальном случае , т.е. и .

Рассмотрим схему простейшего низкочастотного фильтра, представленную на рис. 1,а.

Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)

или конкретно для фильтра на рис. 1,а

;

(2)

·

;

(3)

·

.

(4)

 

Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что

.

Однако в соответствии с (2) 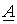- вещественная переменная, а следовательно,

.

(5)

Поскольку в полосе пропускания частот коэффициент затухания 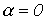, то на основании (5)

.

Так как пределы изменения : , - то границы полосы пропускания определяются неравенством

,

которому удовлетворяют частоты, лежащие в диапазоне

.

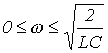(6)

Для характеристического сопротивления фильтра на основании (3) и (4) имеем

.

(7)

Анализ соотношения (7) показывает, что с ростом частоты w в пределах, определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается до нуля, оставаясь активным. Поскольку, при нагрузке фильтра сопротивлением, равным характеристическому, его входное сопротивление также будет равно , то, вследствие вещественности , можно сделать заключение, что фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших , как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.

На рис. 2 приведены качественные зависимости и .

Следует отметить, что вне полосы пропускания . Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство

.

(8)

Так как вне полосы прозрачности , то соотношение (8) может выполняться только при .

В полосе задерживания коэффициент затухания определяется из уравнения (5) при . Существенным при этом является факт постепенного нарастания , т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания будет отличен от нуля.

Другим вариантом простейшего низкочастотного фильтра может служить четырехполюсник по схеме на рис. 1,б.

Схема простейшего высокочастотного фильтра приведена на рис. 3,а.

Для данного фильтра коэффициенты четырехполюсника определяются выражениями

;

(9)

·

;

(10)

·

.

(11)

Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)

.

Данному неравенству удовлетворяет диапазон изменения частот

.

(12)

Характеристическое сопротивление фильтра

,

(13)

·

изменяясь в пределах от нуля до с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с 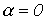в ограниченном диапазоне частот.

Вне области пропускания частот определяется из уравнения

(14)

при . Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.

Качественный вид зависимостей и для низкочастотного фильтра представлен на рис. 4.

Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.

Полосовой фильтр формально получается путем последовательного соединения низкочастотного фильтра с полосой пропускания 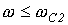и высокочастотного с полосой пропускания , причем . Схема простейшего полосового фильтра

приведена на рис. 5,а, а на рис. 5,б представлены качественные зависимости для него.

У режекторного фильтра полоса прозрачности разделена на две части полосой затухания. Схема простейшего режекторного фильтра и качественные зависимости для него приведены на рис.6.

В заключение необходимо отметить, что для улучшения характеристик фильтров всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой каскадно включенные четырехполюсники. При обеспечении согласованного режима работы всех n звеньев схемы коэффициент затухания 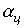такого фильтра возрастает в соответствии с выражением , что приближает фильтр к идеальному.

 

 

Нелинейные цепи

· Основные понятия и определения

Нелинейным элементом электрической цепи считается элемент, значения параметров которого зависят от значения тока данного элемента или напряжения на его выводах.

К нелинейным элементам электрических цепей относятся разнообразные полупроводниковые приборы, устройства, содержащие намагничивающие обмотки с ферромагнитными магнитопроводами (при переменном токе), лампы накаливания, электрическая дуга и др.

Нелинейные элементы дают возможность решать многие технические задачи, так, с помощью нелинейных элементов можно осуществить преобразование переменного тока в постоянный, усиление электрических сигналов, генерирование электрических сигналов различной формы, стабилизацию тока и напряжения, изменение формы сигнала и т.д. Нелинейные элементы широко используются в радиотехнических устройствах, в устройствах промышленной электроники, автоматики, измерительной и вычислительной техники.

Важнейшей характеристикой нелинейных элементов является вольт-амперная характеристика (в.а.х.), представляющая собой зависимость между током нелинейного элемента и напряжением на его выводах.

ВАХ нелинейных элементов весьма разнообразны и для некоторых из них представлены на рис. 1.29 а...д.

Там же приведены условные графические обозначения соответствующих элементов. Условное обозначение любого нелинейного резистивного элемента показано на рисунке 1.30.а. Имея в.а.х. нелинейного элемента, можно определить его сопротивления при любых значениях тока или напряжения. Различают два вида сопротивлений нелинейных элементов: статическое и дифференциальное.

Статическое сопротивление дает представление о соотношении конечных значений напряжения и тока нелинейного элемента и определяется в соответствии с законом Ома. Например, для точки А в.а.х. (рис.1.29.а) статическое сопротивление

где m_U и m_I -масштабные коэффициенты напряжения и тока.

Дифференциальное сопротивление позволяет судить о соотношении приращений напряжения и тока и определяется следующим образом:

К нелинейным электрическим цепям, то есть к цепям, содержащим нелинейные элементы, применимы основные законы электрических цепей: законы Ома и законы Кирхгофа, которые записываются для мгновенных значений токов и напряжений. Для расчета нелинейных электрических цепей применяется в большинстве случаев графоаналитический метод. Кроме того используется метод кусочно - линейной аппроксимации, когда в предлагаемом диапазоне изменения тока или напряжения нелинейного элемента его в.а.х. можно заменить прямой линией. При этом расчет можно производить и аналитическим методом. Следует отметить, что к той части электрической цепи, которая содержит только линейные элементы, применимы все методы расчета и преобразования электрических цепей, рассмотренные ранее.

 

· Графический и графоаналитический методы расчета

Предположим, что имеется электрическая цепь, схема которой приведена на рис. 1.30, а. В этой цепи нелинейный резистивный элемент r соединен с активным линейным двухполюсником A, который может быть любой сложности.

Расчет данной электрической цепи следует начать с замены активного двухполюсника эквивалентным генератором с параметрами E_экв=U_x и r_0экв (рис. 1.30, б) согласно методу эквивалентного генератора. Для дальнейшего расчета целесообразно воспользоваться методом графического решения двух уравнений с двумя неизвестными. Одним из уравнений следует считать зависимость I(U) нелинейного элемента, которой соответствует его в.а.х., приведенная на рис.1.30в. Другое уравнение, связывающее тот же ток I и то же напряжение U, нетрудно получить по второму закону Кирхгофа. Применив его к цепи с эквивалентным генератором (рис. 1.30, б), получим:

Поскольку зависимость I=f(U) линейная, график I=f(U) может быть построен по двум точкам (рис.1.30,в). Например, в режиме холостого хода эквивалентного генератора I=0 и U=U_x=E_экв, в режиме короткого замыкания U=0, I=I_к=E_экв/r_0экв.

Очевидно, искомые ток I и напряжение U определяются точкой Б пересечения в.а.х. I(U) нелинейного элемента и графика I=f(U) эквивалентного генератора.

Если к двухполюснику будут подключены два нелинейных элемента r₁ и r₂, соединенные последовательно (рис. 1.31 а), то перед расчетом согласно методике, изложенной выше, необходимо заменить их эквивалентным нелинейным элементом r_э (рис. 1.31 б) с эквивалентной в.а.х. I(U) (рис.1.31в). Построение эквивалентной в.а.х. I(U) производится на основании следующего соображения: при любом значении тока I напряжение U равно сумме напряжений U₁ и U₂ нелинейных элементов (рис. 1.31а), то есть

Задавшись несколькими значениями тока I по в.а.х. I(U₁) и I(U₂) нелинейных элементов r₁ и r₂, находят соответствующие напряжения U₁ и U₂, после чего согласно выражению (1.50) определяют напряжение U и строят в.а.х. I(U). На рис. 1.31, в показано в качестве примера определение при токе I напряжение U одной из точек (А) в.а.х. I(U).

Когда двухполюсник представляет собой источник с заданным напряжением, после построения I(U) можно при любом напряжении U найти ток I, а затем с помощью в.а.х. I(U₁) и I(U₂) напряжения U₁ и U₂.

При параллельном соединении двух нелинейных элементов (рис.1.32) для определения в.а.х. I(U) эквивалентного нелинейного элемента r_э (рис.1.33) необходимо воспользоваться тем, что при любом напряжении U токи связаны соотношением:

·

Задавшись несколькими значениями напряжения U, по в.а.х. I(U₁) иI₂ (U) (рис.1.33б) нелинейных элементов r₁ и r₂ находят соответствующие токи I₁ и I₂, после чего согласно (1.51) определяют ток I и строят в.а.х. I(U).

При смешанном соединении нелинейных элементов следует сначала построить в.а.х. участка с параллельным соединением элементов. После этого строят в.а.х. всей цепи. Имея в распоряжении все в.а.х., нетрудно определить токи и напряжения всех элементов цепи.

 

 

Магнитные цепи

· Основные понятия и определения

Магнитная цепь (МЦ) – часть электротехнического устройства, предназначенного для создания в определенном месте пространства магнитного поля требуемой интенсивности и направленности. Магнитные цепи составляют основу практически всех электротехнических устройств и многих измерительных приборов.

В составе МЦ имеются элементы, возбуждающие магнитное поле (одна или несколько намагничивающих обмоток или постоянные магниты) и магнитопровод, выполненный в основном из ферромагнитных материалов. Использование ферромагнетиков обусловлено их способностью многократно усиливать внешнее (по отношению к ним) магнитное поле, создаваемое намагничивающими обмотками или постоянными магнитами. Ферромагнетики отличает высокая магнитная проницаемость по сравнению с окружающей средой, что дает возможность концентрировать и направлять магнитные поля.

На рис. 1.1 в качестве примера представлены МЦ некоторых электромагнитных устройств: а – машин постоянного тока, б – электромагнитного реле, в – трансформатор, г и д – тормозных электромагнитов, е – магнитоэлектрического измерительного прибора. Цифрой 1- обозначены ферромагнитные части магнитопроводов, 2 – воздушные зазоры, 3 – намагничивающие катушки, 4 – постоянный магнит.

 

 

МЦ с постоянной МДС называются цепи, в которых магнитное поле возбуждается постоянными токами намагничивающих обмоток или постоянными магнитами.

При анализе и расчете магнитных цепей пользуются следующими величинами, характеризующими магнитное поле:

– вектор магнитной индукции. Характеризует интенсивность и направленность магнитного поля в данной точке пространства. Единица измерения – тесла (1 Тл =1 = 1 )

– вектор напряженности магнитного поля в данной точке. Единица измерения – ампер на метр (А/м).

Отношение – абсолютная магнитная проницаемость. Для вакуума, а также для любых неферромагнитных материалов принимается равной m0= 4π·10-7 Гн/м; отношение – относительная магнитная проницаемость (для конкретных ферромагнетиков может доходить до 104 – 106).

Ф – магнитный поток – поток вектора магнитной индукции через площадь S (рис. 1.1), единица измерения вебер (1Вб=1Тл×1м2).

1.1.

В случае однородного магнитного поля, когда B=const в любой точке поля и вектор магнитной индукции ^S (Ða=0), магнитный поток

Ф=B×S 1.2.

Расчет магнитной цепи невозможен, если неизвестна основная кривая намагничивания (ОКН) ферромагнетика, используемого в магнитопроводе.

ОКН задается в справочной литературе на электротехнические материалы как зависимость В(Н) либо в табличной форме, либо графически (рис. 1.3).

Отметим, что на участке оа, отношение const. – магнитная цепь не насыщена. При дальнейшем увеличении Н темп увеличения индукции В снижается и прекращается полностью, когда наступает магнитное насыщение материала магнитопровода.

Закон полного тока

 

· Цепи с постоянной МДС

См. предыдущий вопрос.

 

 

· Катушка со сталью в цепи переменного тока