Для цепи на рис. 21 можно записать
;
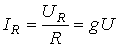, где 
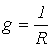[См] – активная проводимость;
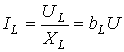, где 
[См] – реактивная проводимость катушки индуктивности.
Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме
,
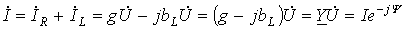где 
;
- комплексная проводимость;
.
Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.
|
Выражение комплексного сопротивления цепи на рис. 21 имеет вид:
.
· Мощность в цепи
Пусть в цепи (рис. 2.15) ток равен
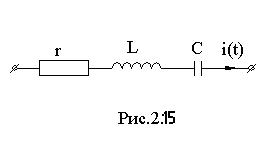
Мгновенное напряжение будет сдвинуто по отношению к току на угол ψ, отличный от 0 и ±π/2. Мгновенная мощность для этой цепи примет вид: тогда:
Выразим сопротивления через модуль Z:
Подставив (14) в (13), получим:
Временные диаграммы i(t),u(t),p(t) приведены на рис. 2.16.
Мощность p(t) имеет постоянную составляющую, т.е. среднюю мощность, или активную мощность:
и переменную составляющую. Амплитуда переменной составляющей
называется полной мощностью, измеряется в вольт-амперах. Мощности P и S связаны по закону треугольника мощностей, рис. 2.17.
Третья составляющая в этом треугольнике – мощность реактивная:
Реактивная мощность измеряется в вольт-амперах реактивных; полезная мощность измеряется ваттметром.
· Расчет цепей
При анализе цепей синусоидального тока широко применяются векторные диаграммы и комплексные числа. Сами по себе векторные диаграммы зачастую служат для иллюстрации результатов теоретических исследований и решения задач. Они помогают лучше понять сущность изучаемых процессов и наглядно представить соотношения и связи напряжений и токов на различных участках с параметрами цепи.
Во многих случаях векторные диаграммы, построенные предварительно по изложенным выше правилам без каких-либо вычислений, являются основой для вывода из них конкретной методики решения данной задачи. Возможны также привязка векторной диаграммы к комплексным осям, выражение векторов комплексными числами и дальнейший расчет в символической форме. Принципиального отличия между методом векторных диаграмм и символическим нет. Как мы видели раньше, за аналитическими действиями с комплексными числами кроются определенные геометрические операции с векторами.
Следует также помнить, что никакого физического содержания векторы и комплексные числа в себе не несут. Это чисто математические абстракции, необходимые для анализа.
Символический метод базируется на законах Ома и Кирхгофа, которые в символической форме записываются точно так же, как в цепях постоянного тока. Поэтому все изложенные ранее методы расчета цепей постоянного тока, вытекающие из этих законов, применимы и для расчета в символической форме цепей синусоидального тока.
Пример.
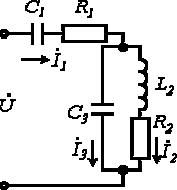
Дано:
|   
| |
  
| ||
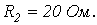
| Определить: | 1) полное комплексное сопротивление цепи  ;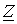
| |
2) токи 
| ||
| Рис. 2 |
Решение:
1. 
.
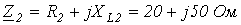2. 
.
3. 
.
4. Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда
.
5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то
6. 
.
7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме
|
|
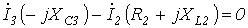
или после подстановки численных значений параметров схемы
· Резонансные явления (резонанс напряжений, резонанс токов)
Реактивные сопротивления и проводимость являются частотно-зависимыми величинами. Следовательно, при последовательном или параллельном соединении элементов L и C возможна на какой-то частоте полная компенсация реактивных сопротивлений или проводимостей. Режим, при котором наступает компенсация, называют резонансом. При резонансе входное сопротивление цепи становится активным, входное напряжение совпадает по фазе с входным током, а полная мощность будет активной. Угловая частота, ω0, при которой наступает резонанс, называется резонансной или собственной угловой частотой цепи. Различают две разновидности резонанса: резонанс напряжений и резонанс токов.
Резонанс напряжений.
Может возникнуть в цепи с последовательным соединением L и C рис. 2.20а.
Для этой цепи запишем:
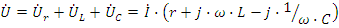
Условие резонанса:
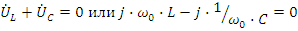
откуда резонансная частота 
. Настройку цепи в резонанс, изменение параметров цепи при частотах, отличных от резонансной можно увидеть, если построить частотные характеристики сопротивлений, тока в цепи и напряжений на r,L,C. На рис. 2.20б, в, г приведены частотные характеристики реактивных сопротивлений
суммарного реактивного сопротивления:
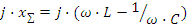
модуля полного сопротивления:
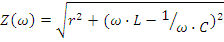
модуля входного тока:
а также АЧХ напряжений:
По графику j⋅xΣ(ω) определена резонансная частота ω0, по графику Z(ω) можно увидеть, что сопротивление цепи при резонансе минимально и равно активному сопротивлению, по графику I(ω) - что ток в цепи при резонансе максимален. Графики Ur(ω), UL(ω), UC(ω) имеют ярко выраженный избирательный характер, т.е. имеют максимальные значения на резонансной частоте или вблизи нее. Можно также отметить, что напряжения UC, UL при резонансе могут превышать значение входного напряжения. Это хорошо иллюстрируется с помощью векторных диаграмм напряжения приведенных на рис.2.20д, е, ж при частотах ω≤ω0, ω=ω0 и ω≥ω0. Обратите также внимание на значения угла φ на этих частотах и сопоставьте эти значения с характером реактивных сопротивлений на соответствующих частотах. При частотах ω≤ω0, реактивное сопротивление носит емкостной характер и cos(φ)≤0.
Резонанс токов.
Может возникнуть в цепи с параллельным соединением L и C рис. 2.21а.
Для этой цепи запишем уравнение по первому закону Кирхгофа:
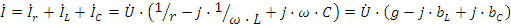
Компенсация реактивных проводимостей и реактивных токов:
произойдет на резонансной частоте
Для анализа явления резонанса токов построим частотные характеристики реактивных проводимостей, рис.2.21б, модуля полной проводимости:
модуль полного тока:
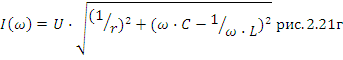
Здесь отмечена резонансная частота, полная проводимость цепи при резонансе минимальна и полный ток минимален. Векторные диаграммы токов, построенные для частот ω≤ω0, ω=ω0 и ω≥ω0 рис. 2.21е, д, ж, позволяют убедиться, что токи в катушке и конденсаторе могут значительно превышать полный ток.
