Перечень вопросов
Анализ цепей постоянного тока в установившемся режиме.
· Основные понятия и определения
· Основные законы
· Методы расчета (контурные токи, узловые потенциалы, эквивалентный генератор)
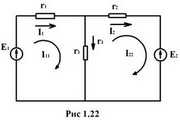
Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом расчета по законам Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурные токи, замыкающиеся в контурах. На рис. 1.22 в виде примера показана двухконтурная цепь, в которой I11 и I22 - контурные токи. Токи в сопротивлениях r1 и r2 равны соответствующим контурным токам; ток в сопротивлении r3 являющемся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви r3 встречно.
Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, то есть для электрической схемы с числом узлов q и числом ветвей p задача нахождения контурных токов сведется к решению системы p-q+1 уравнений. Так, в схеме рис. 1.22 q=2, p=3; следовательно, число уравнений равно 3-2+1=2 (число уравнений независимых контуров).
Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от заданного контурного тока в сопротивлениях, входящих в контур, берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис.1.22., где направление обоих контурных токов выбрано по ходу часовой стрелки.
Для заданной электрической схемы с двумя независимыми контурами (рис.1.22) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:
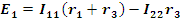
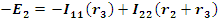
здесь (r1+r3) и (r2+r3) - собственные сопротивления контуров 1 и 2, r3 - общее сопротивление контуров 1 и 2. После определения контурных токов, легко найти и токи всех ветвей.
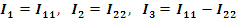
Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются напряжения в узлах электрической цепи относительно некоторого базисного узла. Эти искомые напряжения называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.
Напряжение на какой - либо ветви равно, очевидно, разности узловых напряжений концов данной ветви; произведение же этого напряжения на проводимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
При наличии одной ветви с э.д.с и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь, тогда напряжение данного узла становится известным и число неизвестных сокращается на одно.
Число неизвестных в методе узловых напряжений равно числу уравнений, которые надо составить для схемы по первому закону Кирхгофа. Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа, или если (q-1) < (p-q+1), или, что то же 2(q-1) < p, где q - число узлов, p - число ветвей.
На рис. 1.24 в виде примера изображена электрическая схема, содержащая три узла. Примем потенциал φ3=0 (базисный узел). Составим уравнения для узлов 1 и 2 по первому закону Кирхгофа:
Каждые из этих токов можно выразить через узловые потенциалы и э.д.с. ветвей:
Подставив (1.40) в (1.39), сгруппировав члены при φ1 и φ2 и перенеся члены с э.д.с. в правую часть, получим:
где
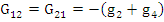
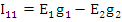
Таким образом, множителем при φ1, является коэффициент G11, равный сумме проводимостей всех ветвей, сходящихся в первом узле (1.42). G12 равняется сумме проводимостей всех ветвей, соединяющих узел 1 с узлом 2, взятой со знаком минус. Ток I11 называют узловым током первого узла. Это расчетная величина, равная алгебраической сумме токов, полученной от деления э.д.с. ветвей, подходящих к узлу 1, на величину сопротивлений этих ветвей. Если э.д.с. направлена к узлу, то берется в I11 со знаком плюс, если от узла, то со знаком минус. Так же определяют G22, G21, I22 (см. 1.42).Если между какими-либо двумя узлами нет ветви, то соответствующая проводимость равна нулю. Решив систему (1.41) относительно φ1, и φ2, определим узловые напряжения цепи. Искомые токи определяют либо по закону Ома, либо по второму закону Кирхгофа для участка цепи, содержащей э.д.с.
Частным случаем метода узловых напряжений является метод двух узлов.
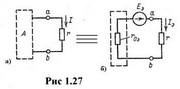
Метод эквивалентного генератора используется в случае, когда необходимо найти ток, напряжение или мощность в одной ветви. При этом вся остальная часть цепи, к которой подключена данная ветвь, рассматривается в виде двухполюсника (рис.1.27 а). Двухполюсник называют активным, если он содержит источники электрической энергии, и пассивным - в противоположном случае. Будем обозначать активный двухполюсник буквой А, а пассивный - буквой П.
Различают две модификации метода эквивалентного генератора: метод эквивалентного источника напряжения и метод эквивалентного источника тока.
Рассмотрим метод эквивалентного источника напряжения. Этот метод базируется на теореме Тевенина, согласно которой ток в любой ветви линейной электрической цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником (генератором) напряжения. Э.д.с. этого источника равна напряжению холостого хода на зажимах разомкнутой ветви, а внутреннее сопротивление равно эквивалентному входному сопротивлению пассивного двухполюсника со стороны разомкнутой ветви (рис. 1.27, б).
Опуская доказательство этой теоремы, после замены активного двухполюсника эквивалентным источником в соответствии с этой схемой имеем:
· Электрическая энергия и мощность
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
.
Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
, где 
— электрическое сопротивление.
Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
, где 
— ЭДС.
Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность 
прибавляется к поглощаемой или вычитается из отдаваемой.
На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия
W= 
Rt.
Скорость преобразования электрической энергии в другие виды представляет электрическую мощность
.
Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.
.
Электрические цепи синусоидального тока
· Основные понятия и определения
Резистор, индуктивность и емкость являются пассивными элементами электрической цепи.
Резистор r или активное сопротивление цепи – это элемент, в котором происходит рассеивание энергии в виде тепла или превращение электрической энергии в другой вид энергии: световую, химическую или механическую. Индуктивность L и емкость C называются реактивными элементами цепи, в них происходят накапливание энергии в виде магнитного или электрического поля; рассеивание энергии в таких элементах отсутствует.
Индуктивный элемент учитывает явления накапливания энергии магнитного поля и характеризуется зависимостью потокосцепления ψ от тока i:
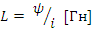
Мгновенное значение напряжения на индуктивности:
Здесь eL - ЭДС, наводимая изменяющимся во времени магнитным потоком.
Емкость отражает явление накапливания энергии электрического поля и характеризуется зависимостью заряда q от напряжения: 
Мгновенное значение напряжения на конденсаторе:
· Символический метод расчета
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.
1. Первый закон Кирхгофа в комплексной форме:
 .
|
2. Второй закон Кирхгофа в комплексной форме:
|
или применительно к схемам замещения с источниками ЭДС
 .
|
Ток
можно записать по формуле Эйлера:
С учетом (2) уравнение (1) примет вид:
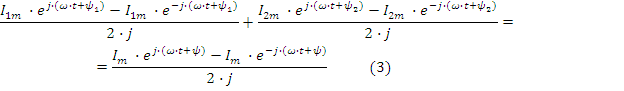
Уравнение (3) содержит два типа комплексных чисел:
и оно может быть записано для каждой группы в отдельности, например:
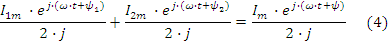
Исключая общие множители ej⋅ω⋅t и 1/2⋅j получим:
Комплексное число 
называется током в комплексной форме или комплексом тока по максимальному значению. Здесь Im модуль комплекса по максимальному значению, а ψ фаза комплекса. Если за модуль комплекса принять не амплитудное, а действующее значение, то получим комплекс по действующим значениям I=I⋅ej⋅ψ или просто комплекс тока.
Уравнение (5) для комплексов тока примет вид:
Геометрическая интерпретация уравнения (6) на комплексной плоскости приведена на рис.2.2б. Это так называемая комплексная векторная диаграмма является с учетом масштаба точным аналогом векторной диаграммы, приведенной на рис.2.2а. Комплекс тока I называют символом мгновенного тока i(t),а метод составления уравнений в комплексной форме – комплексным или символическим.
· Изображение токов и напряжений комплексными числами
Запишем комплексное число в виде
I m = Imеj α = Im cos α + jIm sin α
Допустим, что вектор комплексного числа Im вращается с постоянной угловой частотой ω и угол α = ω t + ψ. Тогда
I m = Imеj (ω t + ψ) = Im cos (ω t + ψ) + jIm sin (ω t + ψ).
Слагаемое Im cos (ω t + ψ) представляет собой действительную часть комплексного числа и обозначается
Im cos (ω t + ψ) = Re Imеj (ω t + ψ).
Слагаемое Im sin (ω t + ψ) есть коэффициент при мнимой части комплексного числа и обозначается
Im sin (ω t + ψ) = Im Imеj (ω t + ψ).
Легко видеть, что коэффициент при мнимой части комплексного числа представляет собой выражение мгновенного значения синусоидального тока
i = Im sin (ω t + ψ)
и является проекцией вращающегося вектора I m на мнимую ось комплексной плоскости.
Синусоидально изменяющиеся по времени величины изображаются на комплексной плоскости для момента времени t = 0. Тогда комплексная амплитуда I m записывается в виде
I m = Imej ψ,
где I m — комплексная амплитуда; Im - ее модуль, а ψ - угол между вектором I m, и действительной осью.
Таким образом, комплексная амплитуда изображает синусоидальный ток на комплексной плоскости для момента времени t = 0.
Допустим, что в электрической цепи мгновенные значения напряжений и тока имеют выражения
и = Um sin(ω t + ψ1);
i = Im sin (ω t + ψ2).
Комплексные амплитуды напряжения и тока должны быть записаны в виде
U m = Umej ψ1;
I m = Imej ψ2;
где Um и Im — соответственно модули комплексных амплитуд напряжений и тока; ψ1 и ψ2 — начальные фазы U m и I m относительно действительной оси (углы начальных фаз).
Обычно принято выражать в виде комплексных чисел не амплитуды, а действующие значения напряжений и токов:
| U = | Um | ej ψ1 - Uej ψ1, I = | Im | ej ψ2 = Iej ψ2. |
| √2 | √2 |
· Законы Кирхгофа в комплексной форме
Первый закон Кирхгофа:
Второй закон Кирхгофа:
Уравнения энергетического баланса:
· Векторные диаграммы
Резистор
Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение 
(см. рис. 1), то ток i через него будет равен
 .
| (1) |
Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.
Из (1) вытекает:
;
.
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
;
,
- разделим первый из них на второй:
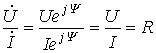
или
 .
| (2) |
Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.
Конденсатор
Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение (см. рис. 4), то ток i через него будет равен
 .
| (3) |
Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на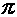 
/2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.
Из (3) вытекает:
;
.
Введенный параметр 
называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, 
имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при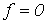 
конденсатор представляет разрыв для тока, а при 
.
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
;
,
- разделим первый из них на второй:
или
 .
| (4) |
В последнем соотношении 
- комплексное сопротивление конденсатора. Умножение на 
соответствует повороту вектора на угол 
по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.
3. Катушка индуктивности 
Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением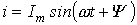 
. Тогда для напряжения на зажимах катушки индуктивности можно записать
 .
| (5) |
Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на 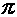/2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.
Из (5) вытекает:
|
.
Введенный параметр 
называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при 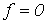катушка индуктивности не оказывает сопротивления протекающему через него току, и при 
.
Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам:
;
,
разделим первый из них на второй:
или
 .
| (6) |
В полученном соотношении 
- комплексное
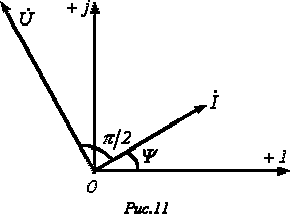
сопротивление катушки индуктивности. Умножение на 
соответствует повороту вектора на угол против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11.
