| Вид продукции | Выпуск продукции в I квартале, тыс. руб. | Увеличение (+) или уменьшение (—) выпуска продукции во II квартале по сравнению с I кварталом, % |
| Рельсы трамвайные | 32 100 | +2,0 |
| Чугун литейный | 12 300 | -5,0 |
| Железо листовое | 15 600 | + 2,5 |
Для определения изменения физического объема продукции в целом по предприятию используется формула среднего взвешенного арифметического индекса (8.19), так как по условию задачи известны индивидуальные индексы физического объема. Индивидуальные индексы по видам продукции:
рельсы трамвайные: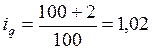 
;
чугун литейный: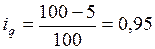 
;
железо листовое: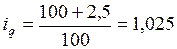 
.
Тогда средний взвешенный арифметический индекс равен:
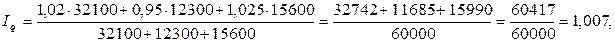
или 100,7%.
Следовательно, физический объем продукции в целом по предприятию увеличился на 0,7%.
Задача 8
Необходимо определить общие индексы физического объема потребления товаров и услуг населением, исходя из данных о расходах населения республики (табл.8.8).
Таблица 8.8
Динамика потребления населения
| Материальные блага и услуги | Стоимость приобретенных товаров и услуг в текущих ценах за период, ден.ед.: | Изменение цен, % | |
| Базисный период | Отчетный период | ||
| 1. Продовольственные товары 2. Непродовольственные товары 3. Платные услуги | + 7,5 +5,2 +7,8 |
Расчет ведем по средней геометрической взвешенной:
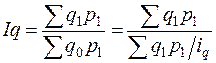
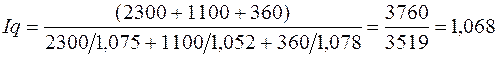или 106,8%
Следовательно, объем потребления всем населением материальных благ и услуг во втором периоде по сравнению с первым возрос на 6,8%.
Решение типовых задач по теме
СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ
Задача 1
Для установления факта наличия связи между временем вулканизации резины и ее сопротивлением разрыву построить график связи.
| Номер эксперимента | ||||||||||||
| Время вулканизации, мин | ||||||||||||
| Сопротивление разрыву, кг/см2 |
Как видно из данных таблицы, с увеличением времени вулканизации возрастает величина сопротивления резины разрыву. На рис. 9.2 представим график связи.
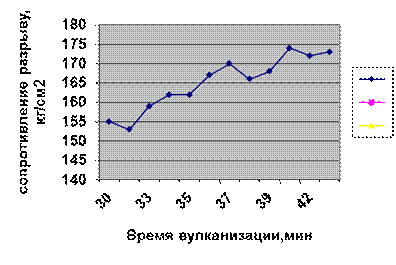
Рис. 9.2 Зависимость сопротивления резины разрыву от времени
вулканизации.
Эмпирическая линия связи приближается к прямой линии. Следовательно, можно считать наличие прямолинейной корреляции.
Задача 2
На основании выборочных данных о реализованной продукции (х) и затратах на производство продукции (у) предприятий легкой промышленности:
Таблица 9.5
Группировочная таблица исходных данных
| Затраты на производство, млрд. руб. | Реализованная продукция, млрд. руб. | ||||
| 0-1,4 | 1,4-2,8 | 2,8-4,2 | 4,2-5,6 | 5,6-7,0 | |
| 0-0,8 | |||||
| 0,8-1,6 | |||||
| 1,6-2,4 | |||||
| 2,4-3,2 | |||||
| 3,2-4,0 |
Необходимо вычислить статистические характеристики двумерной корреляционной модели.
Прежде всего, каждому интервалу значений рассматриваемых случайных величин поставим в соответствие середину соответствующего интервала (во вспомогательной таблице средины интервалов обозначены уj \ хi).
Для каждого значения хi,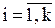 
, т.е. для каждого столбца вспомогательной таблицы частоты 
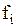, рассчитываются как 
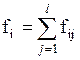, где суммирование производится по всем значениям соответствующего столбца.
Аналогично, для каждого значения уj,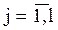 
, т.е. для каждой строки вспомогательной таблицы, частоты рассчитываются как 
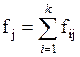, где суммирование производится по всем значениям соответствующей строки.
В седьмой строке и седьмом столбце вспомогательной таблицы помещаются произведения значений переменных на соответствующие частоты, т.е.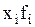 
и 
.
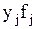В восьмой строке и восьмом столбце вспомогательной таблицы помещаются произведения квадратов значений переменных на соответствующие частоты, т.е.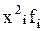 
и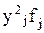 
.
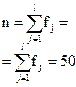
На основании данных вспомогательной таблицы рассчитываются средние значения по формуле средней арифметической взвешенной:
, 
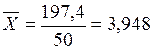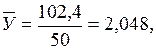
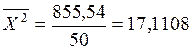
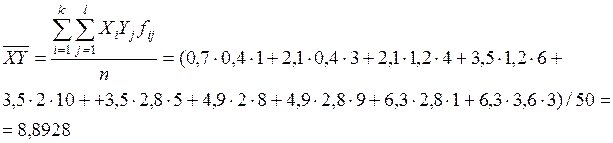
Дисперсии признаков при двумерном нормальном законе распределения случайных величин (X, Y)можно определить по формулам:
,
.
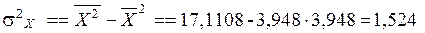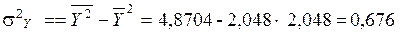Коэффициент корреляции рассчитывается по формуле (9.20):
.
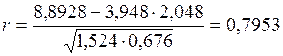Таким образом, между объемом реализованной продукции и затратами на ее производство наблюдается высокая сила связи.
Таблица 9.6
Вспомогательная таблица для решения примера
| Затраты на производство,млрд руб. | Середины интервалов | Реализованная продукция, млрд. руб. | Частота
| 
| 
| ||||
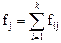
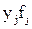
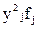
| хi уj | 0-1,4 | 1,4-2,8 | 2,8-4,2 | 4,2-5,6 | 5,6-7,0 | ||||
| 0,7 | 2,1 | 3,5 | 4,9 | 6,3 | |||||
| А | Б | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0,0-0,8 | 0,4 | 1,6 | 0,64 | ||||||
| 0,8-1,6 | 1,2 | 14,4 | |||||||
| 1,6-2,4 | |||||||||
| 2,4-3,2 | 2,8 | 117,6 | |||||||
| 3,2-4,0 | 3,6 | 10,8 | 38,88 | ||||||
Частота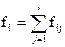 
| 
| 
| 
| ||||||
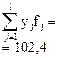
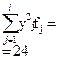
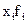
| 0,7 | 14,7 | 73,5 | 83,3 | 25,2 |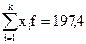 
| |||
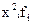
| 0,49 | 30,87 | 257,25 | 408,17 | 158,76 |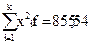 
|
Задача 3
Произвести расчет общей, межгрупповой и средней из внутригрупповых дисперсий по данным таблицы 9.7 (столбцы 1 и 2). Вычислить эмпирическое корреляционное отношение и коэффициент детерминации.
Общая дисперсия рассчитывается по формуле (9.3):
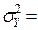(4+162,8+4,6+18,3+397,1+297,9+106,9+9,1+105,3+246,8+5,9+88,5+212,9)/20=82,2.
Средняя из внутригрупповых дисперсий рассчитывается по формуле (9.5):
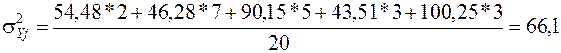
Таблица 9.7
Расчет дисперсий
| Группы предприятий по потерям рабочего времени, чел.-дней | Производительность по группам Yij | Средняя производительность по группам
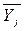
| Число предприятий в группе
| 
| 
| 
|
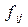
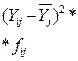
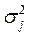
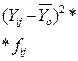
| 8,8-10,6 | 19,50 34,26 | 26,88 | 54,48 54,48 | 54,48 | 4,0 162,8 | |
| 10,6-12,4 | 20,43 25,78 35,59 | 24,81 | 76,46 16,15 231,34 | 46,28 | 4,6 18,3 397,1 | |
| 12,4-14,2 | 4,24 14,19 24,51 31,76 | 17,76 | 182,57 26,17 45,65 196,36 | 90,15 | 297,9 106,9 9,1 105,3 | |
| 14,2-16,0 | 5,79 19,78 | 15,12 | 87,01 43,51 | 43,51 | 246,8 5,9 | |
| 16,0-17,8 | 14,85 36,09 | 21,93 | 100,25 200,50 | 100,25 | 88,5 212,9 |
Таблица 9.8
