Решение типовых задач
Тема: Выборочное наблюдение
Задача 1.
Для примера, исследуем выборку из 20 предприятий по величине производительности труда (всех предприятий -100). Предприятий с низким уровнем производительности оказалось 2. С вероятностью 0,683 необходимо найти пределы, в которых можно ожидать долю предприятий со средним и высоким уровнем производительности. Выборка случайная, бесповторная. Имеются данные:
n =20 (шт.)
N =100 (шт.)
m =20-2=18 (шт.)
t =1
P(t) =0,683
w =18/20=0,9
Определим среднюю ошибку выборки:
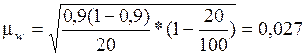или 2,7%
Рассчитаем предельную ошибку: 
Определим пределы, в которых можно ожидать долю предприятий с высоким и средним уровнем производительности:
С вероятностью 0,683, т.е. в 683 случаях из 1000, можно утверждать, что средний процент предприятий с высоким и средним уровнем производительности будет находиться в пределах от 87 до 93%.
Рассчитаем относительную ошибку:
= 3,63/21,51=0,169 или 16,9%,
= 0,03/0,9=0,033 или 3,3%
Следовательно, как для оценки средних показателей, так и для оценки доли, выборка репрезентативна.
Задача 2
Из партии деталей взята 20%-ная случайная бесповторная выборка для определения среднего веса детали. Результаты выборки следующие:
| Вес (г), х | 76-80 | 80-84 | 84-88 | 88-92 |
| Число деталей, f |
Определить с вероятностью 0,954 доверительные пределы, в которых лежит средний вес детали для всей партии.
Решение.
Доверительные интервалы для генеральной средней с вероятностью Р:
,
где 
— средний уровень признака по выборке:
г.
Определим численность генеральной совокупности:
.
Дисперсия выборки равна:
Предельная ошибка равна:
г.
При вероятности Р = 0,954 t = 2. Доверительные интервалы для генеральной средней с вероятностью Р = 0,954 следующие:
;
;
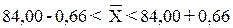На основе проведенной выборки сделаем вывод: установлен средний вес детали с возможным отклонением в ту или иную сторону не более, чем на 0,66 г, или в пределах от 83,34 до84,66 г, что можно утверждать с вероятностью 0,954, т.е. в 954 случаях из 1000.
Задача 3
Рассмотрим 20 из 100 единиц совокупности. Таким образом, мы имеем дело с выборкой. Исходя из предыдущих расчетов для ряда производительности труда, при условии, что отбор случайный, бесповторный, а вероятность равна 0,954, имеются следующие данные:
ден.ед.
шт.
n=20 шт.
ден. ед.
t=2
Тогда средняя ошибка выборки будет равна: 
.
Отсюда получим величину предельной ошибки:
.
Вычислим пределы для генеральной средней: 
.
На основе проведенной выборки сделаем вывод: установлена средняя производительность труда для предприятий с возможным отклонением в ту или иную сторону не более, чем на 3,63 ден.ед., или в пределах от 17,88 до 25,14 ден.ед., что можно утверждать с вероятностью 0,954, т.е. в 954 случаях из 1000.
Определим пределы, в которых можно ожидать суммарную производительность труда для всех предприятий генеральной совокупности:
Таким образом, суммарную производительность труда для всех предприятий, составляющих генеральную совокупность, можно ожидать в пределах от 1788 до 2514 ден.ед.
Далее определим пределы, в которых можно ожидать количество предприятий с высоким и средним уровнем производительности в генеральной совокупности:
Таким образом, среди ста предприятий генеральной совокупности количество предприятий, обладающих искомым признаком можно ожидать в пределах от 87 до 93.
Задача 4
На предприятии из партии продукции в количестве 20000 шт. деталей взято на выборку 2000 шт. (отбор случайный, бесповторный), из которых 50 шт. оказались бракованными.
Определить с вероятностью 0,997 пределы, в которых будет находиться процент брака для всей партии продукции.
Решение
Определяется доля бракованной продукции по выборке:
или 2,5%.
При вероятности Р(t) =0,997 t = 3,0.
Размер предельной ошибки:
,
или 1%.
Доверительные интервалы для генеральной доли с вероятностью Р(t) =0,997:
;
.
С вероятностью 0,997, т.е. в 997 случаях из 1000 можно утверждать, что средний процент бракованных деталей будет находиться в пределах от 1,5 до 3,5%.
Задача 5
По городской телефонной сети в порядке случайной выборки (механический отбор) произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора 7 минут при среднем квадратическом отклонении 2 минуты.
Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 15 секунд?
Решение
По условию задачи известны:
объем выборки п = 100;
выборочная средняя 
= 7 мин;
выборочное среднее квадратическое отклонение 
= 2 мин;
предельная ошибка выборки равна: 
= 15 сек = 0,25 мин.
Рассчитаем среднюю ошибку выборки:
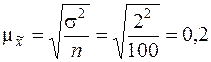мин.
Рассчитаем значение t:
Затем по таблице на основе значения t определяется вероятность того, что ошибка не превысит заданной величины.
При t =1,25 вероятность Р(t) = 0,789.
Задача 6
На основе выборочного обследования в отделении связи города предполагается определить долю поздравительной корреспонденции в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отравляемой корреспонденции не имеется.
Определить численность выборки, если результаты выборки дать с точностью до 1 % и гарантировать это с вероятностью 0,683.
Решение.
По условию задачи известны:
размер допустимой (предельной) ошибки 
= 1%, или 0,01;
при Р(t) =0,683 t= 1.
Так как значение w не дано, то следует ориентироваться на наибольшую дисперсию, которой соответствует значение w = 0,5.
Необходимая численность выборки равна:
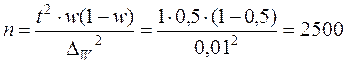единиц.
Таким образом, чтобы с заданной точностью определить долю поздравительных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной выборки отобрать 2500 писем.
Задача 7
В университете в порядке случайной бесповторной выборки было опрошено 100 студентов из 1000 и получены следующие данные о времени, потраченном на дорогу из дома в университет:
| Время на дорогу, ч | 0,6-0,8 | 0,8-1,0 | 1,0-1,2 | 1,2-1,4 |
| Число студентов |
Определить:
1) среднее время, потраченное на дорогу, для студентов данного университета, гарантируя результат с вероятностью 0,997;
2) долю студентов, потративших дорогу 1,2 часа и более, гарантируя результат с вероятностью 0,954;
3) необходимую численность выборки при определении среднего времени, потраченного на дорогу, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 0,02 часа;
4) необходимую численность выборки при определении доли
студентов, потративших на дорогу 1,2 часа и больше, чтобы с
вероятностью 0,954 предельная ошибка не превышала 4%.
Решение.
1. Доверительный интервал среднего размера времени на дорогу: .
Средний размер времени по выборке:
ч.
Дисперсия по выборке:
При вероятности Р (t) = 0,997 t = 3,0.
Предельная ошибка выборки равна:
Доверительные интервалы для генеральной средней:
1-0,15 
1+0,15.
0,85 1,15
Таким образом, среднее время, потраченное на дорогу, для студентов данного университета находится в пределах от 0,85 до 1,15 часа, это можно утверждать с вероятностью 0,997 или в 997 случаев из 1000.
2. Доля студентов, затрачивающих на дорогу 1,2 часа и более, по выборочным данным составляет:
.
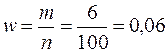При вероятности Р (t) = 0,954 t = 2,0.
Предельная ошибка доли:
.
Доверительные интервалы для генеральной доли:
;
.
Таким образом, доля студентов данного университета, тратящих на дорогу 1,2 часа и более, находится в интервале от 1,5% до 15%, что можно утверждать с вероятностью 0,954 или в 954 случаев из 1000.
3. Необходимая численность выборки для определения среднего месячного дохода определяется по формуле:
.
По условию задачи известны:
при вероятности Р = 0,954 t = 2
;
(по данным предыдущей выборки).
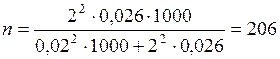чел.
Таким образом, в выборку необходимо отобрать 206 человек, что выполнялись указанные условия.
4. Необходимая численность выборки для определения доли студентов, тратящих на дорогу 1,2 часа и выше, определяется по формуле:
По условию задачи известны:
= 4%, или 0,04; при вероятности Р = 0,954 t = 2;
w = 0,06 (по данным предыдущей выборки).
человека.
Таким образом, в выборку необходимо отобрать 124 человека, что выполнялись указанные условия.
Задача 8
Операция шлифования при обработке детали № 18 производится в цехе на трех станках. Для определения процента брака для всей партии продукции, выработанной за день, проведена расслоенная (типическая) 10%-ная выборка. Отбор деталей из выработки каждого станка – случайный бесповторный; объем выборки пропорционален размеру выпуска. На первом станке было обработано 1500 деталей, на втором – 1800, на третьем – 1200 деталей. Число забракованных деталей в выборке: по первому станку –3, по второму – 4, по третьему – 2.
Определить:
1) доверительные интервалы, в которых с вероятностью 0,683 заключен процент брака для всей партии продукции;
2) вероятность того, что процент брака для всей партии продукции отличается от полученного по выборке не более чем на 0,5 %.
Решение.
1. Рассчитаем общий объем генеральной совокупности –
N = N1 + N2 + N 3 = 1500 + 1800 + 1200 = 4500 деталей.
Численность выборки:
деталей,
в том числе по станкам численность выборки рассчитывается по формуле:
,
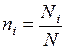отсюда:
n1 = 150 деталей,
n2 = 180 деталей,
n 3 =120 деталей.
Доверительные интервалы процента брака для всей партии продукции:
,
где W – процент брака для всей выборочной совокупности:
;
— предельная ошибка выборки.
По условию задачи 
Расчет ошибки доли при типической выборке при пропорциональном размещении единиц определяется по формуле:
где 
— среднегрупповая выборочная дисперсия доли рассчитывается по формуле:
,
где 
— доля брака для каждого станка.
;
;
.
.
При вероятности P(t) = 0,683 t =1.
или 4%.
Доверительные интервалы:
,
.
Таким образом, доля процент брака для всей партии продукции находится в интервале от 1,6% до 2,4%, что можно утверждать с вероятностью 0,683 или в 683 случаев из 1000.
2. По второму заданию известна допустимая ошибка = 0,5% или 0,005, 
=0,004 (по первому заданию).
;
Отсюда 
, 
.
Величине t = 1,25 соответствует вероятность 0,7887.
Задача 9
При контрольной проверке качества яблок проведена 10%-ная серийная выборка. Из партии, содержащей 50 ящиков яблок (вес ящиков одинаков), методом механического отбора взято 5 ящиков. В результате сплошного обследования находящихся в ящике яблок получили данные об удельном весе бракованных яблок. Результаты представлены в таблице:
| Номер ящика, попавшего в выборку | |||||
| Удельный вес бракованной продукции, % | 1,3 | 1,7 | 1,8 | 1,3 | 1,4 |
Требуется с вероятностью 0,954 установить доверительные интервалы удельного веса бракованной продукции для всей партии яблок.
Для установления доверительного интервала, в котором для всей партии поставки находится доля бракованной продукции, используется формула:
.
,
где 
– межсерийная (межгрупповая) выборочная дисперсия доли;
m – число ящиков, попавших в выборку;
М – общее число ящиков.
При вероятности Р = 0,954 t = 2
или 0,015
(при расчете использована простая арифметическая, так как вес ящиков одинаков).
или 0,3%.
Доля находится в пределах:
.
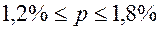Доверительные интервалы удельного веса бракованной продукции для всей партии яблок находятся в интервале от 1,2 до 1,8%, что можно утверждать с вероятностью 0,954.
Задача 10
В цехе проектируется проведение моментных наблюдений для выявления текущих простоев производственного оборудования.
Требуется для организации моментных наблюдений определить необходимое число наблюдений и число обходов, если в цехе имеется 50 единиц предназначенного к работе оборудования. Никаких предварительных данных о доле простоев в сменном фонде не имеется. Ошибка наблюдения не должна превышать 5% и быть гарантирована с вероятностью 0,954.
Решение.
Необходимая численность моментов наблюдения определяется по формуле:
По условию задачи:
t = 2 (так как вероятность Р = 0,954);
w–доля простоев по условию не дана, поэтому принимается наибольшая дисперсия альтернативного признака, когда w = 0,5.
= 5%, или 0,05,
тогда необходимая численность равна:
.
Число обходов (т.е. число записей о каждой единице оборудования) определяется путем деления числа наблюдений на число единиц оборудования:
.
Задача 11
Согласно условию вышерассмотренного примера, из совокупности отобрано 20 предприятий из 100 или 20%. При этом предельная ошибка равна 3,63. Если из генеральной совокупности отобрать 5% предприятий (5 из 100), то какой будет величина средней и предельной ошибки?
Рассчитаем величину средней и предельной ошибки:
.
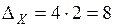
Следовательно, ошибка увеличилась более, чем в 2 раза (8:3,63).
Решение типовых задач по теме
