1. Теорема о нуле непрерывной функции.
Если функция непрерывна на некотором отрезке и на концах этого отрезка принимает значения противоположных знаков, то существует точка, в которой значение функции равно нулю. Формально: пусть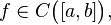 
и 
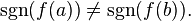Тогда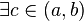 
такое, что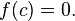 
2. В частности любой многочлен нечётной степени имеет, по меньшей мере, один нуль.
Иногда теорему о нуле непрерывной функции называют первой теоремой Больцано-Коши, а теорему о промежуточном значении - второй теоремой соответственно. Хотя на самом деле эти теоремы эквивалентны.
18 Первая и вторая теорема вейерштрасса.
Теорема (первая теорема Вейерштрасса)
Если функция непрерывна на сегменте, то она ограничена на нем.
Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [ a; b ]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x 0∈[ a; b ].
Пусть f не ограничена на сегменте [ a; b ], например, сверху, тогда для всякого натурального n ∈ N найдется точка xn ∈[ a; b ], что f (xn)> n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn)точек сегмента [ a; b ], для которых выполнено свойство f (x 1)>1, f (x 2)>2, f (x 3)>3,..., f (xn)> n...
Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk), которая сходится к точке x 0∈[ a; b ]: lim k →∞ xnk = x 0 (1)
Рассмотрим соответствующую последовательность (f (xnk)). С одной стороны f (xnk)> nk и поэтому lim k →∞ f (xnk)=+∞ (2),
С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметьlim k →∞ f (xnk)= f (x 0) (3)
Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.
Замечание 1
Таким образом, если f непрерывна на [ a; b ], то ее множество значений ограничено и поэтому существует конечные верхняя и нижняя грань функции.
c =inf x ∈[ a; b ] f (x), d =sup x ∈[ a; b ] f (x), но открыт вопрос о достижении
функции своих граней.
Замечание 2
Если слово сегмент в условии теоремы заменить словом интервал или полуинтервал, то теорема может и нарушиться. Пример, y = tgx, tgx ∈ C ((−2π;2π)), но функция не ограничена на этом интервале.
Теорема (вторая теорема Вейерштрасса)
Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения).
Доказательство: Пусть f (x)∈ C ([ a; b ]), c =inf x ∈[ a; b ] f (x), d =sup x ∈[ a; b ] f (x). По первой
теореме Вейерштрасса c, d ∈ R. Докажем, что f достигает на [ a; b ] своих граней, т.е. найдутся такие точки x 1, x 2∈[ a; b ], что f (x 1)= c, f (x 2)= d.
Докажем, например, существование точки x 2.
По определению верхней грани имеем (∀ x ∈[ a; b ])(f (x)= d). Предположим противное, т.е. точки x 2, в которой f (x 2)= d на [ a; b ], тогда на [ a; b ] выполняется условие f (x)< d или d − f (x)>0. Далее введем вспомогательную функцию ϕ(x)=1 d − f (x). ϕ(x) на [ a; b ] положительна и непрерывна (как отношение двух непрерывных на [ a; b ] функций и d − f (x)/=0), поэтому по первой Т. Вейерштрасса ϕ(x) на [ a; b ]ограничена.
Это означает, что при некотором М>0 (∀ x ∈[ a; b ])(0<1 d − f (x)≤ M), отсюда имеем f (x)≤ d −1 M < d.
Полученное неравенство противоречит тому, что d является верхней гранью функции f (x) на [ a; b ], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x 2 такой, что f (x 2)= d.
Аналогично доказывается существование точки x 1∈[ a; b ], такой что f (x 1)= c.
Следствие
Если f непрерывна и непостоянна на [ a; b ], то образ этого отрезка [ a; b ] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок.
Доказательство: В самом деле образом отрезка [ a; b ] при отображении f будет отрезок [с; d ], где c =inf[ a; b ] f (x)=min[ a; b ] f (x), а d =sup[ a; b ] f (x)=max[ a; b ] f (x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.
19 Производная функции в точке. Геометрический смысл производной.
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной —интегрирование.
Определение
Пусть в некоторой окрестности точки 
определена функция 
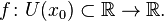Производной функции называется такое число 
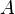, что функцию в окрестности 
можно представить в виде
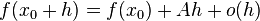
если 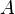существует.
