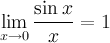
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Следствия из первого замечательного предела
1° 
2° 
3°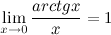 
4°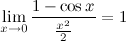 
Второй замечательный предел:
или 
Следствия
1. 
2. 
3. 
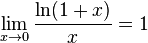
4. 
5. 
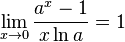для 
, 
6. 
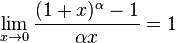
13 Эквивалентные функции. Теорема о вычислении пределов для эквивалентных функций.
Определение:
Если 
в которой определены 
и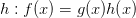 
,
причём 
и 
– эквивалентные при 
и пишут 
Понятие эквивалентные обычно используют, когда f и g – бесконечно малые илибесконечно большие при
Критерий:
Для того, чтобы две бесконечно малые 
и 
были эквивалентны, необходимо и достаточно, чтобы было 
Положив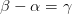 
, будем иметь 
Отсюда сразу и вытекает наше утверждение. Действительно, если 
, то 
, то есть 
есть бесконечно малая высшего порядка, чем и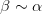 
. Обратно, если дано, ч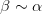то , то , а тогда .
С помощью этого критерия, например, видно, что при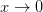 
бесконечно малая 
эквивалентна 
, а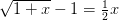 
.
Доказанное свойство эквивалентных бесконечно малых приводит к использованию их при раскрытии неопределённости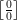 
. Т.е. при разыскании предела отношения двух бесконечно малых 
. Каждая из них при этом может быть заменена, без влияния на предел, любой эквивалентной ей бесконечно малой
14 Непрерывность функции в точке. Различные определения непрерывной функции.
Основные понятия и определения
Определение
Функция 
называется непрерывной в точке 
, если:
1. функция определена в точке и ее окрестности;
2. существует конечный предел функции в точке ;
3. это предел равен значению функции в точке , т.е. 
Замечание
При нахождении предела функции 
, которая является непрерывной, можно переходить к пределу под знаком функции, то есть
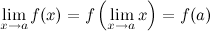
Пример
Задание. Вычислить предел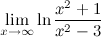 
Решение. 
Ответ. 
Если функции и 
непрерывны в точке , то функции 
, 
, 
также непрерывны в точке ..
Пусть функция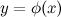 
непрерывна в точке , а функция 
непрерывна в точке 
. Тогда композиция функций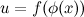 
непрерывна в точке .
Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.
15 Локальные свойства непрерывных функций.
Локальными называют такие свойства функций, которые определяются поведением функции в сколь угодно малой окрестности точки области определения.
1 Теорема – если y=f(x) непрерывна в точкеx0,то она обязательно ограничена в какой т окрестности этой точки.
2 Теорема – если y=f(x)непрерывна в точке x0и y(x0) ≠0,то некоторой окрестност этой точки x0все значения ф-ии либо + либо -!!!
3. Теорема – f(x) + g(x) –если эти 2 функции непрерывны в точке x0,значит в этой точке непрерывна их сумма(разность, произведение и т.д)
4 Теорема – если -U=U(x) имеет предел в точке x0 равный A, то ф-ия y=f(U(x))непрерывна. Lim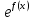 
= 
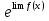
5 Теорема (непрерывность сложной ф-ии) – если U=U(x)непрерывна в точке x0,а y=f(U)непрерывна в точке U0,тогда тогда сложная ф-ия y=f(U(x))также будет непрерывна в точке x0.
16 Точки разрыва функции и их классификация.
Определение точки разрыва
Определение
Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
1. функция определена в точке и ее окрестности;
2. существует конечный предел функции в точке ;
3. это предел равен значению функции в точке , т.е.
называется точкой разрыва функции.
Пример
Функция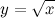 
не определена в точке 
, а значит, эта точка является точкой разрыва указанной функции.
