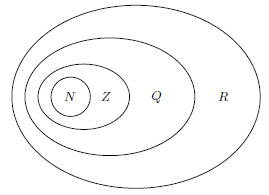
Основные числовые множества
| N | {1,2,3,...,n} Множество всех натуральных чисел |
| Z | {0, ±1, ±2, ±3,...} Множество целых чисел.Множество целых чисел включает в себя множество натуральных. |
| Q | Множество рациональных чисел.
Кроме целых чисел имеются ещё и дроби. Дробь — это выражение вида  , где p — целое число, q — натуральное. Десятичные дроби также можно записать в виде . Например: 0,25 = 25/100 = 1/4. Целые числа также можно записать в виде . Например, в виде дроби со знаменателем "один": 2 = 2/1.
Таким образом любое рациональное число можно записать десятичной дробью — конечно или бесконечной периодической.
|
| R | Множество всех вещественных чисел.
Иррациональные числа — это бесконечные непериодические дроби. К ним относятся:
§ число  — отношение длины окружности к её диаметру;
§ число  — названное в честь Эйлера и др.;
Вместе два множества (рациональных и иррациональных чисел) — образуют множество действительных (или вещественных) чисел.
|
Операции над множествами
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Свойства операций над множествами
Свойства перестановочности
A ∪ B = B ∪ A
A ∩ B = B ∩ A
Сочетательное свойство
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
2 Понятие функции. Способы задания функции. Элементарные функции.
Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут 
, при этом x называют аргументом функции, y называют значением функции.
- Способы задания функции
Задать функцию означает установить правило (закон) с помощью которого по данным значениям независимой переменной находим соответствующие им значения функции. Рассмотрим различные способы задания функции.
- Табличный способ. При этом способе в определенном порядке выписываются ряд значений независимой переменной
и соответствующие им значения функции 
. Таковы, например, таблицы логарифмов, таблицы значений тригонометрических функций и т.д. Табличный способ очень распространен в технике, естествознании и т.п. Численные результаты последовательных наблюдений какого-либо процесса или явления выписываются в виде таблицы. Например, результаты измерений температуры воздуха на метеорологической станции за один день оформляются так:
| t, ч | ||||||||||
| Т, °С | -1 | -2 | -2,5 | -2 | -0,5 | 3,5 |
Эта запись определяет температуру Т как функцию от времени t:T=f(t). Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения функции сразу, без дополнительных изменений или вычислений. Недостатки: определяет функцию не полностью, а лишь для некоторых значений аргумента; не дает наглядного изображения характера изменения функции с изменением аргумента.
2. Графический способ. Графиком функцииy=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Это может быть некоторая кривая, в частности прямая, множество точек на плоскости.
Преимущество – наглядность, недостаток – нет возможности точно определить значения аргумента. В технике и физике часто он является единственно доступным способом задания функции, например, при пользовании самопишущими приборами, которые автоматически записывают изменение одной величины относительно другой (барограф, термограф и др.).
3. Аналитический способ. По этому способу функция задается аналитически, с помощью формулы. Такой способ дает возможность по каждому численному значению аргумента х найти соответствующее ему численное значение функции у точно или с некоторой точностью.
При аналитическом способе функция может быть задана и несколькими разными формулами. Например, функция
задана в области определения [- 
, 15] с помощью трех формул.
Если зависимость между х и у задана формулой, разрешенной относительно у, т.е. имеет вид у = f(x), то говорят, что функция от х задана в явном виде, например, 
. Если же значения х и у связаны некоторым уравнением видаF(x,y) = 0, т.е. формула не разрешена относительно у, то говорят, что функция задана неявно. Например, 
. Заметим, что не всякую неявную функцию можно представить в виде у =f(x), наоборот, любую явную функцию всегда можно представить в виде неявной: 
. Еще одна разновидность аналитического задания функции – параметрическое, когда аргумент х и функция у являются функциями третьей величины – параметраt: 
, где 
, Т – некоторый промежуток. Такой способ широко применяется в механике, в геометрии.
Аналитический способ является самым распространенным способом задания функции. Компактность, возможность применения к данной функции аппарата математического анализа, возможность вычисления значений функции при любых значениях аргумента – его основные преимущества.
4. Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами. Например, функция Е(х) – целая часть числа х, функция Дирихле, функция Римана,n!,r(n) – число делителей натурального числаn.
5. Полуграфический способ. Здесь значения функции представляются в виде отрезков, а значения аргумента – в виде чисел, проставленных на концах отрезков, указывающих значения функции. Так, например, в термометре есть шкала с равными делениями, у которых проставлены числа. Эти числа являются значениями аргумента (температуры). Они стоят на том месте, которое определяет графическое удлинение столбца ртути (значения функции) в связи с ее объемным расширением в результате температурных изменений.
3 Аксиоматическое определение множества действительных чисел.
О п р е д е л е н и е. Совокупность элементов x, y, z, …, состоящая более чем из одного элемента, называется множеством R действительных чисел, если для этих объектов установлены следующие операции и отношения:
I. Для 
определено единственное число a + b, называемое суммой двух действительных чисел, так что выполняются условия:
1) a + b = b + a – свойство коммутативности операции сложения;
2) a + b + c =(a + b) + c — свойство ассоциативности операции сложения;
3) $ число ноль 
такое, что a + 0= a для 
0 – это нейтральный элемент операции сложения;
4) для $ противоположное число 
такое, что a + (–a)= 0;
5) число a + (–b) = a – b называется разностью чисел a и b.
II. Для 
определено единственное число a·b (или ab), называемое произведением двух действительных чисел, так что выполняются условия:
1) a·b = b·a – свойство коммутативности операции умножения;
2) a·b·c =(a·b) ·c – свойство ассоциативности операции умножения;
3) $ число единица 
такое, что a· 1= a для
1 – это нейтральный элемент операции умножения;
4) для 
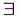единственное обратное число 
такое, что 
;
5) число 
(или a: b) называется частным от деления числа a на число b.
III. Имеет место свойство дистрибутивности произведения относительно суммы:
(a + b) ·c = a·c + b·c для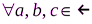 
.
IV. Упорядоченность множества действительных чисел.
Для имеет место одно и только одно отношение порядка:
a < b или a = b или a > b. При этом выполняются условия:
1) если a < b и b < c, то a < c — транзитивность;
2) если a < b, то a + c < b + c для 
;
3) если a < b и c > 0, то a · c < b · c.
Как следствие этих условий получается свойство плотности множества действительных чисел:
Для и a < b $ число 
.
w 
такое, что a < c < b v
Отношения порядка называются неравенствами или сравнениями действительных чисел.
Нестрогие неравенства: 
V. Непрерывность множества действительных чисел:
Для " непустых множеств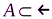 
и 
, у которых для 
и 
выполняется неравенство 
, существует такое число 
, что выполняется соотношение 
для и для (рис. 12).
4 Аксиома полноты. Лемма о вложенных отрезках.
Аксиома непрерывности (полноты). Каковы бы ни были непустые множества 
и 
, такие что для любых двух элементов 
и 
выполняется неравенство 
, существует такое действительное число 
, что для всех и имеет место соотношение
Геометрически, если трактовать действительные числа как точки на прямой, данное утверждение представляется очевидным. Если два множества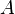 
и 
таковы, что на числовой прямой все элементы одного из них лежат левее всех элементов второго, то найдется число , разделяющее эти два множества, то есть лежащее правее всех элементов 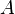(кроме, возможно, самого ) и левее всех элементов (та же оговорка).
Здесь следует отметить, что несмотря на «очевидность» данного свойства, для рациональных чисел оно не всегда выполняется. Для примера, рассмотрим два множества:
Легко видеть, что для любых элементов и выполняется неравенство 
. Однако рационального числа , разделяющего эти два множества, не существует. В самом деле, этим числом может быть только 
, но оно не является рациональным.
Лемма о вложенных отрезках
Формулировка
Для всякой системы вложенных отрезков
существует хотя бы одна точка 
, принадлежащая всем отрезкам данной системы.
Если, кроме того, длина отрезков системы стремится к нулю:
то — единственная общая точка всех отрезков данной системы.
Замечание
Отрезки в формулировке теоремы нельзя заменить на открытые интервалы. Например,
Доказательство
1) Существование общей точки. Множество левых концов отрезков 
лежит на числовой прямой левее множества правых концов отрезков 
, поскольку
В силу аксиомы непрерывности, существует точка , разделяющая эти два множества, то есть
в частности
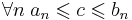
Последнее неравенство означает, что — общая точка всех отрезков данной системы.
2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки и 
, принадлежащие всем отрезкам системы:
Тогда для всех номеров 
выполняются неравенства:
В силу условия стремления к нулю длин отрезков для любого 
для всех номеров , начиная с некоторого будет выполняться неравенство
Взяв в этом неравенстве 
, получим
Противоречие. Лемма доказана полностью.
5 Последовательность. Бесконечно малые и бесконечно большие последовательности.
Числовая последовательность — это последовательность элементов числового пространства.
Последовательность 
называется бесконечно малой последовательностью (б.м.п.), если для любого 
существует номер 
такой, что для любого 
выполняется неравенство: 
Последовательность называется бесконечно большой (б.б.п.), если для любого 
существует номер такой, что для любого выполняется неравенство: 
6 Свойства бесконечно малых последовательностей.
Основные свойства б.м. и б.б. последовательностей
1° Сумма б.м. последовательностей есть б.м.п.
2° Произведение ограниченной последовательности и б.м. есть б.м.п.
3° Если - б.м.п., то - ограниченная последовательность.
4° Произведение б.м.п. есть последовательность б.м.
5° Если - б.м.п. и 
, то 
, т.е. 
6° Если - б.м.п. и 
, то последовательность 
- б.б.п.
7° Если - б.б.п., то 
и последовательность - б.м.п.
7 Сходящиеся последовательности. Предел сходящейся последовательности. Теорема об ограниченности сходящейся последовательности.
Определение: Последовательность {xn} называется сходящейся, если существует такое число а, что последовательность {xn-а} является бесконечно малой. При этом число а называется пределом последовательности {xn}.
В соответствии с этим определением всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число ноль.
