Объяснение нового материала
Задание 1 (с. 32)
Можно показать движение двух объектов с помощью модели, которая двигается. Велосипедист догоняет пешехода, расстояние между велосипедистом и пешеходом уменьшается, они сближаются. Скорость сближения при таком движении равна разности скоростей объектов, которые двигаются.
12-5 = 7 (км/ч) — скорость сближения (догоняет велосипедист пешехода за 1 ч; уменьшается расстояние между велосипедистом и пешеходом за 1 ч);
7·2 = 14 (км) — на столько уменьшится расстояние между велосипедистом и пешеходом за 2 ч;
7·3 = 21 (км) — на столько уменьшится расстояние между велосипедистом и пешеходом за 3 ч.
Закрепление изученного материала
Задание 3 (с. 32)
Ответ: 14 л и 11 л.
Задание 8 (с. 33)
9251; 546; 3052; 1500.
Задание 9 (с. 33)
8138 · 2 = 16276
821 · 9 = 7389
1854 · 5 = 9270
5254 · 7 = 36778
10000 – 749 = 9251
Подведение итогов урока
7. Домашнее задание: № 10, № 11 (ст. 3, 4), стр. 33
МАТЕМАТИКА
Тема: Решение задач на движение в одном направлении
Цели: показать приемы поиска решения задач на движение в одном направлении; закрепить алгоритм умножения многозначного числа на однозначное.
Организационный момент
2. Устный счёт
В воротах этого лабиринта расставлены сомножители. Пройдите четверо ворот и с их помощью наберите произведение, равное 1 000
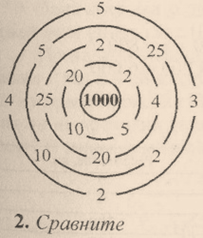
Сравните:
Ответ: 5 • 5 • 4 • 10
2•5 • 20 • 5
2•10•25•2
2•2•25•10
2•25•2•10
4•5•25•20
½ от 400 * ½ от 600
½ от 500 * 1/3 от 900
½ от 700 * ½ от 1000
1/5 от 2000 * 1/6 от 1800
Задание 4 (с. 35)
Задание 2 (с. 34)
Ученики вспоминают правило: чтобы определить количество десятков в числе, надо справа закрыть одну цифру, чтобы определить количество сотен — нужно закрыть две цифры.
Задание 5* (с. 35)
Ученики должны догадаться: чтобы число делилось на 2 и на 3, нужно, чтобы оно делилось на 6. Среди чисел 1, 2, 3, 4,..., 48, 49, 50 делятся на 6 числа 6, 12, 18, 24, 30, 36, 42, 48 — всего 8 чисел.
Решите задачи
• Крейсер проплыл 80 км со скоростью 40 км/ч. Сколько километров он проплыл бы за это время, двигаясь со скоростью 90 км/ч?
• Участок земли имеет форму прямоугольника, длина которого 60 м, а ширина — 40 м. Какой длины забор окружает этот участок? Какова площадь участка?
• Один литр подсолнечного масла весит 920 г. Вычислите массу 1/4 л подсолнечного масла.
Задание 9 (с. 35)
Ответ: 7 груш и 13 яблок.
Сообщение темы и целей урока
Объяснение нового материала
Задание 1 (с. 34)
Сначала анализируется рисунок: поезда двигаются в одном направлении; второй поезд едет с большей скоростью, чем первый; расстояние между поездами уменьшается (сокращается), они сближаются. Может ли второй поезд догнать первый? (Может, потому что он едет быстрее, чем первый.)
Дальше анализируется таблица. Когда второй поезд стал двигаться, первый прошел уже 120 км; расстояние между поездами было первоначально 120 км. Потом расстояние стало сокращаться: 120 км, 90 км, 60 км, 30 км, 0 — за каждый час расстояние сокращается на 30 км. Через 4 ч после выезда второй поезд догонит первый; расстояние между ними будет равно 0. За это время поезда отдалятся от города на 360 км.
После этого оформляется решение:
1) 90-60 = 30 (км/ч) — скорость сближения поездов;
2) 120: 30 = 4 (ч) — понадобится, чтобы второй поезд догнал первый;
3) 90 • 4 = 360 (км) или 60 • 6 = 360 (км) расстояние от города.






