Выходного напряжения
Формулу переходной характеристики можно получить операторным методом [1 с.294–320]
Переходной характеристикой цепи h(t) называется отношение отклика цепи, например, выходного напряжения U2(t) на ступенчатое воздействие, например, входное напряжение U1(t)=U01(t) к величине воздействия U0при нулевых начальных условиях [1,с.315-316]

Численно переходная характеристика равна отклику цепи U2(t), если амплитуда воздействия равна единице U0 = 1.
Операторное изображение отклика U2(p) при заданном операторном воздействии U1(р) определяют с помощью операторной передаточной функции KU(p)
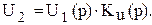
Операторное изображение ступенчатой единичной функции равно U1(р) = =1/р. Следовательно, операторное изображение отклика, т.е. изображение переходной характеристики h(p) определяется выражением

Операторную передаточную функцию KU(р) можно получить из комплексной KU(jω) путем замены jω на p.
В рассматриваемом примере операторное изображение выходного напряжения U77 равно
 (12)
(12)
Операторная функция цепи, как правило, представляет собой правильную несократимую дробную рациональную функцию с вещественными коэффициентами и простыми полюсами. Эта функция может быть единственным образом разложена на сумму простых дробей

где А1, А2,…Ak –коэффициенты, значения которых находят в ходе разложения функции на простые дроби; p*1, р*2,...р*k - полюсы функции U2(p).
Для нахождения оригинала переходной характеристики можно воспользоваться таблицами обратного преобразования Лапласа [1, Приложение 1] отдельно для каждого слагаемого в сумме простых дробей. Оригинал переходной характеристики можно найти также другим способом, известным в теории электрических цепей под названием теорема разложения [1,с.296].
Теорема разложения
Пусть изображение функции цепи задано в виде дроби U2(p)=M(p)/N(p), причем степень полинома числителя М(р) ниже степени полинома знаменателя N(p). Для перехода от изображения U2(p) к оригиналу U2(t) можно воспользоваться теоремой разложения. При этом возможно два случая; а) все полюсы функции U2(p) простые; б) некоторые из них или все полюсы кратные.
А) Случай простых полюсов
Оригинал определяется по следующей формуле:

Частный случай: один из полюсов равен нулю –р* = 0.
При этом изображение функции можно представить в виде
U2(p) = M(p)/N(p) = M(p)/p·Q(p).
Обозначим полюс, равный нулю, через р0, а полюсы уравнения Q(p) = 0 через p1, p2,...pn. Тогда формула разложения имеет следующий вид:

Если среди полюсов p1, p2,... pn есть пара комплексно–сопряженных, например, p1,2 =–s ± jw, то в оригинале двум членах суммы с этими полюсами соответствует временная функций в виде затухающего гармонического колебания:

где







