Формулы амплитудно-частотной и фазо-частотной характеристик (АЧХиФЧХ) можно получить с помощью дробно-рациональной операторной функции КU(р). Для этого нужно заменить операторную переменную р на мнимую частоту jω (p=jω). Получится комплексная функция частоты KU(jω). Необходимо выделить действительную и мнимуючасти в числителе и знаменателе, а затем преобразовать комплексную функцию частоты KU(jω) в показательную форму:
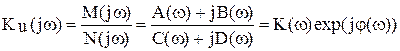 . (7)
. (7)
Формула АЧХ представляет собой зависимость модуля (амплитуды) комплексной функции от частоты:
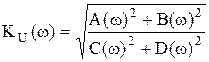 . (8)
. (8)
Для нашего примера (см. ф.(6))
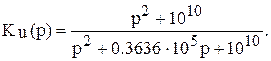
При p=jω
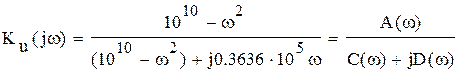 . (9)
. (9)
Учитывая (8), и что
A(ω)=(1010–ω 2) B(ω)=0, C(ω)=(1010 –ω 2) D(ω)=0.3636·105ω,
получим выражение (10) АЧХ
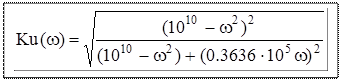
(10)
Формула ФЧХ выражает зависимость аргумента (фазового угла) комплексной функции KU(jω) от частоты:
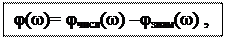
(11)
где φ числ(ω) – аргумент комплексного числителяКU(jω),
φ знам(ω) – аргумент комплексного знаменателяКU(jω).
При записи формул для φ числ(ω) и φ знам(ω) следует учитывать, что фазовый угол произвольного комплексного числа M(jω)=А(ω)+jB(ω) вычисляется различным образом в зависимости от положения комплексного числа на комплексной плоскости (см. таблицу 1).
Отсюда следует, что выражение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива в некотором своем диапазоне частот. Граничные частоты диапазонов можно оценить приближенно, так как в точках, близких к биссектрисам координатных квадрантов, можно пользоваться формулами обеих соседних областей.
Для нашего примера действительные A(ω) и C(ω) и мнимая D(ω) части числителя и знаменателя коэффициента передачи (9) зависят от частоты и не только меняют свое значение, но и меняют знак. А это значит, что комплексные числа числителя и знаменателя меняют свое положение на комплексной плоскости. Это обстоятельство требует анализа аргументов числителя φчисл(ω) и знаменателя φзнам(ω) при изменении частоты от нуля до бесконечности.
1). Анализ числителя для определения его аргумента.
Действительная часть числителя равна A(ω)=1010–ω2. Если 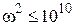 , т.е.
, т.е. 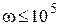 , числитель представляет собой действительное и положительное число – A(ω) ≥ 0. Поэтому φ числ(ω)=0 при
, числитель представляет собой действительное и положительное число – A(ω) ≥ 0. Поэтому φ числ(ω)=0 при 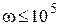 .
.
При 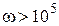 , A(ω) < 0. Поэтому φ числ(ω)=
, A(ω) < 0. Поэтому φ числ(ω)= 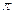 .
.
2). Анализ знаменателя.
Действительная часть знаменателя равна действительной части числителя C(ω)=A(ω)=1010–ω2 и изменяется с изменением частоты также, как и числитель. Мнимая часть знаменателя D(ω)=0.3636·105ω прямо пропорциональна частоте ω и положительная D(ω)> 0 при ω > 0.
Таблица 1
| №пп | Область компл. пл. | Условия M(jω)=A(ω)+jB(ω) | Формула φ (ω)= |
 1) 1)
| A(ω) > 0. úB(ω)ú £ A(ω) | 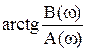 . .
| |
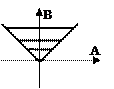 2) 2)
| B(ω) > 0. úA(ω)ú £ B(ω) | 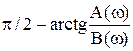 . .
| |
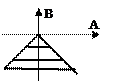 3) 3)
| B(ω)£ 0. úA(ω)ú £ –B(ω) | 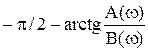 . .
| |
 4) 4)
| A(ω) < 0. B(ω)> 0. úB(ω)ú £–A(ω) | 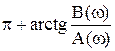 . .
| |
 5) 5)
| A(ω) < 0. B(ω) < 0. úB(ω)ú £–A(ω) | 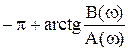 . .
|
При 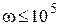 точка, отображающая знаменатель, находится в первом квадранте комплексной плоскости, причем при ω>0.8346 105 она пересекает биссектрису первого квадранта. Поэтому в диапазоне 0< ω<0.8346·105 при вычислении фазового угла знаменателя нужно использовать формулу 1 из таблицы 1:
точка, отображающая знаменатель, находится в первом квадранте комплексной плоскости, причем при ω>0.8346 105 она пересекает биссектрису первого квадранта. Поэтому в диапазоне 0< ω<0.8346·105 при вычислении фазового угла знаменателя нужно использовать формулу 1 из таблицы 1: 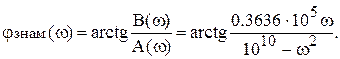
При 0.8346·105 <ω 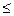 1.1982·105 отображающая точка находится в области 2 таблицы 1. Поэтому
1.1982·105 отображающая точка находится в области 2 таблицы 1. Поэтому 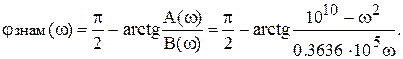
При ω >1.1982·105 точка переходит в область 4 таблицы 1.
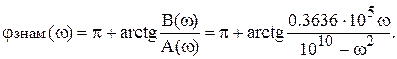
Таким образом, ФЧХ коэффициента передачи в нашем примере будет описываться различными формулами для четырех частотных областей.
 |






