В.А Михайлов, Э И. Султанов
РАСЧЕТ ЧАСТОТНЫХ И ПЕРЕХОДНЫХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ АКТИВНЫХ ЦЕПЕЙ
Методическое пособие по курсовой работе
Казань 2001
УДК 621. 372 (075)
Расчет частотных и переходных характеристик линейных активных цепей: методическое пособие по курсовой работе. В.А. Михайлов, Э.И. Султанов. Казан. гос. техн. ун-т. Казань, 2001, 27 с.
Методическое пособие по курсовой работе по курсу “Основы теории цепей” для студентов 2-го курса направления 552500 “Радиотехника’’, специальностей 2007, 2010, 2012. Даются краткие теоретические сведения и методические советы. Приведен пример выполнения курсовой работы.
Табл. 4. Ил.7. Библиогр: 3 назв.
Рецензент: канд.техн. наук, доц. Е.Ф.Базлов (кафедра теоретической радиотехники и электроники КГТУ им.А.Н.Туполева).
Оглавление
Предисловие..................................4
1. Вывод формулы операторной функции активной цепи......... 5
2. Вычисление особых точек. Построение полюсно - нулевой карты... 7
3. Вывод формул частотных характеристик..................9
4. Расчет и построение частотных характеристик............. 11
5. Вывод формулы переходной характеристики.............. 14
6. Расчет и построение переходной характеристики............ 17
7. Выводы................................... 18
8. Рекомендации по оформлению курсовой работы.............19
ПРИЛОЖЕНИЯ
Приложение 1. Частотные характеристики, построенные в разных масштабах по осям..................................21
Приложение 2. Образец титульного листа курсовой работы........22
Приложение 3. Пакет контролирующих и вычислительных программ
для курсовой работы по Основам теории цепей.................. 23
Предисловие
Курсовая работа по курсу “Основы теории цепей” ставит целью закрепить навыки аналитического расчета входных и передаточных функций, а также численного расчета частотных и переходных характеристик линейных активных цепей на ЭВМ. Работа выполняется студентами в период изучения всего курса.
Работа посвящена численному расчету и исследованию частотных и переходных характеристик линейного активного четырехполюсника. При выполнении курсовой работы студенты должны закрепить основные понятия теории цепей: электрическая цепь, четырехполюсник, схема замещения операционного усилителя, амплитудно-частотные, фазо-частотные и переходные характеристики и т. д. Применить на практике методы анализа активных электрических цепей и расчета характеристик с помощью ЭВМ.
Каждому студенту на первой консультации выдается индивидуальное задание: вид исследуемой цепи, значение параметров элементов, вид рассчитываемых параметров и характеристик.
В пособии все теоретические вопросы применены при решении примера, подобного по содержанию заданию по курсовой работе.
Пример:
Курсовая работа по ОТЦ. Вариант 402.
Исследовать частотные и переходные характеристики линейного активного четырехполюсника – электрического фильтра (принципиальная схема цепи изображена на рис.1).
1. Вывести операторную функцию коэффициента передачи по напряжению КU(р);
2. Рассчитать и построить карту особых точек (нулей и полюсов) функции;
3. Рассчитать и построить частотные характеристики KU(jω);
4. Рассчитать и построить переходную характеристику Uвых(t ).
Параметры элементов: R1=R2=R4=0.5 kOм, R3=0,5 kOм, R5=10 кОм, С1=С2=10 нФ, C3=20 нФ.
 |
Вывод формул операторных функций
Активной линейной цепи
Операторные функции цепи могут быть получены по операторной схеме замещения цепи, которая получается из исходной схемы путем замены всех элементов их операторными сопротивлениями [1,с. 297–302, 3, с.251–255]. Если исходная схема содержит активные элементы - электронные лампы, транзисторы, операционные усилители и т. д., то их нужно заменить эквивалентными схемами [1, с.30–32].
Любая операторная функция цепи представляет собой отношение операторного изображения отклика Y(p)↔y(t) к операторному изображению внешнего воздействия Х(р)↔х(t) при нулевых начальных условиях для реактивных эле м ентов цепи iL(–0)=0, uC(–0)=0:
(1)
Для определения операторного отклика цепи на заданное операторное воздействие можно воспользоваться любым известным методом расчета цепей, например, методом узловых напряжений или методом контурных токов [1, с. 203–208; 3, с. 9–11].
 |
В качестве конкретного примера приведем вывод формулы операторного коэффициента передачи по напряжению КU(р) фильтра, схема которого представлена на рис. 1 (см. п.1 в примере задания по курсовой работе).
 |
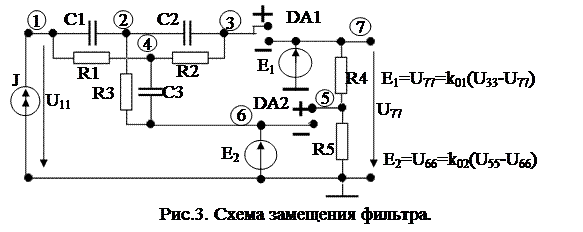Схема фильтра содержит два операционных усилителя DA1 и DA2. Представим их схемами замещения в виде источников ИНУН E1и E2 с бесконечно большим коэффициентом передачи k0 (рис.2). На входе фильтра подключим источник тока J(p ). Пронумеруем узлы схемы цифрами 1–7. Узел, отмеченный знаком «┴», является базисным. Полученная схема замещения фильтра изображена на рис. 3.
Решим задачу методом узловых напряжений. Обозначим напряжения узлов U11, U22,…..U77. К шестому и седьмому узлам подключены зависимые источники напряжения E2=k02(U55–U66) и E1=k01(U33–U77), моделирующие ОУ. Составим уравнения по первому закону Кирхгофа для независимых узлов 1, 2, 3, 4, 5. Для узлов 6 и 7, которые являются зависимыми, используем основные уравнения ОУ:
U66=E2=k02(U55–U66), U77=E1=k01(U33–U77) или
–k02U55+(k02 +1)U66=0, –k01U33+(k01 +1)U77)=0.
Система уравнений может быть записана в матричной форме:
[Y]∙[U]=[J],
где
,
, 
.
Идеальные операционные усилители имеют большие значения коэффициента передачи: k0→ ∞. Предельный переход при стремлении k01 и k02 к
бесконечности позволяет упростить схему уравнений. Уравнения 6 и 7 в строках сводятся к равенствам U33=U77 и U55=U66, что формально сводится к сложению столбцов 3 и 7, 5 и 6, и вычеркиванию строк 6 и 7. Узловые напряжения U33 и U55 исключаем из столбца напряжений. Система уравнений примет следующий вид:
(2)
Для расчета коэффициента передачи по напряжению нужно определить входное U11 и выходное U77 напряжения:
 |
Операторная функция (1) цепи всегда принимает вид дробной рациональной операторной функции
(3)
В нашем примере H(p)=KU(p)=U77(p)/U11(p). После определения U11и U77получим выражение операторного коэффициента передачи по напряжению:
(4)
где a3=(g4+g5)C1C2C3, a2=(g1+g2)(g4+g5)C1C2,
a1=g1g2(g4+g5)(C1+C2), a0=g1g2g3(g4+g5),
b3=(g4+g5)C1C2C3, b2=(g1+g2)(g4+g5)C1C2+(g2(C1+C2)+g3C2)g5C3,
b1=g1g2(g4+g5)(C1+C2)+g3g5((g1+g2)C2+g2C3), b0=g1g2g3(g4+g5).
Подставив численные значения параметров элементов, получим
,
где a3=2.2×10–27 a2=2.2×10–22 a1=2.2×10–17 a0=2.2×10–12
b3=2.2×10–27 b2=3.0×10–22 b1=3.0×10–17 b0=2.2×10–12.
Желательно поделить числитель и знаменатель на коэффициенты, например, числитель на a3, а знаменатель на b3, чтобы уменьшить порядковую часть в экспоненциальной форме записи численных значений. В результате этого преобразования функция умножается на коэффициент K0= a3/b3:
(5)
где K0=1, a3=1, а2=1×105 а1=1×1010 а0=1×1015,
b3=1, b2=1.3636×105, b1=1.3636×1010, b0=1×1015.
Система уравнений (2) и формулы (4) и (5) являются результатом выполнения первого пункта задания курсовой работы.
