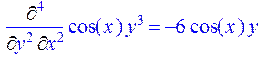· Общие сведения о СКМ Maple
Работа в СКМ Maple организована в диалоговом режиме: вопрос – ответ в отдельном блоке. Блок выделяется слева квадратной скобкой, длина которой зависит от размеров и количества исходных выражений (вопросов) и результатов вычислений (ответов). Строка ввода математических выражений имеет отличительный символ >.
Алфавит языка содержит 26 прописных и строчных латинских букв (от A до Z и от а до z), 10 арабских цифр (0 – 9) и 32 специальных символа. Идентификатор должен быть уникальным, начинаться с буквы и может содержать буквы, цифры и знак подчеркивания. Maple различает прописные и строчные символы.
Выражение задается с помощью функций и операторов, записываемых в командной строке. Результат вычислений (по умолчанию) возвращается в виде математических формул. Ввод выражения завершается символом фиксации конца выражения – точкой с запятой, если ответ выводится в ячейку вывода, или двоеточием, если ответ не выводится.
Выражения формируются из операторов и операндов. Операндами могут быть константы, переменные и значения функций.
В СКМ Maple могут использоваться следующие операторы:
| + - оператор сложения | -> - функциональный оператор | |
| - - оператор вычитания | < - менее чем | |
| * - умножение | > - более чем | |
| / - деление | = - равно | |
| **, ^ - возведение в степень | <= - менее чем и равно | |
| ! – факториал | >= - более чем и равно | |
| . – десятичная точка | <> - неравно | |
| := - оператор присваивания | or – логическое ИЛИ | |
| and – логическое И |
· Функции
Важным понятием СКМ Мaple является понятие функции. Функция возвращает результат некоторого преобразования исходных данных - параметров функции.
Встроенные функции Мaple хранятся в его ядре и пакетах расширений. Дополнительные функции из пакетов расширения должны применяться после объявления загрузки пакета с помощью команды,
with (name),
где name — имя применяемого пакета.
Практически все функции задаются именем и аргументом, в качестве которого может задаваться математическое выражение.
Математические функции ( все они известны):
Sin, cos, tan, sec, csc, cot, arcsin, arcos, arctan.., exp...,sqrt…
ilog10, ilog - целочисленные логарифмы (ilog10(25)=1);
ln, log, log10, sqrt, abs.
Некоторые целочисленные функции:
factorial(n) – альтернатива!;
iquo (a,b) – частное от деления а на b;
irem (a,b ) – остаток от деления а на b;
igcd(a,b ) - наиб. общий делитель;
lcm – наименьшее общее кратное;
Функции с элементами сравнения:
ceil – наименьшее целое >=x;
floor – наибольшее целое <=x;
frac– дробная часть числа х;
trunc – меньшее целое, округленное в направлении к нулю;
round – округленное значение числа;
signum – функция знака (-1, 1);
Функции пользователя в СКМ Мaple могут задаваться следующим образом:
1. Присваивание (с помощью оператора присваивания:=) Пример:
> m:=sqrt(x^2+y^2);
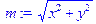
> x:=3: y:=4: m;
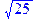
2. C помощью оператора à в фомате:
name:=(x,y,…) à expr;
Вызов функции осуществляется в виде:
name(x,y), где x,y – список формальных параметров.
Пример:
> restart;
> x:=o;y:=0;
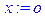
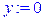
> m:=(x,y)->sqrt(x^2+y^2);
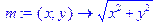
> m(3,4);
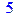
> m(0,1);
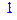
> [x,y];
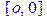
3. C помощью оператора unapply в фомате:
name:= unapply(expr, var1, var2,..);
Пример:
> restart;
> fm:=unapply(sqrt(x^2+y^2),x,y);
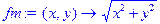
> m:=fm(3.,4);
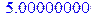
Для оценивания выражения, т.е. представления его в числовом виде существует функция evalf (из группы eval).
Ее формат: evalf(expr, n) – вычисляет expr и возвращает вычисленное значение в форме с плавающей точкой, имеющей n цифр после десятичной точки. Параметр n является необязательным, при его отсутствии n=10.
> evalf(m);
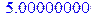
> evalf(m,2);
 m=
m=
Количеством выводимых после десятичной точки цифр можно управлять, задавая значение системной переменной Digits:
> Digits:=3;evalf(m);
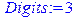
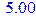
· Типовые средства графики
В само ядро Maple встроено ограниченное число функций графики. Это, прежде всего, функция для построения двумерных графиков plotи функция для построения трехмерных графиков plot3d. Они позволяют строить графики наиболее распространенных типов в различных системах координат, как на плоскости, так и в трехмерном пространстве. Для построения графиков более сложных типов необходимо подключать пакеты расширений Maple.
Для построения двумерных графиков используется команда plot.
Формат:
plot(function, variable_x {,variable_y}{option});
где function – функция, график которой строится;
variable_x– переменная, указывающая область изменения по горизонтали;
variable_y – переменная, указывающая область изменения по вертикали;
option – набор опций, задающий стиль построения графика функции.
При построении графиков функцию можно определять через переменную.
Для двумерной графики можно включать следующие опции:
- numpoints – изменение количества точек графика (по умолчанию=49);
- color – задание цвета кривой графика;
- title – добавление заголовка графика (например, title=”string”);
- coords – выбор системы координат, этот параметр задает 15 типов координатных систем. По умолчанию задана прямоугольная система координат;
- axes – задание типа осей координат (frame - рамка, boxed - прямоугольник, normal - ортогональные, none – без осей);
- thickness – толщина линии графика;
- xtickmarks, ytickmarks – управление числом меток на оси, т.е. задает минимальное число отметок по оси х и у соответственно;
- style – стиль построения графика (line – выводится интерполяционная кривая, point – выводятся точки);
- scalling – масштаб графика (constrained – сжатый, unconstrained - несжатый);
- size – размер шрифта в пунктах;
- symbol – тип точки графика в виде символа (box - прямоугольник, cross - крест, circle - окружность, point – точка, diamond - ромб);
- titlefont – шрифт для заголовка;
- labelfont – шрифт для меток (labels) на осях координат;
- view=[A,B] – определение максимальной и минимальной координат, в пределах которых график будет отображаться на экране, где A=[xmin..xmax], B=[ymin..ymax].
Примеры построения двумерных графиков различных видов
1. Построение графика неявно заданной функции sin(x)/x на интервале -15..15 (см. рис. 1).
> plot(sin(x)/x, x=-15..15,color=red, title="график");

Рис.1. График функции sin(x)/x
2. Построение графика функции sin2(x) определенной c помощью оператора присваивания, на интервале x=-5..5,y=0..0.5, черного цвета в виде совокупности точек (см. рис. 2).
> fun:=sin(x)^2;
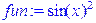
3. Построение графиков трех функций sin(x),sin(x)/x, sin(x3/100) линиями трех цветов и трех типов (см. рис. 3).
> plot([sin(x),sin(x)/x,sin(x^3/100)],x=10..10, color = [black,blue,red],style=[line, line, point]);
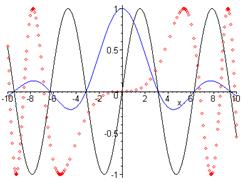
Рис.3. График трех функций
Для построения трехмерных графиков Maple имеет встроенную в ядро функцию plot3d. Она может использоваться в следующих форматах:
plot3d(expr1, x = a..b, y = c..d, p),
plot3d(f, a..b, c..d, p),
plot3d([exprf, exprg, exprh], s = a..b, t = c..d, p),
plot3d([f, g, h], a..b, c..d, p).
Здесь p – параметры, с помощью которых можно в широких пределах управлять видом трехмерных графиков.
Трехмерными называют графики, отображающие функции двух переменных z(x,y). На деле трехмерные графики представляют собой объемные проекты в аксонометрии.
Пример построения трехмерного графика. Построить поверхность h2 в цилиндрической системе координат (см. рис. 4).
> plot3d(h^2,a=-Pi..Pi,h=-5..5, coords=cylindrical, style =patch, color=sin(h));
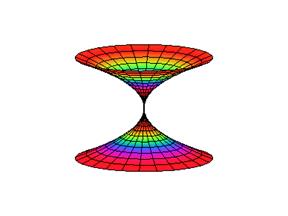
Рис.4. Пример трехмерного графика
· Решение уравнений
Для решения уравнений, неравенств и их систем в СКМ Maple используется функция solve, которая возвращает последовательность решений.
Формат
solve(eqn, var);
где eqn – уравнение, неравенство или процедура;
var – имя переменной.
Уравнение и его решение можно представлять в виде отдельных объектов, отождествленных с определенной переменной.
Пример
> y:=x^2+2*x-3;# задание уравнения через переменную eqn
> rez:=solve(y,x);# решение уравнения и присвоение корней переменной rez.
> x1:= rez [1];# присвоение первого корня переменной х1
> x2:= rez [2];# присвоение второго корня переменной х2
> subs(x=x1, y);# подстановка первого корня в уравнение
> subs(x=x2, y);# подстановка первого корня в уравнение
Если решений нет или функция не может найти решение, то возвращается пустая последовательность NULL. В этом случае целесообразно использовать функцию fsolve, которая возвращает корень уравнения в форме вещественного числа.
Формат
fsolve(eqn, var);
eqn – уравнение, неравенство или процедура;
var – имя переменной.
Пример
> solve(exp(x)+ln(2*x)-4.2*x);
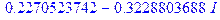
Как видно из результата решения данного уравнения, корень представлен с использованием мнимой единицы, что не дает представления о его числовом значении, поэтому для его решения следует воспользоваться командой fsolve.
> fsolve(exp(x)+ln(2*x)-4.2*x);
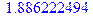
· Решение систем линейных алгебраических уравнений
Системы линейных алгебраических уравнений можно решать также, используя команду solve. Такое решение в силу простоты записи может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств, то есть с использованием фигурных скобок.
Пример
> sys:={3*x1-4*x2-x3=10,6*x1-8*x2-3*x3=19,-x1+x2+x3=-3};
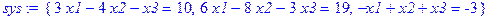
> rez:=solve(sys,{x1,x2,x3});
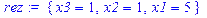
> subs(rez={x1,x2,x3},sys); # подстановка результатов в СЛАУ
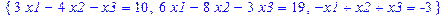
· Вычисление интегралов
Вычисление неопределенного интеграла обычно заключается в нахождении первообразной функции.
Для вычисления неопределенных интегралов Maple представляет следующие функции:
Int(f,x) – отложенного действия
int(f,x) - прямого действия
Для вычисления определенных интегралов Maple представляет следующие функции
Int(f,x=a..b, continuous) – отложенного действия;
int(f,x=a..b, continuous) - прямого действия;
Здесь f – подынтегральная функция,
x – переменная, по которой выполняются вычисления,
аиb –верхний и нижний пределы интегрирования.
continuous – необязательное дополнительное условие.
Для вычисления значения определенного интеграла необходимо использовать функцию evalf:
evalf(int(f, x=a..b)).
Если верхним пределом интегрирования является бесконечность, то в функции int она обозначается словом infinity.
Пример:
> restart;
> Int(sin(x)/x, x=0..1.)=int(sin(x)/x, x=0..1.);
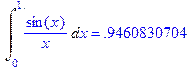
> Int(x*exp(-x),x=0..infinity)=int(x*exp(-x), x = 0..infinity);
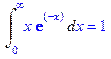
· Вычисление производных
Вычисление производных функций fn(x) =d fn(x)/ d xn – одна из самых распространенных задач мат. анализа. Для ее реализации Maple6 имеет следующие основные функции:
diff(a,x1,x2,…,xn) diff(a,[x1,x2,…,xn])
Diff(a,x1,x2,…, xn) Diff(a,[x1,x2,…,xn])
здесь a– дифференцируемое алгебраическое выражение, в частности функция f(x1, x2,…,xn)ряда переменных, по которым производится дифференцирование.
Функция Diffявляется инертной формой вычисляемой функции diff и может использоваться для естественного вычисления производной в документах.
В простейшей форме diff(f(x),x)вычисляет первую производную функции f(x)по переменной x. При nбольшем 1, вычисления производных выполняются рекурсивно, например diff(diff(f(x),x),y).Или же для вычисления производных высокого порядка можно использовать оператор $.Напримервыражениеdiff(f(x), x$4),вычисляющее производную четвертого порядка по x, эквивалентно по записи diff(f(x),x,x,x,x).
Примеры:
> Diff(a*x^n,x)=diff(a*x^n,x);
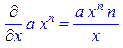
> Diff(sin(x),x)=diff(sin(x),x);

> f(x,y):=cos(x)*y^3;

> Diff(f(x,y),x)=diff(f(x,y),x);
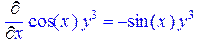
> Diff(f(x,y),x$2,y$2)=diff(f(x,y),x$2,y$2);