В экономике и, следовательно, в эконометрике исследуемые явления и характеризующие их величины — это сложные случайные процессы и случайные величины. Случайные величины 
в процессе анализа представляются состоящими из постоянной и случайной компонент. При этом постоянная составляющая — это математическое ожидание, или среднее арифметическое (среднее) значение исходной случайной величины:
. (1.4)
Если же данные не сгруппированы, то все частоты f равны 1 и получаем формулу простого среднего:
. (1.5)
Среднее случайной компоненты, или остатка, равно нулю. Если бы это оказалось не так, то это ненулевое значение следовало бы включить в среднее значение исходной случайной величины и таким образом все свелось бы к предыдущему.
Мера разброса (вариации) случайной величины, или, что то же, ее распределения, — это дисперсия . Первоначально дисперсия определяется как среднее квадрата разности между самой случайной величиной и средним этой случайной величины:
. (1.6)
В этом выражении коэффициенты f есть не что иное, как веса, или весовые коэффициенты значений величины χ. Это попросту величины, показывающие, сколько раз входят те или иные значения в данное эмпирическое распределение величины χ для дискретных распределений или же в данный интервал (данную группу) для непрерывных распределений.
Часто при расчетах используют выражение для дисперсии в виде разности среднего от квадрата исходной случайной величины и квадрата среднего от нее:
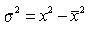. (1.7)
Тогда окончательно для дисперсии исходной случайной величины получаем, что она равна дисперсии остатка, поскольку вся вариация исходной случайной величины равна вариации остатка просто по самому его определению.
В действительности, кроме самых простых и редких случаев, распределение случайной величины и даже основные характеристики изучаемой генеральной совокупности неизвестны. Требуется получить информацию о случайной величине, характеризующей данное явление или процесс, либо, соответственно, генеральной совокупности из результатов наблюдений. Совокупность результатов наблюдений представляет собой выборку из генеральной совокупности, и по этим данным (выборки) с применением подходящей формулы и методов оценивания (прежде всего, метода наименьших квадратов) получают приближенное значение неизвестной характеристики (параметра) исследуемой случайной величины или, в терминах статистики, генеральной совокупности.
Эконометрика использует для изучения различных явлений и процессов признаки, характеризующие эти явления и процессы. Признаки могут быть количественными и атрибутивными , не поддающимися непосредственно количественному измерению. Эконометрика сосредоточена преимущественно на исследовании явлений и процессов, характеризующихся количественными признаками. Тем не менее, она способна исследовать и взаимосвязи между атрибутивными (неколичественными) признаками.
1.5.
