Рассмотрим основные теоретические положения, необходимые для успешного выполнения данного домашнего задания.
В качестве исходных данных в таблицах 1.1. и 1.2. приводятся взятые из справочника следующие величины:
U1Н – номинальное напряжение двигателя, В;
PН – номинальная мощность двигателя, кВт;
nН – номинальная частота вращения ротора, об/мин;
E2Н – э.д.с. заторможенного ротора, В;
I2Н – ток ротора при номинальной нагрузке, А;
λК = MMAX / MН – кратность максимального момента;
ηН – к.п.д., коэффициент полезного действия при номинальной
нагрузке, %;
cosφ1Н – коэффициент мощности при номинальной нагрузке.
Полезной мощностью P2 асинхронного двигателя является механическая мощность, которая определяется через механические параметры так
P2 = M∙Ω = M∙(2π / 60)∙n = 0.105∙M∙n.
Используя номинальные данные P2Н и nН, вычисляем номинальный вращающий момент асинхронного двигателя
MН = 9.55∙P2Н / nН.
Здесь P2Н – в [Вт], nН – в [об/мин], MН – в [Н∙м].
Номинальное скольжение sН определяется по формуле
sН = (n0 – nН) / n0,
где n0 = 60∙f1 / p – частота вращения магнитного поля в АД,
f1 = 50 Гц – частота сети,
p – число пар полюсов двигателя.
n0 может принимать только фиксированные значения в соответствии с таблицей 2.1.
Таблица 2.1.
| p | - | ||||||
| n0 | об/мин |
Зная номинальную частоту вращения nН, определяем из таблицы 2.1. n0 - как ближайшее большее значение к nН. Одновременно определяем число пар полюсов p.
Зная кратность максимального момента относительно номинального λК, определяем MMAX
MMAX = λК∙MН.
Соотношение между моментом M и скольжением s определяется формулой Клосса
M = 2∙MMAX / (s/sКР + sКР/s).
Используя номинальные значения sН и λК, вычисляем величину критического скольжения 
и критическую частоту вращения
nКР = n0∙(1-sКР).

|
Рис. 2.1.
На графике (рис. 2.1.) приведена естественная характеристика n(M) и на ней указаны 4 точки, соответствующие четырем характерным режимам работы асинхронного двигателя:
- точка 1 – соответствует режиму холостого хода;
- точка 2 – соответствует номинальному режиму;
- точка 3 – соответствует критическому режиму;
- точка 4 – соответствует пусковому режиму.
При проведении расчетов в данном задании примем следующее упрощение – момент сопротивления на валу АД не зависит от частоты вращения n, т.е. МС = const.
Участок характеристики n(M) между точками 1 и 2 называется рабочим участком (см. рис. 2.1.).
Участок характеристики n(M) между точками 1 и 3 называется участком устойчивой работы АД.
Участок характеристики n(M) между точками 3 и 4 называется
участком неустойчивой работы АД.
Проводим расчет естественной механической характеристики n(M). Для этого задаемся рядом значений коэффициента скольжения s в диапазоне от 0 до 1 (7-8 значений). Желательно чтобы сюда вошли величины скольжений, соответствующие номинальному sН и критическому sКР режимам.
Для каждого из значений s вычисляем соответствующие величины n и M и записываем их в таблицу 2.2.:
n = n0∙(1-s)
и M = 2∙Mmax / (s/sКР + sКР/s).
Одновременно проводим расчет характеристики n(I2). Определяем активное сопротивление фазы обмотки ротора
 .
.
Здесь Ω0 угловая частота вращения магнитного поля
 .
.
Для каждого из значений s, принятых в таблице 2.2., вычисляем величину тока в обмотке ротора I2

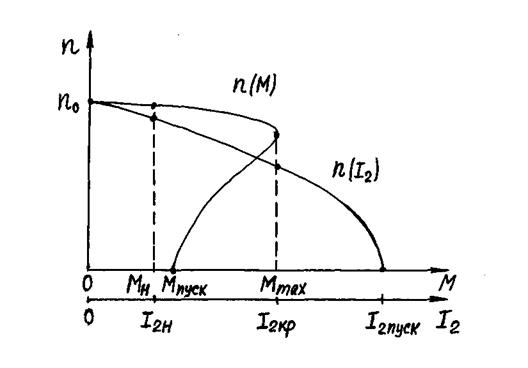
и записываем в таблицу 3.2. Далее на одном графике в общей системе координат строим обе зависимости n(M) и n(I2) (рис. 2.2).
Таблица 2.2.
| s | - | … | sН | … | sКР | … | ||
| n | об/мин | n0 | ||||||
| M | Н∙м | |||||||
| I2 | А |
По заданию требуется определить частоту вращения АД, соответствующую заданному моменту нагрузки на валу двигателя
MD = t∙MН.
Для этого определяем коэффициент нагрузки λD = MMAX / MD и скольжение sD, соответствующее этому моменту MD
sD = sКР / (λD + 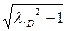 ),
),
и частоту вращения ротора АД
nD = n0∙(1- sD).
|
Рис. 2.2.







