Двумерная решетка представляет собой скрещенные перпендикулярно друг другу решетки с периодами 
и 
, причем часто 
. Пусть ось Х перпендикулярна щелям первой решетки. Ось Y – щелям второй, а ось Z направлена перпендикулярно плоскости двумерной решетки. Углы между падающими и дифрагированными лучами и осями Х, Y, Z обозначим, соответственно, через 
и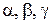 
. Очевидно, что 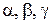- углы, дополняющие углы дифракции до 90о (рис. 10.1). Пусть на двумерную решетку нормально 
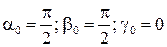падает плоская волна. Тогда условия возникновения главных максимумов для излучения с длиной волны l имеют вид:
(13.1)
Рис.13.1
Углы 
связаны между собой соотношением
(13.2)
Выражения (13.1) и (13.2) позволяют, при известных , и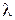 
, определить углы 
, 
, 
характеризующие направление дифрагированного луча для максимумов того или иного порядка. Если в каждой решетке число щелей N1 и N2 достаточно велико, то максимумы будут очень острыми и в них сосредоточится практически вся световая энергия дифрагировавших волн. В результате на экране, расположенном за двумерной решеткой получится дифракционная картина в виде четких, симметрично расположенных световых пятен, каждому из которых соответствуют два целочисленных индекса 
и 
(рис. 13.2).
Рис. 13.2
Главные максимумы возникают только тогда, когда 
и одновременно 
, где и целые числа. В этом случае интенсивность света в данном направлении 
. Если только одно из этих чисел ( или ) целое, т.е. выполняется условие возникновения главного максимума лишь для одной из решеток, то его интенсивность оказывается много меньше.
Одна система максимумов (соответствующая условию 
) располагается вдоль оси Х, а вторая (
) – вдоль оси Y. В центре картины находится максимум нулевого порядка, который лежит в направлении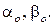 
Если углы дифракции малы, координаты главных максимумов вдоль оси Х и вдоль оси Y определятся соответственно как:
(13.3)
где 
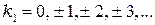и 
При больших расстояниях L от решетки до экрана, суперпозиция параллельных дифрагированных лучей осуществляется на экране и без собирающей линзы и выражения (13.3) примут вид:
(13.3а)
где 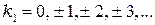и
Пусть волна падает на двумерную решетку наклонно (т.е. углы 
и 
отличны от 
). Тогда условия возникновения главных максимумов примут вид:
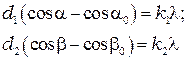
(13.4)
Общий характер дифракционной картины, в этом случае, останется прежним, изменятся лишь масштабы по осям Х и Y, наблюдаемой дифракционной картины.
Если решетки и взаимно не перпендикулярны, а составляют какой-либо угол между собой, положение максимумов будет зависеть от угла между штрихами решеток. Однако, нарушение строгой периодичности щелей (хаотическое их распределение) приводит к существенному изменению общей картины: наблюдаются симметричные размытые интерференционные кольца. Интенсивность наблюдаемых колец пропорциональна не квадрату числа щелей, а числу щелей. Таким образом, по расположению максимумов можно судить о величине периодов и и взаимной ориентации решеток.
