Дифракции Фраунгофера на нескольких щелях

Дифракционная решетка

 

Совокупность параллельных щелей называют дифракционной решёткой. Рассмотрим, для простоты, дифракцию от двух параллельных щелей одинаковой ширины и разделённых непрозрачным участком шириной 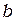. Дифракционная картина наблюдается в фокальной плоскости линзы Л (рис.11.1а). Пусть на экран со щелями падает плоская монохроматическая волна длиной 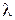. Положение дифракционных максимумов и минимумов от одной щели не зависит от её положения, а определяется направлением дифрагированных лучей. Это значит, что перемещение щели параллельно самой себе не приводит к изменению дифракционной картины. Следовательно, картины, создаваемые каждой щелью в отдельности будут совершенно одинаковыми.

Результирующую картину можно определить путем сложения этих двух дифракционных картин с учётом интерференции когерентных волн, идущих от каждой из щелей в соответствии с принципом Гюйгенса-Френеля. Очевидно, что в тех направлениях, в которых ни одна из щелей света не дает света, не будет света и при двух параллельных щелях. Условие минимума интенсивности (10.8) , где 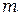= ±1, 2, 3,..., выполняется и в данном случае. Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, взаимно уничтожаются и возникают добавочные минимумы. Такие направления определяются условием минимума при интерференции – разность хода для таких волн равна не чётному числу полуволн:

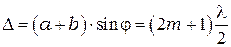(11.1)

где 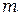= ± 0,1, 2, 3....

Л

 

Рис. 11.1

 

Таким образом, на дифракционной картине от двух щелей для минимумов возникают два характерных пространственных периода в плоскости экрана (рис.11.1б):

первый период - дифракционный (главный)

где 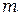= ± 0,1, 2, 3.... – число зон Френеля укладывающихся в щели шириной при угле дифракции ;

второй период - интерференционный (дополнительный)

(11.1а)

где 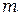= ± 0,1, 2, 3 – порядок минимума; 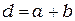- расстояние между центрами щелей. В первом случае, при синус угла, под которым наблюдается минимум, обратно пропорционален ширине щели (), во втором, – обратно пропорционален расстоянию между центрами щелей (рис. 11.1б). Так как 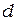всегда больше второй период всегда меньше, это значит, что интерференционные минимумы располагаются ближе к центру.

Вследствие той же интерференции в некоторых направлениях действие одной щели усиливает действие другой. Эти направления для волн определяются условием максимума интенсивности при интерференции – разность хода для них равна целому числу волн.

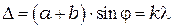(11.2)

Этим направлениям дифрагированных волн соответствуют максимумы интенсивности.

(11.2а)

где – порядок максимума, 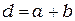- постоянная дифракционной решётки.

Расстояния между первичными (дифракционными) минимумами от одной щели зависит от ширины щели . Если , то между двумя первичными минимумами может расположиться несколько минимумов и максимумов. Кривая на рис. 11.1б показывает распределение интенсивностей света при дифракции на двух параллельных щелях.

Измерив на опыте по дифракционной картине от узкой щели ширину центрального максимума и зная длину волны источника света, можно определить ширину щели. По картине дифракции от двух параллельных узких щелей, зная длину волны источника и ширину каждой щели, можно определить расстояние между ними.

При увеличении числа щелей возникает случай многолучевой интерференции. При условии (11.2) векторы напряженности электрического поля всех N лучей на нормали АВ колеблются синфазно и при суперпозиции дают амплитуду результирующего колебания

которой соответствует интенсивность света:

(11.3а)

где I_j - интенсивность света при дифракции на одной щели (рис.10.1), определяемая формулой (10.6).

Более точный расчёт при дифракции на совокупности N щелей одинаковой ширины и одинакового расстоянии 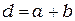между центрами щелей даёт выражение для интенсивности дифрагированных лучей в виде:

(11.3б)

где аргумент 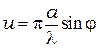, а аргумент 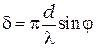; 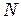- число щелей участвующих в дифракции; - интенсивность света в середине дифракционной картины (в направлении ).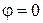

Формулу (11.3) можно представить в виде произведения двух членов. Первый член, называемый дифракционным, имеет вид:

. (11.4)

Вид этой функции показан рис. 11.1б штриховой линией.

Второй член, равный

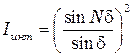, (11.5)

описывает интерференцию излучения, приходящего от различных щелей, и носит название интерференционного.

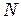Числитель в формуле (11.5) обращается в нуль при , однако для каждого -го значения в нуль обращается и знаменатель. Воспользовавшись предельным переходом, можно получить, что для этих значений угла функция (11.5) имеет одинаковое максимальное значение, равное . Таким образом, для этих значений угла интенсивность будет максимальной. Между этими максимумами, называемыми главными, располагаются (N- 1 ) добавочных минимумов, соответствующих нулевым значениям числителя в формуле (11.5). Так как между любыми двумя соседними добавочными минимумами имеется добавочный максимум, интенсивность которого существенно меньше интенсивности ближайших главных максимумов, то общее число добавочных максимумов между главными равно (N- 2 ).

Таким образом, получив на экране дифракционную картину от решетки и подсчитав число добавочных минимумов или максимумов между главными максимумами, можно определить число щелей решетки (когда число щелей не велико).

На рис. 11.2 показан ход лучей для дифракционной решётки, состоящей из трёх щелей (), для случая, когда разность хода волн от двух соседних щелей . В этом случае координата на экране Э соответствует главному максимуму первого порядка ().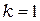

Так как между главными минимумами, например, первого порядка (), содержится не один, а несколько главных максимумов, то формула (11.4) характеризует «огибающую наибольших значений интенсивности света» этих нескольких главных максимумов, показанную на рис.11.2 пунктирной линией. Из формулы (11.5) видно, что дифракционная решетка позволяет резко (в раз) усилить интенсивность света в области максимумов по сравнению с картиной дифракции на одной щели.

 

Рис. 11.2. (а) - Ход лучей дифрагированного света от N щелей ();
(б) - Поперечное сечение распределения интенсивности света на экране

 

Главные максимумы разделены между собой не только главными минимума, но и рядом “дополнительных минимумов”, которые образуются вследствие интерференции N лучей при колебаниях вектора напряженности электрического поля в противофазе. Такие лучи гасят друг друга. Между «дополнительными минимумами» располагаются очень слабые «вторичные максимумы», число которых между соседними главными максимумами равно:

.

На рис.8.2 при числе щелей N = 3 число вторичных максимумов .

При в точке экрана против центра линзы расположен «центральный главный максимум». Симметрично относительно него расположены менее интенсивные главные максимумы высших порядков. Между главными минимумами первого порядка число главных максимумов

(11.12)

а между главными минимумами возрастающих порядков число главных максимумов

На рис.11.2 для отношения получено

Ширина главных максимумов зависит от числа N щелей, участвующих в дифракции, и определяется формулой

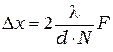(11.13)

Из сравнения формулы (10.11) ширины нулевого максимума для одиночной щели и формулы (11.13) видно, что (см. рис.8.2). При увеличения числа щелей ширина главных интерференционных максимумов уменьшается т.к. 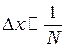, а интенсивность возрастает () (рис. 11.3)

Рис. 11.3

 

Таким образом, дифракционная решетка создает эффект резкого разделения и усиления максимумов интенсивности света.

При малых углах дифракции координаты минимумов или максимумов на экране наблюдения можно найти из геометрических соображений по приближённой формуле:

где - фокусное расстояние линзы. Отсюда и из условий (11.1а) и (11.2а) получим:

координаты главных минимумов для дифракционной решетки:

(11.14)

где - порядок минимума и

координаты главных максимумов для дифракционной решетки

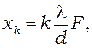(11.14а)

где 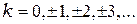- порядок максимума.

При больших расстояниях L от решетки до экрана суперпозиция (наложение) параллельных дифрагированных лучей осуществляется на экране и без собирающей линзы в точке , когда координаты главных минимумов и максимумов соответствуют формулам:

координаты главных минимумов для дифракционной решетки

(11.15)

где - порядок минимума и

координаты главных максимумов для дифракционной решетки

(11.15а)

где 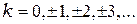- порядок максимума.

Дифракция на двух и на четырех щелях может рассматриваться как частный случай дифракции на решетке (N = 2 и N= 4 соответственно). При этом характер дифракционной картины соответствует рассмотренной на рис.11.2, где для дифракции на двух щелях

или ,

а для дифракции на четырех щелях

или .