В предыдущем параграфе мы имели дело с законами распределения случайных величин как с чем-то заранее известным. На практике, когда мы пытаемся систематизировать наблюдения и опытные данные и делать на основании этих наблюдений прогнозы, мы должны получить все характеристики из опытов. При этом следует иметь в виду, что всякий эксперимент связан с ошибками измерений и наблюдений, и значит, характеристики, полученные из опытов, являются лишь приближенными величинами. Следует убедиться в надежности полученных результатов (то есть знать вероятность того, что результаты измерений имеют заданную точность).
Разработка методов регистрации, описания и анализа статистических экспериментальных данных, полученных в результате наблюдения массовых случайных явлений, составляет предмет математической статистики. Основными задачами математической статистики являются 1) задача определения закона распределения случайной величины по статистическим данным, 2) задача выявления достоверности полученных параметров распределения, 3) задача проверки правдоподобия гипотезы о том, что случайная величина подчиняется выбранному закону распределения.
Для статистического анализа случайной величины мы производим выборку, то есть, измеряем не все значения случайной величины, а только часть случайно полученных значений. Тем более, что иногда опыт по измерению значений приводит к уничтожению объекта исследований. Так, измерение срока службы электрической лампочки имеет смысл только в том случае, если в итоге опыта лампочка придет в негодность. Предположим, что мы проводим анализ данных о росте трехлетних детей. При проведении опыта (измерении роста малышей) мы сначала записываем данные последовательно по мере их поступления (рост 1-го ребенка, рост 2-го ребенка,…). Следующий этап обработки статистических данных – построение статистической функции распределения исследуемой случайной величины. Статистической функцией распределения случайной величины 
называется частота события 
в полученном статистическом материале: 
. Здесь 
– это частота, то есть, отношение числа полученных в результате опыта значений случайной величины, меньших значения 
, к числу всех полученных значений. Мы получим неубывающую ступенчатую функцию, имеющую скачки в точках, соответствующих всем значениям случайной величины, полученным в результате опыта.
При увеличении числа опытов согласно закону больших чисел наша статистическая функция распределения приближается к подлинной функции распределения 
.
Аналогом закона распределения дискретной величины или плотности распределения непрерывной величины являются полигон частот и гистограмма частот.
Полигон частот мы получим, если каждому значению исследуемой величины, полученному в результате опыта, поставим в соответствие число наблюдений этого значения. Например, рост 1 м мы наблюдали у 7 детей, рост 1 м 1 см у 10 детей, рост
1м 2 см у 18 детей и т.д. На графике мы отложим значение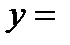 
7 при значении 
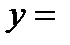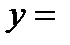100, значение 10 при значении 101, значение 18 при 102,… Соединив точки графика отрезками прямых, мы получим многоугольник, который и называют полигоном частот. В случае, когда по вертикали мы откладываем не число наблюдений данного
значения, а отношение этого числа к числу всех измерений, мы получим полигон относительных частот.
В том случае, когда число данных, полученных в результате опыта, очень велико и расположены эти данные близко друг к другу, то есть случайная величина распределена практически непрерывно, прибегают к построению гистограммы. В отличие от полигона частот при построении гистограммы на оси отмечают не отдельные значения, которые принимает случайная величина, а равные интервалы значений, а над каждым таким интервалом на высоте, равной количеству наблюденных значений случайной величины, попавших в этот интервал, помещают параллельный оси отрезок.
Аналогом математического ожидания случайной величины при статистической обработке является среднее арифметическое полученных значений 
, называемое эмпирическим математическим ожиданием или средним по выборке. Здесь 
– количество измерений, 
– наблюдаемое значение случайной величины при 
-м измерении. Аналогом дисперсии случайной величины при статистической обработке является эмпирическая дисперсия, вычисляемая по формуле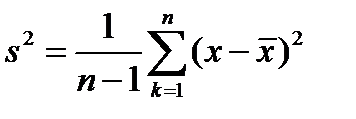 
. Замена 
на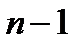 
в знаменателе неслучайна, но объяснение этого не входит в нашу программу, поэтому ограничимся замечанием, что при больших значениях такая замена несущественна.
После определения эмпирических параметров встает вопрос о точности оценок параметров выбранного распределения. Предположим, что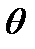 
– интересующий нас параметр распределения. На основании выборки находится интервал 
, в котором может находиться параметр и оценивается вероятность 
. Если получена такая оценка 
, то интервал называется доверительным интервалом для параметра 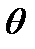, а число 
называется надежностью сделанной оценки. Если надежность попадания в предложенный интервал достаточно высока (например, больше 95%), за значение 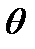берут середину доверительного интервала (
).
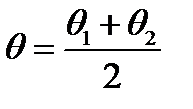Пример. Пусть нам нужно найтидоверительный интервал для математического ожидания нормального распределения случайной величины 
при известной дисперсии 
. В результате опыта мы получили значения 
случайной величиныи нашли эмпирическое математическое ожидание 
. Мы хотим исследовать разность между этим эмпирическим математическим ожиданием и реальным неизвестным нам математическим ожиданием 
.
Считая, что каждое значение, полученное в результате измерения – это тоже случайная величина, не зависимая от других измерений, распределенная по тому же закону, что и , мы можем рассматривать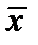 
как случайную величину, распределенную по нормальному закону (из свойств нормального распределения). Математическим ожиданием случайной величины 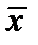будет , а дисперсией 
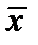.Значит, функцией распределения случайной величины будет 
. Следовательно,
Задав надежность 
, мы по таблицам для функции 
найдем то значение аргумента, при котором эта функция имеет значение 
. Теперь остается приравнять полученное значение аргумента выражению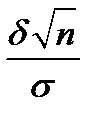 
и найти длину доверительного интервала 
.
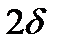Итак, мы получили параметры и выбрали подходящий закон распределения с этими параметрами. Теперь на основании полученного статистического материала нам предстоит проверить гипотезу, состоящую в том, что исследуемая случайная величина подчиняется конкретному закону распределения, например, имеет функцию распределения 
. Для проверки гипотезы существуют специальные критерии, позволяющие найти вероятность того, что отклонения данных, полученных в результате измерений, от данных, получаемых в соответствии с использованием гипотезы, вызваны случайными причинами. Если такая вероятность мала, гипотезу отвергают, если велика, гипотезу принимают.
Задания.
1. Построить полигон частот по данному распределению выборки:
а)
| ||||
|
б)
|
| |||||
|
|
2. Построить полигоны частот распределения.
|
| |||||
|
|
Найти среднее.
3. Построить гистограммы частот распределения (в первом столбце указан частичный интервал, во втором – сумма частот вариант частичного интервала).
а) 2 – 5 9 б) 150 – 155 3
5 – 8 10 155 – 160 5
8 – 11 25 160 – 165 8
11 – 14 6; 165 – 170 6
170 – 175 2
4. Дана выборка: 3, 1, 2, 1, 0, 4, 1, 4, 5, 6, 2, 5, 1, 0, 2, 3, 3, 3, 0,1.
1) Составить таблицы частот и относительных частот;
2) Построить полигоны частот и относительных частот;
3) Вычислить среднее;
4) Составить интервальные таблицы частот и относительных частот с шагом h = 2;
5) Построить гистограмму.
5. Найти доверительный интервал для оценки с надежностью 
неизвестного математического ожидания m нормально распределенного признака Х генеральной совокупности, если известны генеральное квадратическое отклонение 
выборочная средняя 
и объем выборки: а) 
; б) 
6. Из генеральной совокупности извлечена выборка объема n = 10:
хi: -2 1 2 3 4 5
ni 2 1 2 2 2 1
Оценить с надежностью 
математическое ожидание m нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
В конце пособия мы помещаем таблицу удвоенной функции Лапласа.
Таблица удвоенной функции Лапласа
| 
|
|
|
|
|
|
|
|
|
|
|
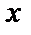
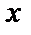
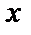
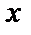
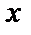
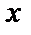
| 0.00 | 0.00000 | 0.36 | 0.28115 | 0.73 | 0.53461 | 1.10 | 0.72867 | 1.47 | 0.85844 | 1.84 | 0.93423 |
| 0.01 | 0.00798 | 0.37 | 0.28862 | 0.74 | 0.54070 | 1.11 | 0.73300 | 1.48 | 0.86113 | 1.85 | 0.93569 |
| 0.02 | 0.01596 | 0.38 | 0.29605 | 0.75 | 0.54675 | 1.12 | 0.73729 | 1.49 | 0.86378 | 1.86 | 0.93711 |
| 0.03 | 0.02393 | 0.39 | 0.30346 | 0.76 | 0.55275 | 1.13 | 0.74152 | 1.50 | 0.86639 | 1.87 | 0.93852 |
| 0.04 | 0.03191 | 0.40 | 0.31084 | 0.77 | 0.55870 | 1.14 | 0.74571 | 1.51 | 0.86696 | 1.88 | 0.93989 |
| 0.05 | 0.03988 | 0.41 | 0.31819 | 0.78 | 0.56461 | 1.15 | 0.74986 | 1.52 | 0.87149 | 1.89 | 0.94124 |
| 0.06 | 0.04784 | 0.42 | 0.32552 | 0.79 | 0.57047 | 1.16 | 0.75395 | 1.53 | 0.87398 | 1.90 | 0.94257 |
| 0.07 | 0.05581 | 0.43 | 0.33280 | 0.80 | 0.57629 | 1.17 | 0.75800 | 1.54 | 0.87644 | 1.91 | 0.94387 |
| 0.08 | 0.06376 | 0.44 | 0.34006 | 0.81 | 0.58206 | 1.18 | 0.76200 | 1.55 | 0.87886 | 1.92 | 0.94514 |
| 0.09 | 0.07171 | 0.45 | 0.34729 | 0.82 | 0.58778 | 1.19 | 0.76595 | 1.56 | 0.88124 | 1.93 | 0.94639 |
| 0.10 | 0.07966 | 0.46 | 0.35448 | 0.83 | 0.59346 | 1.20 | 0.76986 | 1.57 | 0.88358 | 1.94 | 0.94762 |
| 0.11 | 0.08759 | 0.47 | 0.36164 | 0.84 | 0.59909 | 1.21 | 0.77372 | 1.58 | 0.88589 | 1.95 | 0.94882 |
| 0.12 | 0.09552 | 0.48 | 0.36877 | 0.85 | 0.60468 | 1.22 | 0.77754 | 1.59 | 0.88817 | 1.96 | 0.95000 |
| 0.13 | 0.10348 | 0.49 | 0.37587 | 0.86 | 0.61021 | 1.23 | 0.78130 | 1.60 | 0.89040 | 1.97 | 0.95116 |
| 0.14 | 0.11134 | 0.50 | 0.38292 | 0.87 | 0.61570 | 1.24 | 0.78502 | 1.61 | 0.89260 | 1.98 | 0.95230 |
| 0.15 | 0.11924 | 0.51 | 0.38995 | 0.88 | 0.62114 | 1.25 | 0.78870 | 1.62 | 0.89477 | 1.99 | 0.95341 |
| 0.16 | 0.12712 | 0.52 | 0.39694 | 0.89 | 0.62653 | 1.26 | 0.79233 | 1.63 | 0.89690 | 2.00 | 0.95450 |
| 0.17 | 0.13499 | 0.53 | 0.40389 | 0.90 | 0.63188 | 1.27 | 0.79592 | 1.64 | 0.89899 | 2.01 | 0.95557 |
| 0.18 | 0.14285 | 0.54 | 0.41080 | 0.91 | 0.63718 | 1.28 | 0.79945 | 1.65 | 0.90106 | 2.02 | 0.95662 |
| 0.19 | 0.15069 | 0.55 | 0.41768 | 0.92 | 0.64243 | 1.29 | 0.80295 | 1.66 | 0.90309 | 2.03 | 0.95764 |
| 0.20 | 0.15852 | 0.56 | 0.42452 | 0.93 | 0.64763 | 1.30 | 0.80640 | 1.67 | 0.90508 | 2.04 | 0.95865 |
| 0.21 | 0.16633 | 0.57 | 0.43132 | 0.94 | 0.65278 | 1.31 | 0.80980 | 1.68 | 0.90704 | 2.05 | 0.95964 |
| 0.22 | 0.17413 | 0.58 | 0.43809 | 0.95 | 0.65789 | 1.32 | 0.81316 | 1.69 | 0.90897 | 2.06 | 0.96060 |
| 0.23 | 0.18191 | 0.59 | 0.44481 | 0.96 | 0.66294 | 1.33 | 0.81648 | 1.70 | 0.91087 | 2.07 | 0.96155 |
| 0.24 | 0.18967 | 0.60 | 0.45149 | 0.97 | 0.66795 | 1.34 | 0.81975 | 1.71 | 0.91273 | 2.08 | 0.96247 |
| 0.25 | 0.19741 | 0.61 | 0.45814 | 0.98 | 0.67291 | 1.35 | 0.82298 | 1.72 | 0.91457 | 2.09 | 0.96338 |
| 0.26 | 0.20514 | 0.62 | 0.46474 | 0.99 | 0.67783 | 1.36 | 0.82617 | 1.73 | 0.91637 | 2.10 | 0.96427 |
| 0.27 | 0.21284 | 0.63 | 0.47131 | 1.00 | 0.68269 | 1.37 | 0.82931 | 1.74 | 0.91814 | 2.11 | 0.96514 |
| 0.28 | 0.22052 | 0.64 | 0.47783 | 1.01 | 0.68750 | 1.38 | 0.83241 | 1.75 | 0.91988 | 2.12 | 0.96599 |
| 0.29 | 0.22818 | 0.65 | 0.48431 | 1.02 | 0.69227 | 1.39 | 0.83547 | 1.76 | 0.92159 | 2.13 | 0.96683 |
| 0.30 | 0.23582 | 0.66 | 0.49075 | 1.03 | 0.69699 | 1.40 | 0.83849 | 1.77 | 0.92327 | 2.14 | 0.96765 |
| 0.31 | 0.24344 | 0.67 | 0.49714 | 1.04 | 0.70166 | 1.41 | 0.84146 | 1.78 | 0.92492 | 2.15 | 0.96844 |
| 0.32 | 0.25103 | 0.68 | 0.50350 | 1.05 | 0.70628 | 1.42 | 0.84439 | 1.79 | 0.92655 | 2.16 | 0.96923 |
| 0.33 | 0.25860 | 0.69 | 0.50981 | 1.06 | 0.71086 | 1.43 | 0.84728 | 1.80 | 0.92814 | 2.17 | 0.96999 |
| 0.34 | 0.26614 | 0.70 | 0.51607 | 1.07 | 0.71538 | 1.44 | 0.85013 | 1.81 | 0.92970 | 2.18 | 0.97074 |
| 0.35 | 0.27366 | 0.71 | 0.52230 | 1.08 | 0.71986 | 1.45 | 0.85294 | 1.82 | 0.93124 | 2.19 | 0.97148 |
| 0.72 | 0.52848 | 1.09 | 0.72429 | 1.46 | 0.85571 | 1.83 | 0.93275 | 2.20 | 0.97219 |
Литература
1. Математика: Учебно-методическое пособие / М.С.Малакаев, Е.А. Широкова – Казань: Казанский федеральный университет, 2011. – 140 с.
2. Математика: Учебно-методическое пособие / Н.Р. Абубакиров, М.С.
Малакаев. – Казань: Казанский федеральный университет, 2010. – 72 с.
Электронные ресурсы
1.http://festival.1september.ru/articles/416943/
2.http://matmetod-popova.narod.ru/theme213.htm
