Выше было показано, что если ограничения ЗЛП содержат единичную матрицу порядка m или приводятся к такому виду, то тем самым при неотрицательных правых частях уравнений определен первоначальный план, исходя из которого, симплексным методом, находится оптимальный план. В частности, если ограничения ЗЛП можно преобразовать к виду АX£A0 при А0³0, то система ограничений всегда содержит единичную матрицу. Если же ЗЛП, имеющая решения, не содержит единичную матрицу и не приводится к указанному виду, то для решения применяется метод искусственного базиса.
Найдем минимальное значение функции L=С1x1+С2x2+…+Сnxn при ограничениях
.
причем xj ³ 0 j=1,2,..,n; bi ³ 0, i=1,2,…,m, и система ограничений не содержит единичную матрицу.
Для получения единичной матрицы в каждое уравнение вводим по одной вспомогательной переменной y1,y2,...,ym с коэффициентом +1, называемой искусственной. В целевую функцию в задаче на максимум искусственная переменная войдет с коэффициентом –М, а в задаче на минимум с коэффициентом +М. Число М сколь угодно большое по сравнению с единицей (М>>1). Выражение М(y1+…+ym) назовем М-функцией.
Тогда рассмотрим расширенную задачу, связанную с отысканием наименьшего значения новой линейной функции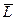 
=L+М(y1+…+ym)=С1x1+С2x2+…+Сnxn+Мy1+…+Мym при ограничениях:
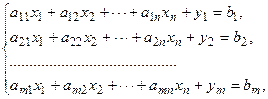(1)
Единичные векторы Аn+1,…,An+m, соответствующие искусственным переменным, образуют искусственный базис:
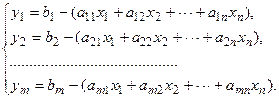(2)
Тогда в целевой функции 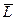в расширенной задаче при коэффициенте М вместо переменных yi подставляем их выражения из (2).
Очевидно, что решение исходной системы (1) эквивалентно решению системы (2) при равенстве нулю дополнительных переменных y1=0, y2=0,...,ym=0.
Для отыскания оптимального плана исходной задачи используют следующую теорему.
Теорема.
1. Если в оптимальном решении расширенной задачи при нахождении минимума 
=(x*1,x*2,…,x*n,0,…0) все искусственные переменные yi=0 (i=1,2,…,m), то решение Х*=(x*1,x*2,…,x*n) является оптимальным решением исходной задачи.
2. Если оптимальное решение расширенной задачи содержит, по крайней мере, одну искусственную переменную yi>0, то исходная задача не имеет решения (т.е. она не совместна).
3. Если 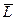max=µ, то исходная задача также неразрешима, причем либо L max=µ, либо условия задачи противоречивы.
Доказательство. Докажем первую часть теоремы, остальные пункты примем без доказательства.
Заметим, что если решение - оптимальное решение расширенной задачи, то решение Х* - решение исходной задачи, при этом 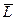()=L(X*). Равенство значений функции следует из того, что решение от решение Х* отличается m последними компонентами, равными нулю.
Докажем, что план Х* - оптимальное решение исходной задачи. Предположим противное, допустим, что Х* не является оптимальным решением. Тогда существует такое оптимальное решение Х=(x1,x2,…,xn), для которого L(X)<L(X*). Отсюда для вектора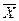 
=(x1,x2,…,xn,0,…0), являющегося решением расширенной задачи, получим
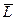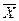()= L(X)<L(X*)= (),
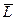т.е.
() < (),
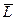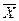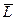что противоречит условию задачи о том, что - оптимальное решение расширенной задачи.¨
Из теоремы следует, что вначале следует найти оптимум М-функции. Если он равен 0 и все искусственные переменные yi=0, то далее их можно отбросить и решать исходную задачу, исходя их полученного допустимого базисного решения. На практике находят оптимум (- М)-функции.
Метод искусственного базиса в основном совпадает с обычным симплексным методом, но имеет некоторые особенности:
1. Ввиду того, что первоначальный опорный план расширенной задачи содержит искусственные переменные, входящие в целевую функцию с коэффициентом –М (в задаче на максимум), с коэффициентом +М (в задаче на минимум), то симплексные таблицы имеют на одну строку больше, чем обычные таблицы. В (m+1)-ю строку записываем коэффициенты слагаемых целевой функции расширенной задачи, независящие от М, в (m+2)-ю - зависящие от М. Таким образом, последняя строка – это (- М)-функция. Из теоремы следует, что вначале следует найти оптимум М-функции.
2. Соответствующие искусственным переменным вектора, выводимые из базиса опорного решения, в дальнейшем исключаются из рассмотрения.
3. После того как все векторы, соответствующие искусственным переменным, исключаются из базиса, расчет продолжается обычным симплексным методом по виду коэффициентов (m+1)-ой строки.
Пример. L=x1+2x2 ®max при ограничениях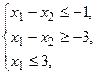 
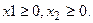
Умножим 1-е и 2-е неравенство на (-1), получим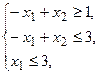 
Приведем систему ограничений к канонической форме, имеем 
Прежде всего, замечаем, что, например, x4 и x5 входят только во 2-е и 3-е уравнения соответственно, причем коэффициенты при них имеют тот же знак, что и свободные члены. Поэтому можем объявить их базисными переменными. Тогда чтобы получить первоначальный опорный план, в 1-ое уравнение введем искусственную переменную y1:
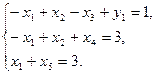Тогда базисные переменные: 
Линейная функция расширенной задачи 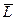= x1+2x2-Мy1=x1+2x2-М(x1-x2+х3)®max
Первоначальный опорный план 1=(0;0;0;3;3;1).
Составляем 1-ую симплексную таблицу.
| Базис | Свобод. | переменные | Оценочное | |||||
| член А0 | x1 | X2 | х3 | x4 | x5 | Y1 | Отношение | |
 Y1
| -1 | -1 | ||||||
| Х4 | -1 | |||||||
| x5 | µ | |||||||
| L | -1 | -2 | Max | |||||
| Mф | -1 | Max |
В (m+1)-ю строку записываем слагаемые, независящие от М, в (m+2)-ю - зависящие от М. Проверяя выполнения критерия оптимальности при отыскании максимума (-М)-функции, определяем, что в последней строке имеется отрицательный элемент во 2-ом столбце, значит он разрешающий, х2 переходит в базисные. Минимальное оценочное отношение в 1-ой строке, она разрешающая. Переменная y1 переходит в свободные, обращается в 0 на следующем базисном решении и далее исключается из рассмотрения. Получаем новую таблицу 2.
Таблица 2.
| Базис | Свобод. |  переменные
| Оценочное | ||||
| член А0 | x1 | x2 | х3 | x4 | x5 | отношение | |
| х2 | -1 | -1 | |||||
| х4 | |||||||
 х5
| |||||||
| L | -3 | -2 | Max | ||||
| -Mф | Max |
Последняя строка показывает, что критерий оптимальности выполнен;
max(-Мф)=0, далее эту строку можно не рассматривать. Получено допустимое базисное решение 2= (0; 1; 0; 2; 3;0), начиная с которого решаем исходную задачу в соответствии с обычным алгоритмом.
Таблица 3.
| Базис | Свобод. |  переменные
| Оценочное | ||||
| член А0 | x1 | x2 | х3 | x4 | X5 | Отношение | |
| х2 | -1 | µ | |||||
| х4 |  2
| 2/1 | |||||
| х1 | -1 | µ | |||||
| L | -2 |
3= (3; 4; 0; 2; 3)
Таблица 4.
| Базис | Свобод. | Переменные | Оценочное | ||||
| член А0 | x1 | x2 | х3 | x4 | x5 | Отношение | |
| х2 | |||||||
| х3 | |||||||
| х1 | |||||||
| L |
Получаем следующее опорное решение 4= (3; 6; 2; 0; 0), которое является оптимальным решением расширенной задачи, т.к. оценки для всех векторов положительные. Исходная задача имеет оптимальное решение, которое получается отбрасыванием нулевых дополнительных и искусственной переменных. X*=(3;6) Lmax=15.
Контрольные вопросы
1. Геометрическая интерпретация симплексного метода.
2. Построение первоначального опорного плана.
3. Критерии оптимальности решения задач линейного программирования симплексным методом.
4. Табличный вариант реализации симплексного метода.
Рекомендованная литература: [ 1, 5, 6, 7]
